Question: Prove each identity, assuming that S and
Prove each identity, assuming that S and E satisfy the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second-order partial derivatives.
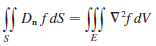
Transcribed Image Text:
Sſ Da f ds = {[[ v?fav v²fdV E
> Use power series to solve the differential equation. y'' + x2y = 0, y (0) = 1, y'(0) = 0
> Use power series to solve the differential equation. y'' – xy' - y = 0, y (0) = 1, y' (0) = 0
> Use power series to solve the differential equation. y'' = xy
> Use power series to solve the differential equation. (x – 1) y' + y' = 0
> Use power series to solve the differential equation. y'' = y
> Use Stokes’ Theorem to evaluate ∫C F ∙ dr, where F (x, y, z) = xy i + yz j + z x k, and C is the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1), oriented counterclockwise as viewed from above.
> Use power series to solve the differential equation. y'' + xy' + y = 0
> Use power series to solve the differential equation. (x – 3) y' + 2y = 0
> Use power series to solve the differential equation. y' = x2y
> Solve the differential equation. Y'' - 6y' + 9y = 0
> Use power series to solve the differential equation. y' – y = 0
> How do you find the cross product a × b of two vectors if you know their lengths and the angle between them? What if you know their components?
> Write expressions for the scalar and vector projections of b onto a. Illustrate with diagrams.
> How do you find the dot product a ∙ b of two vectors if you know their lengths and the angle between them? What if you know their components?
> How do you find the vector from one point to another?
> How do you add two vectors geometrically? How do you add them algebraically?
> Use Stokes’ Theorem to evaluate ∫∫S curl F ∙ dS, where F (x, y, z) = x2yz i + yz2 j + z3exy k, S is the part of the sphere x2 + y2 + z2 = 5 that lies above the plane z = 1, and S is oriented upward.
> Write equations in standard form of the six types of quadric surfaces.
> How do you find the angle between two intersecting planes?
> (a). How do you find the area of the parallelogram determined by a and b? (b). How do you find the volume of the parallelepiped determined by a, b, and c?
> What is the difference between a vector and a scalar?
> Solve the differential equation. y'' - 4y' + 13y = 0
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. y" – y = xe2", y(0) = 0, y'(0) = 1
> Solve the differential equation. 3y'' = 4y'
> For the spring in Exercise 4, find the damping constant that would produce critical damping. Exercise 4: A force of 13 N is needed to keep a spring with a 2-kg mass stretched 0.25 m beyond its natural length. The damping constant of the spring is c = 8
> For the spring in Exercise 3, find the mass that would produce critical damping. Exercise 3: A spring with a mass of 2 kg has damping constant 14, and a force of 6 N is required to keep the spring stretched 0.5 m beyond its natural length. The spring i
> A force of 13 N is needed to keep a spring with a 2-kg mass stretched 0.25 m beyond its natural length. The damping constant of the spring is c = 8. (a). If the mass starts at the equilibrium position with a velocity of 0.5 m/s, find its position at time
> Verify that Stokes’ Theorem is true for the vector field F (x, y, z) = x2 i + y2 j + z2 k, where S is the part of the paraboloid z = 1 - x2 - y2 that lies above the xy-plane and S has upward orientation.
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. 9y" + y = e2*
> Consider a spring subject to a frictional or damping force. (a). In the critically damped case, the motion is given by x = c1ert + c2tert. Show that the graph of x crosses the t-axis whenever c1 and c2 have opposite signs. (b). In the overdamped case, th
> Solve the differential equation. 2 d2y/dt2 + 2 dy/dt - y = 0
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. y" + y' – 2y = x + sin 2x, y(0) = 1, y'(0) = 0 %3D
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. y'' + 2y' - 8y = 1 - 2x2
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — 4y' + 4у %3х — sin x
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — 4у' + 5у — е*
> Solve the differential equation or initial-value problem using the method of undetermined coefficients. у" — 2у' + 2у х+e*
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. у" + 2y' + 10у 3D х?е-* сos 3x
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. y" + 3y' – 4y = (x³ + x)e*
> Evaluate the surface integral. ∫∫S F ∙ dS, where F (x, y, z) = x2 i + xy j + z k and S is the part of the paraboloid z = x2 + y2 below the plane z = 1 with upward orientation
> (a). Write the general form of a second-order nonhomogeneous linear differential equation with constant coefficients. (b). What is the complementary equation? How does it help solve the original differential equation? (c). Explain how the method of undet
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. у" — Зу' + 2у — е* + sin x
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. y" + 4y = cos 4x + cos 2x %3D COS
> Write a trial solution for the method of undetermined coefficients. Do not determine the coefficients. y" – y' – 2y = xe*cos x
> Solve the differential equation. d2R /dt2 + 6 dR/dt + 34R = 0
> Solve the differential equation. y = y''
> Solve the differential equation. 9y'' + 4y = 0
> Solve the differential equation. 4y'' + 4y' + y = 0
> Solve the differential equation. y'' + y' - 12y = 0
> Solve the differential equation. y'' + 2y = 0
> Evaluate the surface integral. ∫∫S F ∙ dS, where F (x, y, z) = xz i - 2y j + 3x k and S is the sphere x2 + y2 + z2 = 4 with outward orientation
> Prove each identity, assuming that S and E satisfy the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second-order partial derivatives. curl F· dS = 0
> Solve the boundary-value problem, if possible. y'' + 6y' = 0, y (0) = 1, y (1) = 0
> Prove each identity, assuming that S and E satisfy the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second-order partial derivatives. || a·n ds = 0, where a is a constant vector %3
> Solve the initial-value problem. 4y'' + 4y' + 3y = 0, y (0) = 0, y' (0) = 1
> Solve the initial-value problem. y'' – y' - 12y = 0, y (1) = 0, y' (1) = 1
> Solve the initial-value problem. 3y'' - 2y' - y = 0, y (0) = 0, y' (0) = -4
> Solve the initial-value problem. 9y'' + 12y' + 4y = 0, y (0) = 1, y' (0) = 0
> Solve the initial-value problem. y'' - 2y' - 3y = 0, y (0) = 2, y'(0) = 2
> Solve the initial-value problem. y'' + 3 = 0, y (0) = 1, y' (0) = 3
> Use a computer algebra system to plot the vector field F (x, y, z) = sin x cos2y i + sin3y cos4z j + sin5z cos6x k in the cube cut from the first octant by the planes x = π/2, y = π/2, and z = π/2. Then compute the flux across the surface of the cube.
> Evaluate the surface integral. ∫∫S (x2z + y2z) dS, where S is the part of the plane z = 4 + x + y that lies inside the cylinder x2 + y2 = 4
> Use the Divergence Theorem to calculate the surface integral ∫∫S F dS; that is, calculate the flux of F across S. F (x, y, z) = ey tan z i + y√3 - x2 j + x sin y k, S is the surface of the solid that lies above the xy-plane and below the surface z = 2
> Use the Divergence Theorem to calculate the surface integral ∫∫S F dS; that is, calculate the flux of F across S. F = |r |2 r, where r = x i + y j + z k, S is the sphere with radius R and center the origin
> Solve the differential equation. 3 d2V/dt2 + 4 dV/dt + 3V = 0
> The vector field F is shown in the xy-plane and looks the same in all other horizontal planes. (In other words, F is independent of z and its z-component is 0.) (a). Is div F positive, negative, or zero? Explain. (b). Determine whether curl F = 0. If n
> Define the linearization of f at (a, b). What is the corresponding linear approximation? What is the geometric interpretation of the linear approximation?
> (a). Write the definition of the triple integral of f over a rectangular box B. (b). How do you evaluate ∫∫∫B f (x, y, z) dV? (c). How do you define ∫∫∫B f (x, y, z) dV if E is a bounded solid region that is not a box? (d). What is a type 1 solid region?
> What is a function of three variables? How can you visualize such a function?
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = y2exy i + (1 + xy) exy j
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (y2 - 2x) i + 2xy j
> How do you change from rectangular coordinates to polar coordinates in a double integral? Why would you want to make the change?
> Evaluate the surface integral. ∫∫S z dS, where S is the part of the paraboloid z = x2 + y2 that lies under the plane z = 4
> (a). How do you define ∫∫D f (x, y) dA if D is a bounded region that is not a rectangle? (b). What is a type I region? How do you evaluate ∫∫D f (x, y) dA if D is a type I region? (c). What is a type II region? How do you evaluate ∫∫D f (x, y) dA if D is
> The figure shows a curve C and a contour map of a function f whose gradient is continuous. Find ∫C ∇f dr. yA 60 50 40 C 30 20 10
> What does lim (x, y) → (a, b) f (x, y) = L mean? How can you show that such a limit does not exist?
> If F is the vector field of Example 5, show that ∫C F ∙ dr = 0 for every simple closed path that does not pass through or enclose the origin.
> (a). What is a closed set in R2? What is a bounded set? (b). State the Extreme Value Theorem for functions of two variables. (c). How do you find the values that the Extreme Value Theorem guarantees?
> State the Second Derivatives Test.
> (a). If f has a local maximum at (a, b), what can you say about its partial derivatives at (a, b)? (b). What is a critical point of f?
> (a). Write an expression as a limit for the directional derivative of f at (x0, y0) in the direction of a unit vector u =〈a, b〉. How do you interpret it as a rate? How do you interpret it geometrically? (b). If f is differentiable, write an expression fo
> Match the vector fields F with the plots labeled I–IV. Give reasons for your choices. F (x, y) = 〈y, x - y〉 3 -3 -3 en
> The figure shows the vector field F (x, y) = 〈2xy, x2〉 and three curves that start at (1, 2) and end at (3, 2). (a). Explain why ∫C F ∙ dr has the same value for all three curves.
> (a). Find an equation of the tangent plane at the point (4, -2, 1) to the parametric surface S given by (b). Use a computer to graph the surface S and the tangent plane found in part (a). (c). Set up, but do not evaluate, an integral for the surface a
> (a). If a transformation T is given by x = g (u, v), y = h (u, v), what is the Jacobian of T? (b). How do you change variables in a double integral? (c). How do you change variables in a triple integral?
> (a). How do you change from rectangular coordinates to cylindrical coordinates in a triple integral? (b). How do you change from rectangular coordinates to spherical coordinates in a triple integral? (c). In what situations would you change to cylindrica
> Determine whether or not the given set is (a) open, (b) connected, and (c) simply-connected. {(x, y) | 0 < y < 3}
> Match the functions f with the plots of their gradient vector fields labeled I–IV. Give reasons for your choices. f (x, y) = x2 + y2 4 -4 -4 4.
> If F (x, y) = sin y i + (1 + x cos y) j, use a plot to guess whether F is conservative. Then determine whether your guess is correct.
> (a). Write formulas for the unit normal and binormal vectors of a smooth space curve r (t). (b). What is the normal plane of a curve at a point? What is the osculating plane? What is the osculating circle?
> Explain how the method of Lagrange multipliers works in finding the extreme values of f (x, y, z) subject to the constraint g (x, y, z) = k. What if there is a second constraint h (x, y, z) = c?
> What do the following statements mean? (a). f has a local maximum at (a, b). (b). f has an absolute maximum at (a, b). (c). f has a local minimum at (a, b). (d). f has an absolute minimum at (a, b). (e). f has a saddle point at (a, b).
> (a). Sketch the vector field F (x, y) = i + x j and then sketch some flow lines. What shape do these flow lines appear to have? (b). If parametric equations of the flow lines are x = x (t), y = y (t), what differential equations do these functions satisf
> The flow lines (or streamlines) of a vector field are the paths followed by a particle whose velocity field is the given vector field. Thus, the vectors in a vector field are tangent to the flow lines. (a). Use a sketch of the vector field F (x, y) = x i
> Find the positively oriented simple closed curve C for which the value of the line integral ∫C (y3 – y) dx - 2x3 dy is a maximum.
> At time t = 1, a particle is located at position (1, 3). If it moves in a velocity field F (x, y) = 〈xy - 2, y^2 - 10〉 find its approximate location at time t = 1.05.
> Find the area of the part of the sphere x2 + y2 + z2 = a2 that lies inside the cylinder x2 + y2 = ax.
> The figure shows the surface created when the cylinder y2 + z2 = 1 intersects the cylinder x2 + z2 = 1. Find the area of this surface. ZA x- y
> Find the area of the part of the sphere x2 + y2 + z2 = 4z that lies inside the paraboloid z = x2 + y2.
> Match the functions f with the plots of their gradient vector fields labeled I–IV. Give reasons for your choices. f (x, y) = x (x + y) II 4 -4 4 -4
> (a). Show that the parametric equations x = a sin u cos v, y = b sin u sin v, z = c cos u, 0 < u

