Question: Prove (Theorem 2.3) that / for
Prove (Theorem 2.3) that
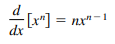
for the case in which n is a rational number. (Hint: Write y = xp/q in the form yq = xp and differentiate implicitly. Assume that p and q are integers, where q > 0.)
> f(x) = x3 − 2x + 3x−3 Find the derivative of the function.
> f(x) = x2 + 5 − 3x−2 Find the derivative of the function
> Function: g(t) = −2 cos t + 5 Point: (π, 7) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: f(θ) = 4 sin θ − θ. Point: (0, 0 )
> f(x) = x(2x - 5)3 Find the derivative of the function.
> Function: f(x) = 2(x − 4)2 Point: (2, 8) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Function: y = 2x4 − 3 Point: (1, -1) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point:
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point: (4, 1)
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point: (2,2)
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> f(x) = x2 (x - 2)7 Find the derivative of the function.
> y = 7x4 + 2 sin x Use the rules of differentiation to find the derivative of the function.
> y = x2 – ½ cos. Use the rules of differentiation to find the derivative of the function.
> g(t) = π cos t Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> y = 2x3 + 6x2 − 1 Use the rules of differentiation to find the derivative of the function.
> s(t) = t 3 + 5t 2 − 3t + 8 Use the rules of differentiation to find the derivative of the function.
> y = 4x − 3x3 Use the rules of differentiation to find the derivative of the function.
> g(x) = x2 + 4x3 Use the rules of differentiation to find the derivative of the function.
> y = t 2 − 3t + 1 Use the rules of differentiation to find the derivative of the function.
> f(t) = −3t 2 + 2t − 4 Use the rules of differentiation to find the derivative of the function.
> Find the derivative of the function.
> g(x) = 6x + 3 Use the rules of differentiation to find the derivative of the function.
> f(x) = x + 11 Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function. /
> Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> y = x12 Use the rules of differentiation to find the derivative of the function.
> y = x7 Use the rules of differentiation to find the derivative of the function.
> f(x) = −9 Use the rules of differentiation to find the derivative of the function.
> y = 12 Use the rules of differentiation to find the derivative of the function.
> Find the derivative of the function.
> Use the graph to estimate the slope of the tangent line to y = xn at the point (1, 1). Verify your answer analytically. To print an enlarged copy of the graph, go to MathGraphs.com. (a) y = x−1/2 (b) y = x−1
> Use the graph to estimate the slope of the tangent line to y = xn at the point (1, 1). Verify your answer analytically. To print an enlarged copy of the graph, go to MathGraphs.com (a) y = x1/2 (b) y = x3
> Describe the difference between average velocity and velocity.
> What are the derivatives of the sine and cosine functions?
> Explain how to find the derivative of the function f(x) = cxn.
> What is the derivative of a constant function?
> (a)Find an equation of the normal line to the ellipse x2/32 + y2/8 = 1 at the point (4, 2). (b) Use a graphing utility to graph the ellipse and the normal line. (c) At what other point does the normal line intersect the ellipse?
> The graph shows the normal lines from the point (2, 0) to the graph of the parabola x = y2. How many normal lines are there from the point (x0, 0) to the graph of the parabola if (a) x0 = ¼, (b) x0 = ½, and (c) x0 = 1? (d)
> Find equations of both tangent lines to the graph of the ellipse x2/4 + y2/4 = 1 that pass through the point (4, 0) not on the graph.
> Find all points on the circle x2 + y2 = 100 where the slope is 3/4.
> Find the derivative of the function.
> What is the difference between the (Simple) Power Rule and the General Power Rule?
> Let L be any tangent line to the curve Show that the sum of the x- and y- intercepts of L is c.
> Consider the equation x4 = 4(4x2 – y2) Use a graphing utility to graph the equation. Find and graph the four tangent lines to the curve for y = 3 Find the exact coordinates of the point of intersection of the two tangent lines in the first quadrant.
> Use the graph to answer the questions. Which is greater, the slope of the tangent line at x = -3 3 or the slope of the tangent line at x = -1? Estimate the point(s) where the graph has a vertical tangent line. Estimate the point(s) where the graph has
> The figure below shows the topographic map carried by a group of hikers. The hikers are in a wooded area on top of the hill shown on the map, and they decide to follow the path of steepest descent (orthogonal trajectories to the contours on the map). Dra
> Verify that the two families of curves are orthogonal, where C and K are real numbers. Use a graphing utility to graph the two families for two values of C and two values of K. x2 + y2 = C2 y = Kx
> xy = C, x2 – y2 = k Verify that the two families of curves are orthogonal, where C and K are real numbers. Use a graphing utility to graph the two families for two values of C and two values of K.
> x3 = 3(y - 1) x(3y - 29) = 3 Use a graphing utility to sketch the intersecting graphs of the equations and show that they are orthogonal. [Two graphs are orthogonal if at their point(s) of intersection, their tangent lines are perpendicular to each othe
> Use a graphing utility to sketch the intersecting graphs of the equations and show that they are orthogonal. [Two graphs are orthogonal if at their point(s) of intersection, their tangent lines are perpendicular to each other.] x + y = 0 x = sin y
> Use a graphing utility to sketch the intersecting graphs of the equations and show that they are orthogonal. [Two graphs are orthogonal if at their point(s) of intersection, their tangent lines are perpendicular to each other.] y2 = x3 2x2 + 3y2 = 5
> Find the derivative of the function.
> Use a graphing utility to sketch the intersecting graphs of the equations and show that they are orthogonal. [Two graphs are orthogonal if at their point(s) of intersection, their tangent lines are perpendicular to each other.] 2x2 + y2 = 6 y2 = 4x
> 4x2 + y2 – 8x + 4y + 4 = 0 Find the points at which the graph of the equation has a vertical or horizontal tangent line.
> 25x2 + 16y2 + 200x – 160y + 400 = 0 Find the points at which the graph of the equation has a vertical or horizontal tangent line.
> Two circles of radius 4 are tangent to the graph of y2 = 4x at the point (1, 2). Find equations of these two circles.
> Show that the normal line at any point on the circle x2 + y2 = r2 passes through the origin.
> Find equations for the tangent line and normal line to the circle at each given point. (The normal line at a point is perpendicular to the tangent line at the point.) Use a graphing utility to graph the circle, the tangent lines, and the normal lines. x2
> x2 + y2 = 25 (4, 3), (-3, 4) Find equations for the tangent line and normal line to the circle at each given point. (The normal line at a point is perpendicular to the tangent line at the point.) Use a graphing utility to graph the circle, the tangent l
> Use a graphing utility to graph the equation. Find an equation of the tangent line to the graph at the given point and graph the tangent line in the same viewing window.
> Use a graphing utility to graph the equation. Find an equation of the tangent line to the graph at the given point and graph the tangent line in the same viewing window.
> 3xy − 4 cos x = −6 Find d2y/dx2 implicitly in terms of x and y.
> Find the derivative of the function.
> 7xy + sin x - 2 Find d2y/dx2 implicitly in terms of x and y.
> xy – 1 = 2x + y2 Find d2y/dx2 implicitly in terms of x and y.
> x2y – 2 = 5x + y Find d2y/dx2 implicitly in terms of x and y.
> x2y – 4x = 5 Find d2y/dx2 implicitly in terms of x and y.
> x2 + y2 = 4 Find d2y/dx2 implicitly in terms of x and y.
> Find dy/dx implicitly and find the largest interval of the form –a < y < a or 0 < y < a such that y is a differentiable function of x. Write dy/dx as a function of x. cos y = x
> Find dy/dx implicitly and find the largest interval of the form –a < y < a or 0 < y < a such that y is a differentiable function of x. Write dy/dx as a function of x. tan y = x
> Use implicit differentiation to find an equation of the Show that the equation of the tangent line to the ellipse
> Use implicit differentiation to find an equation of the Show that the equation of the tangent line to the ellipse
> Explain why the derivative of x2 + y2 + 2 = 1 does not mean anything.
> Find the derivative of the function.
> Write two different equations in implicit form that you can write in explicit form. Then write two different equations in implicit form that you cannot write in explicit form.
> Find an equation of the tangent line to the graph at the given point. Kappa curve
> Find an equation of the tangent line to the graph at the given point. Lemniscate
> Find an equation of the tangent line to the graph at the given point. Astroid
> Find an equation of the tangent line to the graph at the given point. Cruciform
> Find an equation of the tangent line to the graph at the given point. Circle
> Find an equation of the tangent line to the graph at the given point. Parabola
> Folium of Descartes: x3 + y3 - 6xy = 0 Find the slope of the tangent line to the graph at the given point.
> Find the slope of the tangent line to the graph at the given point. Bifolium: (x2 + y2)2 = 4x2y
> Find the slope of the tangent line to the graph at the given point. Cissoid: (4 - x)y2 = x3
> Find the derivative of the function.
> Find the slope of the tangent line to the graph at the given point. Witch of Agnesi: (x2 + 4)y = 8
> x cos y = 1, (2, π/3) Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> tan(x + y) = x, (0, 0) Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> x3 + y3 – 6xy – 1, (2, 3) Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> (x + y)3 = x3 + y3, (-1, 1) Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.
> 3x3y = 6, (1, 2) Find dy/dx by implicit differentiation. Then find the slope of the graph at the given point.

