[SOLVED] Rainbows are created when raindrops scatter

Rainbows are created when raindrops scatter sunlight. They have fascinated mankind since ancient times and have inspired attempts at scientific explanation since the time of Aristotle. In this project we use the ideas of Descartes and Newton to explain the shape, location, and colors of rainbows.

//

Transcribed Image Text:

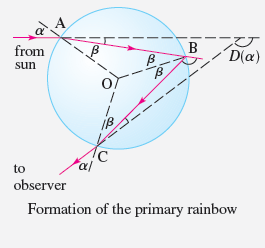
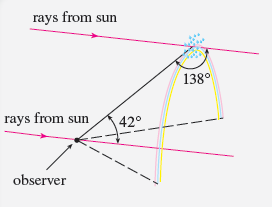
1. The figure shows a ray of sunlight entering a spherical raindrop at A. Some of the light is reflected, but the line AB shows the path of the part that enters the drop. Notice that the light is refracted toward the normal line AO and in fact Snell's Law says that sin a = k sin ß, where a is the angle of incidence, ß is the angle of refraction, and k = is the index of refraction for water. At B some of the light passes through the drop and is refracted into the air, but the line BC shows the part that is reflected. (The angle of inci- dence equals the angle of reflection.) When the ray reaches C, part of it is reflected, but for the time being we are more interested in the part that leaves the raindrop at C. (Notice that it is refracted away from the normal line.) The angle of deviation D(a) is the amount of clockwise rotation that the ray has undergone during this three-stage process. Thus D(a) = (a – B) + ( – 2B) + (a – B) = + 2a – 4B Show that the minimum value of the deviation is D(a) = 138° and occurs when a = 59.4°. A from B B D(a) sun -- -- - to observer Formation of the primary rainbow The significance of the minimum deviation is that when a = 59.4° we have D'(a) - 0, so AD/Aa - 0. This means that many rays with a 59.4° become deviated by approxi- mately the same amount. It is the concentration of rays coming from near the direction of minimum deviation that creates the brightness of the primary rainbow. The figure at the left shows that the angle of elevation from the observer up to the highest point on the rainbow is 180° – 138° = 42°. (This angle is called the rainbow angle.) 2. Problem 1 explains the location of the primary rainbow, but how do we explain the colors? Sunlight comprises a range of wavelengths, from the red range through orange, yellow, green, blue, indigo, and violet. As Newton discovered in his prism experiments of 1666, the index of refraction is different for each color. (The effect is called dispersion.) For red light the refractive index is k - 1.3318, whereas for violet light it is k = 1.3435. By repeating the calculation of Problem 1 for these values of k, show that the rainbow angle is about 42.3° for the red bow and 40.6° for the violet bow. So the rainbow really consists of seven individual bows corresponding to the seven colors. 3. Perhaps you have seen a fainter secondary rainbow above the primary bow. That results from the part of a ray that enters a raindrop and is refracted at A, reflected twice (at B and C), and refracted as it leaves the drop at D (see the figure at the left). This time the devia- tion angle D(a) is the total amount of counterclockwise rotation that the ray undergoes in this four-stage process. Show that rays from sun 138° rays from sun 42° observer 3. Perhaps you have seen a fainter secondary rainbow above the primary bow. That results from the part of a ray that enters a raindrop and is refracted at A, reflected twice (at B and C), and refracted as it leaves the drop at D (see the figure at the left). This time the devia- tion angle D(a) is the total amount of counterclockwise rotation that the ray undergoes in this four-stage process. Show that D(a) = 2a – 6B + 2 and D(a) has a minimum value when k² – 1 cos a = 8 Taking k =, show that the minimum deviation is about 129° and so the rainbow angle for the secondary rainbow is about 51°, as shown in the figure at the left. 4. Show that the colors in the secondary rainbow appear in the opposite order from those in the primary rainbow. © Pichugin Dmitry/Shutterstock.com

Question: Rainbows are created when raindrops scatter

Transcribed Image Text: