Question: Refer to the graph in Fig. 3.
Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property.
Figure 3:
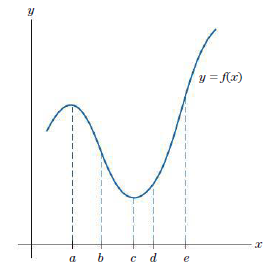
f ’(x) is positive.
Transcribed Image Text:
y a b c d e y = f(x)
> For what x does the function f (x) = 1/4 x2 - x + 2, 0 ≤ x ≤ 8, have its maximum value?
> Let f (x) be the number of people living within x miles of the center of New York City. (a) What does f (10 + h) - f (10) represent? (b) Explain why f ‘(10) cannot be negative.
> The water level in a reservoir varies during the year. Let h(t) be the depth (in feet) of the water at time t days, where t = 0 at the beginning of the year. Match each set of information about h(t) and its derivatives with the corresponding description
> A car is traveling on a straight road and s(t) is the distance traveled after t hours. Match each set of information about s(t) and its derivatives with the corresponding description of the car’s motion. Information A. s(t) is a constant function. B. s’(
> Let f (x) be a function whose derivative is f ‘(x) = √(5x2 + 1). Show that the graph of f (x) has an inflection point at x = 0.
> Let f (x) be a function whose derivative is f ‘(x) = 1/(1 + x2). Note that f ‘(x) is always positive. Show that the graph of f (x) has an inflection point at x = 0.
> Show that the function f (x) = (2x2 + 3) 3/2 is decreasing for x < 0 and increasing for x > 0.
> Let f (x) = (x2 + 2)3/2. Show that the graph of f (x) has a possible relative extreme point at x = 0.
> The tangent line to the curve y = 1/3 x3 - 4x2 + 18x + 22 is parallel to the line 6x - 2y = 1 at two points on the curve. Find the two points.
> Sketch the following curves. y = 1/2x + 2x + 1 (x > 0)
> Sketch the following curves. y = x/5 + 20/x + 3 (x > 0)
> Sketch the following curves. y = x4 - 4x3
> Sketch the following curves. y = x4 - 2x2
> Sketch the following curves. y = x3 - 6x2 - 15x + 50
> Sketch the following curves. y = - 1/3 x3 - 2x2 - 5x
> Sketch the following curves. y = x3 - 3x2 - 9x + 7
> Sketch the following curves. y = 11/3 + 3x - x2 – 1/3 x3
> Sketch the following curves. y = 100 + 36x - 6x2 - x3
> Sketch the following curves. y = x3 - 3x2 + 3x - 2
> If h(x) = [f (x)]2 + 1/g(x), determine h(1) and h’(1), given that f (1) = 1, g(1) = 4, f ‘(1) = -1, and g’(1) = 4.
> Sketch the following curves. y = x3 – 3/2 x2 - 6x
> Sketch the following curves. y = 2x3 + 3x2 + 1
> Sketch the following parabolas. Include their x- and y-intercepts. y = 2x2 + x - 1
> Sketch the following parabolas. Include their x- and y-intercepts. y = -x2 + 20x - 90
> Sketch the following parabolas. Include their x- and y-intercepts. y = -x2 + 8x - 13
> Sketch the following parabolas. Include their x- and y-intercepts. y = x2 + 3x + 2
> Sketch the following parabolas. Include their x- and y-intercepts. y = x2 - 9x + 19
> Sketch the following parabolas. Include their x- and y-intercepts. y = -2x2 + 10x - 10
> Sketch the following parabolas. Include their x- and y-intercepts. y = 4 + 3x - x2
> Sketch the following parabolas. Include their x- and y-intercepts. y = x2 + 3x - 10
> If g(1) = 4 and g’(1) = 3, find f (1) and f ‘(1), where f (x) = 5 * √g(x).
> Sketch the following parabolas. Include their x- and y-intercepts. y = 7 + 6x - x2
> Sketch the following parabolas. Include their x- and y-intercepts. y = 3 - x2
> United States electrical energy production (in trillions of kilowatt-hours) in year t (with 1900 corresponding to t = 0) is given by f (t), where f and its derivatives are graphed in Figs. 5(a) and 5(b). (a) How much electrical energy was produced in 195
> In Figs. 4(a) and 4(b), the t-axis represents time in hours. (a) When is f (t) = 1? (b) Find f (5). (c) When is f (t) changing at the rate of -.08 unit per hour? (d) How fast is f (t) changing after 8 hours? Figure 4: 2.4 2.0 1.6 1.2 .8 4 fi 4 y =
> Property of functions is described next. Draw some conclusion about the graph of the function. H(0) = 0, H’(0) = 0, H’’(0) = 1
> Property of functions is described next. Draw some conclusion about the graph of the function. g(5) = -1, g’(5) = -2, g’’(5) = 0
> Property of functions is described next. Draw some conclusion about the graph of the function. f (4) = -2, f ‘(4) > 0, f ’’(4) = -1
> Property of functions is described next. Draw some conclusion about the graph of the function. G (10) = 2, G’(10) = 0, G’’(10) > 0
> Property of functions is described next. Draw some conclusion about the graph of the function. F ‘(2) = -1, F ’’(2) 6 0
> Property of functions is described next. Draw some conclusion about the graph of the function. h’(3) = 4, h’’(3) = 1
> If g(3) = 2 and g’(3) = 4, find f (3) and f ‘(3), where f (x) = 2 * [g(x)]3.
> Property of functions is described next. Draw some conclusion about the graph of the function. g(1) = 5, g’(1) = -1
> Property of functions is described next. Draw some conclusion about the graph of the function. f (1) = 2, f ‘(1) > 0
> Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property. Figure 3: f ’ (x) is minimized. y a b c d e y = f(x)
> Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property. Figure 3: f ’ (x) is maximized. y a b c d e y = f(x)
> Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property. Figure 3: f ’’(x) is negative. y a b c d e y = f(x)
> Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property. Figure 3: f ’’ (x) is positive. y a b c d e y = f(x)
> Refer to the graph in Fig. 3. List the labeled values of x at which the derivative has the stated property. Figure 3: f ’(x) is negative. y a b c d e y = f(x)
> Draw the graph of a function f (x) for which the function and its first derivative have the stated property for all x. f (x) decreasing and f (x) increasing
> What is the difference between an x-intercept and a zero of a function?
> If f (5) = 2, f ‘(5) = 3, g(5) = 4, and g’(5) = 1, find h(5) and h’(5), where h(x) = 3f (x) + 2g(x).
> What does it mean to say that the graph of f (x) has an inflection point at x = 2?
> Give three characterizations of what it means for the graph of f (x) to be concave up at x = 2. Concave down.
> What is the difference between having a relative maximum at x = 2 and having an absolute maximum at x = 2?
> State as many terms used to describe graphs of functions as you can recall.
> How are the cost, revenue, and profit functions related?
> Outline the procedure for solving an optimization problem.
> What is a constraint equation?
> What is an objective equation?
> Outline a procedure for sketching the graph of a function.
> Outline a method for locating the inflection points of a function.
> Draw the graph of f (x) = 2x + 18/x - 10 in the window [0, 16] by [0, 16]. In what ways is this graph like the graph of a parabola that opens upward? In what ways is it different?
> Outline a method for locating the relative extreme points of a function.
> Give two connections between the graphs of f (x) and f (x).
> State the first-derivative rule. The second-derivative rule.
> What is an asymptote? Give an example.
> How do you determine the y-intercept of a function?
> A one-product firm estimates that its daily total cost function (in suitable units) is C(x) = x3 - 6x2 + 13x + 15 and its total revenue function is R(x) = 28x. Find the value of x that maximizes the daily profit.
> The revenue function for a particular product is R(x) = x (4 - .0001x). Find the largest possible revenue.
> The revenue function for a one-product firm is R(x) = 200 – 1600/(x + 8) - x. Find the value of x that results in maximum revenue.
> If a total cost function is C(x) = .0001x3 - .06x2 + 12x + 100, is the marginal cost increasing, decreasing, or not changing at x = 100? Find the minimum marginal cost.
> Given the cost function C(x) = x3 - 6x2 + 13x + 15, find the minimum marginal cost.
> Figure 3 contains the curves y = f (x), y = g(x), and y = h(x) and the tangent lines to y = f (x) and y = g(x) at x = 1, with h(x) = f (x) + g(x). Find h(1) and h’(1). Figure 3: Y y = y = y = h(x) y = f(x) - 4x + 2.6 26x + 1.1 Fig
> Differentiate. y = x/2 – 2/x
> The cost function for a manufacturer is C(x) dollars, where x is the number of units of goods produced and C, C , and C are the functions given in Fig. 15. Figure 15: (a) What is the cost of manufacturing 60 units of goods? (b) What is the marginal c
> The revenue for a manufacturer is R(x) thousand dollars, where x is the number of units of goods produced (and sold) and R and R are the functions given in Figs. 14(a) and 14(b). Figure 14: Y 80 70 60 50 40 30 20 10 Y 3.2 2.4 1.6 .8 -.8 -1.6 -2.4 -
> Let P(x) be the annual profit for a certain product, where x is the amount of money spent on advertising. (See Fig. 13.) (a) Interpret P(0) (b) Describe how the marginal profit changes as the amount of money spent on advertising increases. (c) Explain th
> A savings and loan association estimates that the amount of money on deposit will be 1 million times the percentage rate of interest. For instance, a 4% interest rate will generate $4 million in deposits. If the savings and loan association can loan all
> The demand equation for a company is p = 200 - 3x, and the cost function is C(x) = 75 + 80x - x2, 0 ≤ x ≤ 40. (a) Determine the value of x and the corresponding price that maximize the profit. (b) If the government imposes a tax on the company of $4 per
> The monthly demand equation for an electric utility company is estimated to be p = 60 - (10-5)x, where p is measured in dollars and x is measured in thousands of kilowatt-hours. The utility has fixed costs of 7 million dollars per month and variable co
> A certain toll road averages 36,000 cars per day when charging $1 per car. A survey concludes that increasing the toll will result in 300 fewer cars for each cent of increase. What toll should be charged to maximize the revenue?
> In the planning of a sidewalk café, it is estimated that for 12 tables, the daily profit will be $10 per table. Because of overcrowding, for each additional table the profit per table (for every table in the café) will be reduced by $.50. How many tables
> A swimming club offers memberships at the rate of $200, provided that a minimum of 100 people join. For each member in excess of 100, the membership fee will be reduced $1 per person (for each member). At most, 160 memberships will be sold. How many memb
> An artist is planning to sell signed prints of her latest work. If 50 prints are offered for sale, she can charge $400 each. However, if she makes more than 50 prints, she must lower the price of all the prints by $5 for each print in excess of the 50. H
> Draw the graph of f (x) = 1/6 x3 – 5/2 x2 + 13x - 20 in the window [0, 10] by [-20, 30]. Algebraically determine the coordinates of the inflection point. Zoom in and zoom out to convince yourself that there are no relative extreme points anywhere.
> The average ticket price for a concert at the opera house was $50. The average attendance was 4000. When the ticket price was raised to $52, attendance declined to an average of 3800 persons per performance. What should the ticket price be to maximize th
> Until recently hamburgers at the city sports arena cost $4 each. The food concessionaire sold an average of 10,000 hamburgers on a game night. When the price was raised to $4.40, hamburger sales dropped off to an average of 8000 per night. (a) Assuming a
> Consider a rectangle in the xy-plane, with corners at (0, 0), (a, 0), (0, b), and (a, b). If (a, b) lies on the graph of the equation y = 30 - x, find a and b such that the area of the rectangle is maximized. What economic interpretations can be given to
> Some years ago, it was estimated that the demand for steel approximately satisfied the equation p = 256 - 50x, and the total cost of producing x units of steel was C(x) = 182 + 56x. (The quantity x was measured in millions of tons and the price and total
> The demand equation for a product is p = 2 - .001x. Find the value of x and the corresponding price, p, that maximize the revenue.
> The demand equation for a certain commodity is p = 1/12 x2 - 10x + 300, 0 ≤ x ≤ 60. Find the value of x and the corresponding price p that maximize the revenue.
> A small tie shop sells ties for $3.50 each. The daily cost function is estimated to be C(x) dollars, where x is the number of ties sold on a typical day and C(x) = .0006x3 - .03x2 + 2x + 20. Find the value of x that will maximize the store’s daily profit
> A furniture store expects to sell 640 sofas at a steady rate next year. The manager of the store plans to order these sofas from the manufacturer by placing several orders of the same size spaced equally throughout the year. The ordering cost for each de
> A pharmacist wants to establish an optimal inventory policy for a new antibiotic that requires refrigeration in storage. The pharmacist expects to sell 800 packages of this antibiotic at a steady rate during the next year. She plans to place several orde
> Refer to Fig. 6. Suppose that (i) the ordering cost for each delivery of dried cherries is $50, and (ii) it costs $7 to carry 1 pound of dried cherries in inventory for 1 year. (a) What is the inventory cost (carrying cost plus ordering cost) if carrying
> Figure 2 contains the curves y = f (x) and y = g(x) and the tangent line to y = f (x) at x = 1, with g(x) = 3 # f (x). Find g(1) and g’(1). Figure 2: y y = .6x + 1 y = f(x) y = g(x) 1 Figure 2 Graphs of f(x) and g(x) = 3f(x). X
> Figure 6 shows the inventory levels of dried Rainier cherries at a natural food store in Seattle and the order–reorder periods over 1 year. Refer to the figure to answer the following questions. (a) What is the average amount of cherrie
> Coffee consumption in the United States is greater on a per capita basis than anywhere else in the world. However, due to price fluctuations of coffee beans and worries over the health effects of caffeine, coffee consumption has varied considerably over
> A pizza box is formed from a 20-cm by 40-cm rectangular piece of cardboard by cutting out six squares of equal size, three from each long side of the rectangle, and then folding the cardboard in the obvious manner to create a box. See Fig. 11. Let x be t

