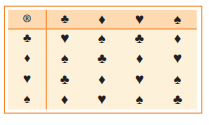
Question: Repeat parts (a)–(h) of Exercise 53
Repeat parts (a)–(h) of Exercise 53 for the mathematical system defined by the given table. Assume that the associative property holds for the given operation.
> 1 ÷ 2 ( ? (mod 5)
> If necessary round all dollar figures to the nearest cent and round percents to the nearest hundredth of a percent. A Pawn Loan Jeffrey wants to take his mother out for dinner on her birthday, so he pawns his watch. The pawnbroker loans Jeffrey $75. Four
> 3 ÷ 4 ( ? (mod 7)
> x + 2y > 4 Draw the graph of the inequality.
> Bank Discount Note Kwame borrowed $2500 for 5 months from a bank using a 3% discount note. (a) How much interest did Kwame pay the bank for the use of its money? (b) How much did he receive from the bank? (c) What was the actual rate of interest he paid?
> Construct a modulo 7 multiplication table. Repeat parts (b)–(g) in Exercise 67.
> Personal Note Aidan runs a car repair garage and needs $6000 to install a new car lift. He borrows the money on a 30-month personal bank note with his mother cosigning the loan. The simple interest rate charged is 5.75%. (a) How much interest does Aidan
> Construct a modulo 8 addition table. Repeat parts (b)–(h) in Exercise 65.
> Business Loan The city of Bradenton is offering simple interest loans to start-up businesses at a rate of 3.5%. Mr. Cannata obtains one of these loans of $6000 for 3 years to help pay for start-up costs of his restaurant, Ortygia. Determine the amount of
> Nursing Shifts A nurse’s work pattern at Community Hospital consists of working the 7 a.m. –3 p.m. shift for 3 weeks and then the 3 p.m. –11 p.m. shift for 2 weeks. a) If it is the third week of the pattern, what shift will the nurse be working 6 weeks f
> p = $1650.00, r = ?, t = 6.5 years, i = $343.20 Use the simple interest formula to determine the missing value. If necessary, round all dollar figures to the nearest cent.
> Physical Therapy A man has an Achilles’ tendon injury and is receiving physical therapy. He must have physical therapy twice a day for 5 days, physical therapy once a day for 3 days, and then 2 days off; then the cycle begins again. If he is in his secon
> p = +800.00, r = 4%, t = ?, i = $64.00 Use the simple interest formula to determine the missing value. If necessary, round all dollar figures to the nearest cent.
> Flight Schedules A pilot is scheduled to fly for 5 consecutive days and rest for 3 consecutive days. If today is the second day of her rest shift, determine whether she will be flying or resting a) 60 days from today. b) 90 days from today. c) 240 days
> Graph the solution set of the inequality, where x is a real number, on the number line.
> (2). To change a fraction to a percent, first divide the numerator by the denominator to obtain a decimal number. Then multiply the decimal number by 100 and add a(n) _______ sign. (4). To change a percent to a decimal number, divide the number by 100 an
> p = ?, r = 2.1%, t = 135 days, i = $37.80 Use the simple interest formula to determine the missing value. If necessary, round all dollar figures to the nearest cent.
> Governors’ Elections Wisconsin gubernatorial elections (elections for governor) have been held every four years starting in 1970. Each of these years is congruent to 2 in modulo 4. a) List the first five Wisconsin gubernatorial election years held after
> p =$41,864, r = 0.0375% per day, t = 60 days Determine the simple interest. Unless noted otherwise, assume the rate is an annual rate. Assume 360 days in a year. Round answers to the nearest cent.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. ? - 3 = 4 (mod 8)
> Determine the simple interest. Unless noted otherwise, assume the rate is an annual rate. Assume 360 days in a year. Round answers to the nearest cent. p = $550.31, r = 8.9%, t = 67 days
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. 3 • ? = 3 (mod 12)
> Determine the simple interest. Unless noted otherwise, assume the rate is an annual rate. Assume 360 days in a year. Round answers to the nearest cent.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. 3 • ? = 5 (mod 6)
> p = $6742.75, r = 6.05%, t = 90 days Determine the simple interest. Unless noted otherwise, assume the rate is an annual rate. Assume 360 days in a year. Round answers to the nearest cent.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. 4 • ? = 3 (mod 7)
> y = x + 3 y = -1 Solve the system of equations graphically. If the system does not have a single ordered pair as a solution, state whether the system is inconsistent or dependent.
> The identity element is C. Determine the inverse, if it exists, of (a) A, (b) B, and (c) C.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. 3 - ? = 7 (mod 9)
> Determine if the system has an identity element. If so, list the identity element. Explain how you determined your answer.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. 4 + ? = 3 (mod 6)
> Determine if the system is closed. Explain how you determined your answer.
> Determine all positive number replacements (less than the modulus) for the question mark that make the statement true. ? + 3 = 2 (mod 5)
> In Exercises 67 and 68 the tables shown below and on the next page are examples of noncommutative, or nonabelian, groups. For each exercise, do the following.
> Find the modulo class to which each number belongs for the indicated modulo system. -39, mod 7
> (a) Let E and O represent even numbers and odd numbers, respectively, as in Exercise 65. Complete the table for the operation of multiplication. (b) Determine whether this mathematical system forms a commutative group under the operation of multiplicatio
> Find the modulo class to which each number belongs for the indicated modulo system. -7, mod 4
> The time it takes an ice cube to melt in water and the temperature of the water Use your intuition to determine whether the variation between the indicated quantities is direct or inverse.
> For the mathematical system given, determine which of the five properties of a commutative group do not hold.
> Find the modulo class to which each number belongs for the indicated modulo system. 75, mod 8
> For the mathematical system given, determine which of the five properties of a commutative group do not hold.
> Find the modulo class to which each number belongs for the indicated modulo system. 43, mod 6
> For the mathematical system given, determine which of the five properties of a commutative group do not hold.
> Find the modulo class to which each number belongs for the indicated modulo system. 38, mod 9
> Consider the mathematical system defined by the following table. (a) Is the system closed? Explain. (b) Is there an identity element in the set? If so, what is it? c) For each element in the set, give the corresponding inverse element, if it exists. (d)
> Determine what number the sum, difference, or product is congruent to in modulo 5. (4 – 9) • 7
> Repeat parts (a)–(h) of Exercise 53 for the mathematical system defined by the given table. Assume that the associative property holds for the given operation.
> Determine what number the sum, difference, or product is congruent to in modulo 5. 2 - 4
> Determine (a) the area and (b) the circumference of the circle. Use the key on your calculator and round your answer to the nearest hundredth.
> Determine what number the sum, difference, or product is congruent to in modulo 5. 8 . 7
> A mathematical system is defined by a three-element by three-element table where every element in the set appears in each row and each column. Must the mathematical system be a commutative group? Explain.
> Determine what number the sum, difference, or product is congruent to in modulo 5. 12 - 5
> Determine the sum or difference in clock 7 arithmetic. 3 – (2 – 6)
> Determine what number the sum, difference, or product is congruent to in modulo 5. 2 + 3
> Determine the sum or difference in clock 7 arithmetic. 2 – 3
> Consider the 12 months to be a modulo 12 system with January being month 0. If it is currently October, determine the month it will be in the specified number of months. 5 years, 9 months
> Determine the sum or difference in clock 7 arithmetic. 6 + 7
> Consider the 12 months to be a modulo 12 system with January being month 0. If it is currently October, determine the month it will be in the specified number of months. 7 years
> y < -2x + 2 Draw the graph of the inequality.
> Determine the sum or difference in clock 7 arithmetic. 2 + 6
> Consider the 12 months to be a modulo 12 system with January being month 0. If it is currently October, determine the month it will be in the specified number of months. 4 years, 8 months
> Determine the sum or difference in clock 6 arithmetic. 2 + (1 – 3)
> Assume that Sunday is represented as day 0, Monday is represented as day 1, and so on. If today is Thursday (day 4), determine the day of the week it will be in the specified number of days. Assume no leap years. 3 years, 25 days
> Determine the sum or difference in clock 6 arithmetic. 4 – 5
> Assume that Sunday is represented as day 0, Monday is represented as day 1, and so on. If today is Thursday (day 4), determine the day of the week it will be in the specified number of days. Assume no leap years. 3 years, 34 days
> Determine the sum or difference in clock 6 arithmetic. 4 + 6
> Assume that Sunday is represented as day 0, Monday is represented as day 1, and so on. If today is Thursday (day 4), determine the day of the week it will be in the specified number of days. Assume no leap years. 365 days
> Determine the sum or difference in clock 6 arithmetic. 4 + 4
> Give an example to show that the associative property does not hold for the set of integers under the operation of subtraction.
> Graph the solution set of the inequality, where x is a real number, on the number line.
> Determine the difference in clock 12 arithmetic by starting at the first number and counting counterclockwise on the clock the number of units given by the second number. 12 – 12
> Give an example to show that the commutative property does not hold for the set of integers under the operation of division.
> Determine the difference in clock 12 arithmetic by starting at the first number and counting counterclockwise on the clock the number of units given by the second number. 5 – 8
> Give the associative property of addition and illustrate the property with an example.
> Determine the difference in clock 12 arithmetic by starting at the first number and counting counterclockwise on the clock the number of units given by the second number. 1 – 12
> Give the commutative property of multiplication and illustrate the property with an example.
> Determine the difference in clock 12 arithmetic by starting at the first number and counting counterclockwise on the clock the number of units given by the second number. 11 – 8
> Is the set of irrational numbers a group under the operation of multiplication
> Use Table 9.1 on page 529 to determine the sum in clock 12 arithmetic. 18 + 72 + 6
> Is the set of rational numbers a group under the operation of subtraction?
> Solve the system of equations graphically. If the system does not have a single ordered pair as a solution, state whether the system is inconsistent or dependent. y = 3 y = x - 1
> Use Table 9.1 on page 529 to determine the sum in clock 12 arithmetic. 12 + 12
> Is the set of integers a group under the operation of multiplication
> Use Table 9.1 on page 529 to determine the sum in clock 12 arithmetic. 11 + 7
> Is the set of whole numbers a commutative group under the operation of multiplication?
> Use Table 9.1 on page 529 to determine the sum in clock 12 arithmetic. 10 + 3
> Is the set of negative integers a group under the operation of division?
> Determine if the system is commutative.Explain how you determined your answer.
> Is the set of positive rational numbers a commutative group under the operation of multiplication?
> Determine (a) the volume and (b) the surface area of the three-dimensional figure. When appropriate, use the key on your calculator and round your answer to the nearest hundredth.
> Is the set of whole numbers a commutative group under the operation of addition?
> Use your intuition to determine whether the variation between the indicated quantities is direct or inverse. On Earth, the weight and mass of an object
> More Pool Toys Wacky Noodle Pool Toys (see Exercise 44 on page 479) come in many different shapes and sizes. (a) Determine the volume, in cubic inches, of a noodle that is in the shape of a 5.5-ft-long solid octagonal prism whose base has an area of 5 in
> Is the set of real numbers a group under the operation of addition?
> If the side of a cube is doubled, how is the volume of the cube affected?
> State the theorem concerning the sum of the measures of the angles of a triangle in a) Euclidean geometry. b) Hyperbolic geometry. c) Elliptical geometry.
> Packing Orange Juice A box is packed with six cans of orange juice. The cans are touching each other and the sides of the box, as shown. What percent of the volume of the interior of the box is not occupied by the cans?
> List the three types of curvature of space and the types of geometry that correspond to them.
> In Exercises 47–52, find the missing value indicated by the question mark. Use the following formula.
> In forming the Koch snowflake in Figure 8.104 on page 510, the perimeter becomes greater at each step in the process. If each side of the original triangle is 1 unit, a general formula for the perimeter, L, of the snowflake at any step, n, may be found b

