Question: Repeat Prob. 11–49 for a water
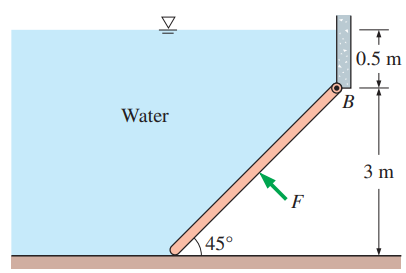
Repeat Prob. 11–49 for a water height of 0.8 m above the hinge at B.
Data from Prob. 11-49:
The 280-kg, 6-m-wide rectangular gate shown in Fig. P11–49 is hinged at B and leans against the floor at A, making an angle of 45° with the horizontal. The gate is to be opened from its lower edge by applying a normal force at its center. Determine the minimum force F required to open the water gate.
> A person is filling a knee-high bucket with water using a garden hose and holding it such that water discharges from the hose at the level of his waist. Someone suggests that the bucket will fill faster if the hose is lowered such that water discharges f
> A 3-m-high tank filled with water has a discharge valve near the bottom and another near the top. (a) If these two valves are opened, will there be any difference between the discharge velocities of the two water streams? (b) If a hose whose discharge en
> The water level in a tank is 20 m above the ground. A hose is connected to the bottom of the tank, and the nozzle at the end of the hose is pointed straight up. The water stream from the nozzle is observed to rise 25 m above the ground. Explain what may
> What is the kinetic energy correction factor? Is it significant?
> At a certain location, wind is blowing steadily at 10 m/s. Determine the mechanical energy of air per unit mass and the power generation potential of a wind turbine with 60-m-diameter blades at that location. Take the air density to be 1.25 kg/m3.
> Consider the steady adiabatic flow of an incompressible fluid. If the temperature of the fluid remains constant during flow, is it accurate to say that the frictional effects are negligible?
> What is streamwise acceleration? How does it differ from normal acceleration? Can a fluid particle accelerate in steady flow?
> Consider the steady adiabatic flow of an incompressible fluid. Can the temperature of the fluid decrease during flow? Explain.
> What is useful pump head? How is it related to the power input to the pump?
> What is irreversible head loss? How is it related to the mechanical energy loss?
> Water enters a tank of diameter DT steadily at a mass flow rate of min.in. An orifice at the bottom with diameter Do allows water to escape. The orifice has a rounded entrance, so the frictional losses are negligible. If the tank is initially empty, (a)
> In cold climates, water pipes may freeze and burst if proper precautions are not taken. In such an occurrence, the exposed part of a pipe on the ground ruptures, and water shoots up to 55 m. Estimate the gage pressure of water in the pipe. State your ass
> The air velocity in a duct is measured by a Pitotstatic probe connected to a differential pressure gage. If the air is at 13.4 psia absolute and 70°F and the reading of the differential pressure gage is 0.15 psi, determine the air velocity.
> The water level in a tank is 20 m above the ground. A hose is connected to the bottom of the tank, and the nozzle at the end of the hose is pointed straight up. The tank cover is airtight, and the air pressure above the water surface is 2 atm gage. The s
> Air is flowing through a venturi meter whose diameter is 2.6 in at the entrance part (location 1) and 1.8 in at the throat (location 2). The gage pressure is measured to be 12.2 psia at the entrance and 11.8 psia at the throat. Neglecting frictional eff
> Consider a river flowing toward a lake at an average velocity of 3 m/s at a rate of 500 m3/s at a location 90 m above the lake surface. Determine the total mechanical energy of the river water per unit mass and the power generation potential of the entir
> Reconsider Prob. 12–30. Using appropriate software, investigate the effect of water height in the tank on the discharge velocity. Let the water height vary from 0 to 5 m in increments of 0.5 m. Tabulate and plot the results. Data from
> A pressurized tank of water has a 10-cm-diameter orifice at the bottom, where water discharges to the atmosphere. The water level is 2.5 m above the outlet. The tank air pressure above the water level is 250 kPa (absolute) while the atmospheric pressure
> Define static, dynamic, and hydrostatic pressure. Under what conditions is their sum constant for a flow stream?
> The water pressure in the mains of a city at a particular location is 270 kPa gage. Determine if this main can serve water to neighborhoods that are 25 m above this location.
> Water at 20°C is siphoned from a reservoir as shown in Fig. P12–28. For d = 8 cm and D = 16 cm, determine (a) the minimum flow rate that can be achieved without cavitation occurring in the piping system and (b) the maximum e
> Air at 105 kPa and 37°C flows upward through a 6-cm diameter inclined duct at a rate of 65 L/s. The duct diameter is then reduced to 4 cm through a reducer. The pressure change across the reducer is measured by a water manometer. The elevation
> Reconsider Prob. 12–25. Using appropriate software, investigate the effect of the discharge pipe diameter on the time required to empty the pool completely. Let the diameter vary from 1 to 10 cm in increments of 1 cm. Tabulate and plot the results. Data
> Reconsider Prob. 12–24. Determine how long it will take to empty the swimming pool completely. Data from Prob. 12-24: The water in an 8-m-diameter, 3-m-high above-ground swimming pool is to be emptied by unplugging a 3-cm-diameter, 25-m-long horizontal
> The water in an 8-m-diameter, 3-m-high above-ground swimming pool is to be emptied by unplugging a 3-cm-diameter, 25-m-long horizontal pipe attached to the bottom of the pool. Determine the maximum discharge rate of water through the pipe. Also, explain
> While traveling on a dirt road, the bottom of a car hits a sharp rock and a small hole develops at the bottom of its gas tank. If the height of the gasoline in the tank is 30 cm, determine the initial velocity of the gasoline at the hole. Discuss how the
> A water jet that leaves a nozzle at 60 m/s at a flow rate of 120 kg/s is to be used to generate power by striking the buckets located on the perimeter of a wheel. Determine the power generation potential of this water jet.
> An airplane is flying at an altitude of 10,500 m. Determine the gage pressure at the stagnation point on the nose of the plane if the speed of the plane is 450 km/h. How would you solve this problem if the speed were 1050 km/h? Explain.
> Water flows through a horizontal pipe at a rate of 2.4 gal/s. The pipe consists of two sections of diameters 4 in and 2 in with a smooth reducing section. The pressure difference between the two pipe sections is measured by a mercury manometer. Neglectin
> A siphon pumps water from a large reservoir to a lower tank that is initially empty. The tank also has a rounded orifice 20 ft below the reservoir surface where the water leaves the tank. Both the siphon and the orifice diameters are 2 in. Ignoring frict
> What are the three major assumptions used in the derivation of the Bernoulli equation?
> The diameter of a cylindrical water tank is Do and its height is H. The tank is filled with water, which is open to the atmosphere. An orifice of diameter D with a smooth entrance (i.e., negligible losses) is open at the bottom. Develop a relation for th
> A piezometer and a Pitot tube are tapped into a 4-cm diameter horizontal water pipe, and the heights of the water columns are measured to be 26 cm in the piezometer and 35 cm in the Pitot tube (both measured from the top surface of the pipe). Determine
> The air velocity in the duct of a heating system is to be measured by a Pitot-static probe inserted into the duct parallel to the flow. If the differential height between the water columns connected to the two outlets of the probe is 3.2 cm, determine (a
> A Pitot-static probe is used to measure the speed of an aircraft flying at 3000 m. If the differential pressure reading is 3 kPa, determine the speed of the aircraft.
> In a hydroelectric power plant, water enters the turbine nozzles at 800 kPa absolute with a low velocity. If the nozzle outlets are exposed to atmospheric pressure of 100 kPa, determine the maximum velocity to which water can be accelerated by the nozzl
> A student siphons water over an 8.5-m-high wall at sea level. She then climbs to the summit of Mount Shasta (elevation 4390 m, Patm = 58.5 kPa) and attempts the same experiment. Comment on her prospects for success.
> Determine the specific potential energy, in kJ/kg, of an object 50 m above a datum in a location where g = 9.8 m/s2.
> Explain how and why a siphon works. Someone proposes siphoning cold water over a 7-m-high wall. Is this feasible? Explain.
> The water level of a tank on a building roof is 20 m above the ground. A hose leads from the tank bottom to the ground. The end of the hose has a nozzle, which is pointed straight up. What is the maximum height to which the water could rise? What factors
> The velocity of a fluid flowing in a pipe is to be measured by two different Pitot-type mercury manometers shown in Fig. P12–11C. Would you expect both manometers to predict the same velocity for flowing water? If not, which would be mo
> A glass manometer with oil as the working fluid is connected to an air duct as shown in Fig. P12–10C. Will the oil levels in the manometer be as in Fig. P12–10Ca or b? Explain. What would your response be if the flow d
> Express the Bernoulli equation in three different ways using (a) energies, (b) pressures, and (c) heads.
> A cylindrical tank is fully filled with water (Fig. P11–9). In order to increase the flow from the tank, an additional pressure is applied to the water surface by a compressor. For P0 = 0, P0 = 5 bar, and P0 = 10 bar, calculate the hydr
> Consider a 200-ft-high, 1200-ft-wide dam filled to capacity. Determine (a) the hydrostatic force on the dam and (b) the force per unit area of the dam near the top and near the bottom.
> Consider a circular surface subjected to hydrostatic forces by a constant density liquid. If the magnitudes of the horizontal and vertical components of the resultant hydrostatic force are determined, explain how you would find the line of action of this
> Consider a submerged curved surface. Explain how you would determine the vertical component of the hydrostatic force acting on this surface.
> The volume of a rock is to be determined without using any volume measurement devices. Explain how you would do this with a waterproof spring scale.
> Calculate the total potential energy, in Btu, of an object that is 20 ft below a datum level at a location where g = 31.7 ft/s2 and which has a mass of 100 lbm.
> Consider a submerged curved surface. Explain how you would determine the horizontal component of the hydrostatic force acting on this surface.
> The 280-kg, 6-m-wide rectangular gate shown in Fig. P11–49 is hinged at B and leans against the floor at A, making an angle of 45° with the horizontal. The gate is to be opened from its lower edge by applying a normal force a
> A raft is made using a number of logs 25 cm in diameter and 2 m long, as shown in the figure. It is desired that a maximum 90 percent volume of each log will be submerged when carrying two boys weighing 400 N each. Determine the minimum number of logs th
> The water in a 25-m-deep reservoir is kept inside by a 90-m-wide wall whose cross section is an equilateral triangle, as shown in Fig. P11–47. Determine (a) the total force (hydrostatic + atmospheric) acting on the inner surface of the
> A 30-ton, 4-m-diameter hemispherical dome on a level surface is filled with water, as shown in Fig. P11–46. Someone claims that he can lift this dome by making use of Pascal’s law by attaching a long tube to the top an
> A semicircular 40-ft-diameter tunnel is to be built under a 150-ft-deep, 800-ft-long lake, as shown in Fig. P11–45E. Determine the total hydrostatic force acting on the roof of the tunnel.
> Repeat Prob. 11–43 for a total water height of 2 m. Data from Prob. 11-43: A 3-m-high, 5-m-wide rectangular gate is hinged at the top edge at A and is restrained by a fixed ridge at B. Determine the hydrostatic force exerted on the gat
> A 3-m-high, 5-m-wide rectangular gate is hinged at the top edge at A and is restrained by a fixed ridge at B. Determine the hydrostatic force exerted on the gate by the 5-m-high water and the location of the pressure center.
> Reconsider Prob. 11–41. Using appropriate software, investigate the effect of air pressure above water on the cable force. Let this pressure vary from 0.5 MPa to 15 MPa. Plot the cable force versus the air pressure. Data from Prob. 11-
> Determine the specific kinetic energy of a mass whose velocity is 30 m/s, in kJ/kg.
> What is the weight, in N, of an object with a mass of 200 kg at a location where g = 9.6 m/s2?
> An elastic air balloon having a diameter of 30 cm is attached to the base of a container partially filled with water at +4°C, as shown in Fig. P11–41. If the pressure of the air above the water is gradually increased from 100
> The 0.5-m-radius semicircular gate shown in the figure is hinged through the top edge AB. Find the required force to be applied at the center of gravity to keep the gate closed.
> A submerged horizontal flat plate is suspended in water by a string attached at the centroid of its upper surface. Now the plate is rotated 45° about an axis that passes through its centroid. Discuss the change in the hydrostatic force acting on the top
> An air-conditioning system requires a 34-m-long section of 12-cm-diameter ductwork to be laid underwater. Determine the upward force the water will exert on the duct. Take the densities of air and water to be 1.3 kg/m3 and 1000 kg/m3, respectively.
> The weight of a body is usually measured by disregarding buoyancy force applied by the air. Consider a 20-cm-diameter spherical body of density 7800 kg/m3. What is the percentage error associated with neglecting air buoyancy?
> A cone floats in the glycerin (SG = 1.26), as shown in the figure. Find the mass of the cone.
> One of the common procedures in fitness programs is to determine the fat-to-muscle ratio of the body. This is based on the principle that the muscle tissue is denser than the fat tissue, and, thus, the higher the average density of the body, the higher i
> It is estimated that 90 percent of an iceberg’s volume is below the surface, while only 10 percent is visible above the surface. For seawater with a density of 1025 kg/m3, estimate the density of the iceberg.
> It is said that Archimedes discovered his principle during a bath while thinking about how he could determine if King Hiero’s crown was actually made of pure gold. While in the bathtub, he conceived the idea that he could determine the average density of
> The density of a liquid is to be determined by an old 1-cm-diameter cylindrical hydrometer whose division marks are completely wiped out. The hydrometer is first dropped in water, and the water level is marked. The hydrometer is then dropped into the oth
> The specific kinetic energy of a moving mass is given by ke = V2/2, where V is the velocity of the mass. Determine the specific kinetic energy of a mass whose velocity is 100 ft/s, in Btu/lbm.
> The hull of a boat has a volume of 180 m3, and the total mass of the boat when empty is 8560 kg. Determine how much load this boat can carry without sinking (a) in a lake and (b) in seawater with a specific gravity of 1.03.
> A 200-kg granite rock (ρ = 2700 kg/m3) is dropped into a lake. A man dives in and tries to lift the rock. Determine how much force the man needs to apply to lift it from the bottom of the lake. Do you think he can do it?
> Consider two identical spherical balls submerged in water at different depths. Will the buoyant forces acting on these two balls be the same or different? Explain.
> Someone claims that she can determine the magnitude of the hydrostatic force acting on a plane surface submerged in water regardless of its shape and orientation if she knows the vertical distance of the centroid of the surface from the free surface and
> Consider a 3-kg copper cube and a 3-kg copper ball submerged in a liquid. Will the buoyant forces acting on these two bodies be the same or different? Explain.
> Consider two 5-cm-diameter spherical balls—one made of aluminum, the other of iron—submerged in water. Will the buoyant forces acting on these two balls be the same or different? Explain.
> Discuss the stability of (a) a submerged and (b) a floating body whose center of gravity is above the center of buoyancy.
> What is buoyant force? What causes it? What is the magnitude of the buoyant force acting on a submerged body whose volume is V? What are the direction and the line of action of the buoyant force?
> Repeat Prob. 11–24 for a radius of 2 m for the gate. Data from Prob. 11-24: A 4-m-long quarter-circular gate of radius 3 m and of negligible weight is hinged about its upper edge A, as shown in Fig. P11–24. The gate c
> A 4-m-long quarter-circular gate of radius 3 m and of negligible weight is hinged about its upper edge A, as shown in Fig. P11–24. The gate controls the flow of water over the ledge at B, where the gate is pressed by a spring. Determine
> What is the difference between the macroscopic and microscopic forms of energy?
> Repeat Prob. 11–22 for the case of a partially filled trough with a water height of 0.35 m directly above the hinge. Data from Prob. 11-22: The two sides of a V-shaped water trough are hinged to each other at the bottom where they meet
> The two sides of a V-shaped water trough are hinged to each other at the bottom where they meet, as shown in Fig. P11–22, making an angle of 45° with the ground from both sides. Each side is 0.75 m wide, and the two parts are
> A long, solid cylinder of radius 2 ft hinged at point A is used as an automatic gate, as shown in Fig. P11–21E. When the water level reaches 12 ft, the cylindrical gate opens by turning about the hinge at point A. Determine (a) the hydr
> For a gate width of 2 m into the paper (Fig. P11–20), determine the force required to hold the gate ABC at its location.
> You may have noticed that dams are much thicker at the bottom. Explain why dams are built that way.
> Repeat Prob. 11–18E for a water height of 6 ft. Data from Prob. 11-18: The flow of water from a reservoir is controlled by a 5-ft-wide L-shaped gate hinged at point A, as shown in Fig. P11–18E. If it is desired that t
> The flow of water from a reservoir is controlled by a 5-ft-wide L-shaped gate hinged at point A, as shown in Fig. P11–18E. If it is desired that the gate open when the water height is 12 ft, determine the mass of the required weight W.
> Reconsider Prob. 11–16. Using appropriate software, investigate the effect of water depth on the force exerted on the plate by the ridge. Let the water depth vary from 0 to 5 m in increments of 0.5 m. Tabulate and plot your results. Da
> A 6-m-high, 5-m-wide rectangular plate blocks the end of a 5-m-deep freshwater channel, as shown in Fig. P11–16. The plate is hinged about a horizontal axis along its upper edge through a point A and is restrained from opening by a fixe
> Determine the resultant force acting on the 0.7-m-high and 0.7-m-wide triangular gate shown in Fig. P11–15 and its line of action.
> Is the state of the air in an isolated room completely specified by the temperature and the pressure? Explain.
> A water trough of semicircular cross section of radius 0.6 m consists of two symmetric parts hinged to each other at the bottom, as shown in Fig. P11–14. The two parts are held together by a cable and turnbuckle placed every 3 m along t
> The water side of the wall of a 70-m-long dam is a quarter circle with a radius of 7 m. Determine the hydrostatic force on the dam and its line of action when the dam is filled to the rim.
> A room in the lower level of a cruise ship has a 40-cm-diameter circular window. If the midpoint of the window is 2 m below the water surface, determine the hydrostatic force acting on the window, and the pressure center. Take the specific gravity of sea
> Consider a heavy car submerged in water in a lake with a flat bottom. The driver’s side door of the car is 1.1 m high and 0.9 m wide, and the top edge of the door is 10 m below the water surface. Determine the net force acting on the door (normal to its
> Consider an 8-m-long, 8-m-wide, and 2-m-high above ground swimming pool that is filled with water to the rim. (a) Determine the hydrostatic force on each wall and the distance of the line of action of this force from the ground. (b) If the height of the
> Define the resultant hydrostatic force acting on a submerged surface, and the center of pressure.
> What four processes make up the simple ideal Rankine cycle?

