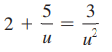Question: Solve Problem by Using any method. /
> perform the indicated operations and simplify.
> The price of gas increased 4% in one week. If the price last week was $4.30 per gallon, what is the price now? (Round to the nearest cent).
> Subtract the sum of the first two polynomials from the sum of the last two: 3m2 - 2m + 5, 4m2 - m, 3m2 - 3m - 2, m3 + m2 + 2
> If you paid $29.86 in tax on a purchase of $533.19, what was the sales tax rate? (Write as a percentage, rounded to one decimal place).
> perform the indicated operations and simplify.
> without using a calculator, round to the nearest integer.
> perform the indicated operations and simplify.
> without using a calculator, round to the nearest integer
> perform the indicated operations and simplify.
> Use a calculator to express each number in Problem as a decimal to the capacity of your calculator. Observe the repeating decimal representation of the rational numbers and the nonrepeating decimal representation of the irrational numbers.
> refer to the following polynomials: Add (A) and (B).
> perform the indicated operations and simplify.
> Repeat Problem 37 for 0.181818 . . . . . Data from Problem 37: Proceeding similarly, convert the repeating decimal 0.090909c into a fraction. (All repeating decimals are rational numbers, and all rational numbers have repeating decimal representations.)
> perform the indicated operations and simplify.
> Indicate true (T) or false (F), and for each false statement find real number replacements for a and b that will provide a counterexample. For all real numbers a and b, (A) a + b = b + a (B) a - b = b - a (C) ab = ba (D) a ÷ b = b ÷ a
> perform the indicated operations and simplify.
> Given the sets of numbers N, Z, Q, and R , indicate to which set(s) each of the following numbers belongs: (A) -3 (B) 3.14 (C) π (D) 2/3
> perform the indicated operations and simplify.
> Give an example of a rational number that is not an integer.
> perform the indicated operations and simplify.
> Indicate whether the following are true (T) or false (F): (A) All natural numbers are integers. (B) All real numbers are irrational. (C) All rational numbers are real numbers.
> Replace each question mark with an appropriate expression that will illustrate the use of the indicated real number property. Associative property ( ∙ ) : x(yz) = ?
> perform the indicated operations and simplify.
> If uv = 0, does either u or v have to be 0? Explain.
> factor completely. If a polynomial cannot be factored, say so.
> perform the indicated operations and simplify.
> factor completely. If a polynomial cannot be factored, say so.
> perform the indicated operations and simplify.
> factor completely. If a polynomial cannot be factored, say so.
> perform the indicated operations and simplify.
> factor completely. If a polynomial cannot be factored, say so.
> Solve Problem by Factoring.
> Solve Problem by Factoring.
> Solve Problem by the square-root method.
> Solve Problem by the square-root method.
> It is of considerable importance to know the least number of feet d in which a car can be stopped, including reaction time of the driver, at various speeds v (in miles per hour). Safety research has produced the formula d = 0.044v2 + 1.1v. If it took a c
> Using the formula in Problem 51, determine the interest rate that will make $1,000 grow to $1,210 in 2 years. Data from Problem 51: If P dollars are invested at 100r percent compounded annually, at the end of 2 years it will grow to A = P(1 + r)2 . At w
> An importer sells an automatic camera to outlets in a large city. During the summer, the weekly supply-and-demand equations are How many units are required for supply to equal demand? At what price will supply equal demand?
> perform the indicated operations and simplify.
> refer to the following polynomials: What is the degree of (A)?
> In Problem , find all real solutions.
> In Problem , find all real solutions.
> In Problem , find all real solutions.
> Consider the quadratic equation x2 - 2x + c = 0 here c is a real number. Discuss the relationship between the values of c and the three types of roots listed in Table 1 on page 910.
> Solve x2 + 3mx - 3n = 0 for x in terms of m and n.
> factor, if possible, as the product of two first degree polynomials with integer coefficients. Use the quadratic formula and the factor theorem.
> factor, if possible, as the product of two first degree polynomials with integer coefficients. Use the quadratic formula and the factor theorem.
> factor, if possible, as the product of two first degree polynomials with integer coefficients. Use the quadratic formula and the factor theorem.
> In problem factor, if possible, as the product of two first degree polynomials with integer coefficients. Use the quadratic formula and the factor theorem.
> factor by grouping.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using any method.
> Solve Problem by Using the quadric formula.
> Solve Problem by Using the quadric formula.
> perform the indicated operations and simplify.
> Change each expression to rational exponent form. Do not simplify.
> Change each expression in Problem to radical form. Do not simplify.
> Change each expression in Problem to radical form. Do not simplify.
> Change each expression in Problem to radical form. Do not simplify. 7y2/5
> evaluate each expression on a calculator and determine which pairs have the same value. Verify these results algebraically.
> evaluate using a calculator. (Refer to the instruction book for your calculator to see how exponential forms are evaluated.) 2.8768/5
> evaluate using a calculator. (Refer to the instruction book for your calculator to see how exponential forms are evaluated.) 103-3/4
> evaluate using a calculator. (Refer to the instruction book for your calculator to see how exponential forms are evaluated.) 155/4
> simplify by writing each expression as a simple or single fraction reduced to lowest terms and without negative exponents
> simplify by writing each expression as a simple or single fraction reduced to lowest terms and without negative exponents
> factor by grouping.
> simplify by writing each expression as a simple or single fraction reduced to lowest terms and without negative exponents
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample.
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample.
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample. If r > 0, then r has three cube roots.
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample. If r < 0, then r has no square roots
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample.
> discuss the validity of each statement. If the statement is true, explain why. If not, give a counterexample.
> Illustrate common errors involving rational exponents. In each case, find numerical examples that show that the left side is not always equal to the right side.
> Illustrate common errors involving rational exponents. In each case, find numerical examples that show that the left side is not always equal to the right side.
> Rationalize the numerators in Problem.
> perform the indicated operations and simplify.
> Rationalize the numerators in Problem.
> Rationalize the numerators in Problem.
> Rationalize the denominators
> Rationalize the denominators
> Rationalize the denominators
> Write each expression in the form axp + bxq , where a and b are real numbers and p and q are rational numbers.
> Write each expression in the form axp + bxq , where a and b are real numbers and p and q are rational numbers.
> Write each expression in the form axp + bxq , where a and b are real numbers and p and q are rational numbers.
> multiply, and express answers using positive exponents only.
> multiply, and express answers using positive exponents only.
> factor by grouping.
> multiply, and express answers using positive exponents only.
> multiply, and express answers using positive exponents only.
> Simplify each expression using properties of radicals. All variables represent positive real numbers.
> Simplify each expression using properties of radicals. All variables represent positive real numbers.
> Simplify each expression using properties of radicals. All variables represent positive real numbers.
> simplify each expression and write answers using positive exponents only. All variables represent positive real numbers.