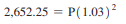Question: Solve the equation for the unknown quantity. (
> pertain to the following input–output model: Assume that an economy is based on three industrial sectors: agriculture (A), building (B), and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. How
> Pertain to the following input–output model: Assume that an economy is based on two industrial sectors, agriculture (A) and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. Repeat Problem 12 for D3. Data from p
> Pertain to the following input–output model: Assume that an economy is based on two industrial sectors, agriculture (A) and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. Find the output for each sector that i
> Pertain to the following input–output model: Assume that an economy is based on two industrial sectors, agriculture (A) and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. How much input from A and E are requi
> Solve each equation for x, where x represents a real number.
> Solve the equation for the unknown quantity. (If necessary, review sections A.7, 2.5, and 2.6.)
> Solve each equation for x, where x represents a real number. Answer:
> Solve each equation for x, where x represents a real number.
> Solve each equation for x, where x represents a real number. Answer:
> Repeat Problem 41 with the following table. Data from problem 41: An economy is based on four sectors, agriculture (A), energy (E), labor (L), and manufacturing (M). The table gives the input requirements for a dollar’s worth of output
> A large energy company produces electricity, natural gas, and oil. The production of a dollar’s worth of electricity requires inputs of $0.30 from electricity, $0.10 from natural gas, and $0.20 from oil. Production of a dollar’s worth of natural gas requ
> The economy of a country is based on two sectors, agriculture and oil. Production of a dollar’s worth of agriculture requires an input of $0.40 from agriculture and $0.35 from oil. Production of a dollar’s worth of oil requires an input of $0.20 from agr
> An economy is based on two sectors, transportation and manufacturing. Production of a dollar’s worth of transportation requires an input of $0.10 from each sector and production of a dollar’s worth of manufacturing requires an input of $0.40 from each se
> The sum of the elements in a column of any of the technology matrices in the text is less than 1. Why is this the case? Would you ever expect to find a column with a sum equal to 1? Greater than 1? How would you describe an economic system where the sum
> The technology matrix for an economy based on automobiles (A) and construction (C) is The management of these two sectors would like to set the total output level so that the final demand is always 70% of the total output. Discuss methods that could be
> Refer to Problem 28. Fill in the elements in the following technology matrix. Data from problem 28:
> Give the slope and y intercept of each line. y = 15,000 + 300x
> The technology matrix for an economy based on energy (E) and transportation (T) is (A) Find the output for each sector that is needed to satisfy a final demand of $50 million for energy and $50 million for transportation. (B) Discuss the effect on the
> Find (I – M) -1 and X.
> Find (I – M) -1 and X.
> Find (I – M) -1 and X.
> pertain to the following input–output model: Assume that an economy is based on three industrial sectors: agriculture (A), building (B), and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. Re
> pertain to the following input–output model: Assume that an economy is based on three industrial sectors: agriculture (A), building (B), and energy (E). The technology matrix M and final demand matrices (in billions of dollars) are. Fin
> As systems of linear equations without matrices.
> As systems of linear equations without matrices.
> solve each equation for x, where x represents a real number.
> solve each equation for x, where x represents a real number.
> Solve the equation for the unknown quantity. (If necessary, review sections A.7, 2.5, and 2.6.)
> solve each equation for x, where x represents a real number.
> Solve each equation for x, where x represents a real number.
> A state university system is planning to hire new faculty at the rank of lecturer or instructor for several of its two-year community colleges. The number of sections taught and the annual salary (in thousands of dollars) for each rank are given in the t
> Repeat Problem 67 if the company decides to include a 1% bonus for the sales manager in the incentive plan. Data from problem 67:
> Labor and material costs for manufacturing two guitar models are given in the table: / (A) If a total of $3,000 a week is allowed for labor and material, how many of each model should be produced each week to use exactly each of the allocations of the
> Parking fees at a zoo are $5.00 for local residents and $7.50 for all others. At the end of each day, the total number of vehicles parked that day and the gross receipts for the day are recorded, but the number of vehicles in each category is not. The fo
> Write each system as a matrix equation and solve using the inverse coefficient matrix. Use a graphing calculator or computer to perform the necessary calculations.
> Write each system as a matrix equation and solve using the inverse coefficient matrix. Use a graphing calculator or computer to perform the necessary calculations
> solve for x1 and x2..
> For n x n matrices A and B, and n x1 column matrices C, D, and X, solve each matrix equation for X. Assume that all necessary inverses exist.
> A basketball team played 21 games with a winning percentage of 81%. How many games did it lose?
> For n x n matrices A and B, and n x1 column matrices C, D, and X, solve each matrix equation for X. Assume that all necessary inverses exist.
> For n x n matrices A and B, and n x1 column matrices C, D, and X, solve each matrix equation for X. Assume that all necessary inverses exist.
> Explain why the system cannot be solved by matrix inverse methods. Discuss methods that could be used and then solve the system.
> Explain why the system cannot be solved by matrix inverse methods. Discuss methods that could be used and then solve the system.
> Explain why the system cannot be solved by matrix inverse methods. Discuss methods that could be used and then solve the system.
> The matrix equation is not solved correctly. Explain the mistake and find the correct solution. Assume that the indicated inverses exist.
> The matrix equation is not solved correctly. Explain the mistake and find the correct solution. Assume that the indicated inverses exist.
> The matrix equation is not solved correctly. Explain the mistake and find the correct solution. Assume that the indicated inverses exist.
> Write each system as a matrix equation and solve using inverses.
> Write each system as a matrix equation and solve using inverses.
> Write each system as a matrix equation and solve using inverses.
> Write each system as a matrix equation and solve using inverses.
> solve for x1 and x2.
> solve for x1 and x2.
> solve for x1 and x2.
> Find x1 and x2
> Find x1 and x2
> Find x1 and x2.
> Find x1 and x2..
> As a matrix equation of the form AX = B.
> If your state sales tax rate is 8.25%, what is the total cost of a motor scooter that sells for $1,349.95?
> As a matrix equation of the form AX = B.
> Find the matrix products. Note that each product can be found mentally, without the use of a calculator or pencil-and-paper calculations
> Find the matrix products. Note that each product can be found mentally, without the use of a calculator or pencil-and-paper calculations.
> Does the given matrix have a multiplicative inverse? Explain your answer
> Does the given matrix have a multiplicative inverse? Explain your answer.
> Find the additive inverse and the multiplicative inverse, if defined, of each real number. (If necessary, review Section A.1).
> Find the additive inverse and the multiplicative inverse, if defined, of each real number. (If necessary, review Section A.1).
> The following message was encoded with matrix C. Decode this message:
> Encode the message “ONE IF BY LAND AND TWO IF BY SEA” using matrix C.
> Use of a graphing calculator or computer. Use the 4 x 4 encoding matrix B given below. Form a matrix with 4 rows and as many columns as necessary to accommodate the message The following message was encoded with matrix B. Decode this message:
> Evaluate the expression. If the answer is not an integer, round to four decimal places. (7 + 3) !
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> Use of a graphing calculator or computer. Use the 4 x 4 encoding matrix B given below. Form a matrix with 4 rows and as many columns as necessary to accommodate the message Encode the message “SAIL FROM LISBON IN MORNING” using matrix B.
> The following message was encoded with matrix A. Decode this message:
> Encode the message “FINITE INCANTATEM” using matrix A.
> Based on your observations, if A = A-1 for a square matrix A, what is A2 ? Give a mathematical argument to support your conclusion.
> find A-1 and A2 .
> Discuss the existence of M-1 for 2 x 2 upper triangular matrices of the form. Generalize your conclusions to n x n upper triangular matrices.
> Show that (AB) -1 = B-1 A-1 for.
> Find the inverse of each matrix, if it exists.
> Find the inverse of each matrix, if it exists.
> Find the inverse of each matrix, if it exists.
> Evaluate the expression. If the answer is not an integer, round to four decimal places. 9!
> Find the inverse of each matrix, if it exists.
> Find the inverse. Note that each inverse can be found mentally, without the use of a calculator or pencil-and paper calculations.
> Find the inverse. Note that each inverse can be found mentally, without the use of a calculator or pencil-and paper calculations.
> Find the inverse of each matrix if it exists.
> Find the inverse of each matrix if it exists.
> Find the inverse of each matrix if it exists.
> Find the inverse of each matrix if it exists.
> Given M find M-1 and show that M-1 M = I.
> Given M find M-1 and show that M-1 M = I.
> Given M find M-1 and show that M-1 M = I.
> evaluate the given expression without using a calculator.
> Given M find M-1 and show that M-1 M = I.
> Given M find M-1 and show that M-1 M = I.
> Without performing any row operations, explain why each of the matrices does not have an inverse.
> Without performing any row operations, explain why each of the matrices does not have an inverse.
> Without performing any row operations, explain why each of the matrices does not have an inverse.
> Without performing any row operations, explain why each of the matrices does not have an inverse.