Question: State whether the standardized test statistic z
State whether the standardized test statistic z allows you to reject the null hypothesis. Explain your reasoning.
z = 1.631
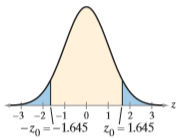
Transcribed Image Text:
-3 -2 -1 1 2 3 -Z0 = -1.645 z,- 1.645
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.01, d.f.N = 11, d.f.D = 13
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.01, d.f.N = 40, d.f.D = 60
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.05, d.f.N = 9, d.f.D = 8
> Use the TI-84 Plus displays to make a decision to reject or fail to reject the null hypothesis at the level of significance. α = 0.01 2-Test Inpt:Data Sats HO:742 g:68.1 :763 n:65 2-Test u>742 z=2.486158777 P=.0064565285 R=763 n=65 Calc
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. µ < 33
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.10, d.f.N = 15, d.f.D = 27
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic x2, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decisio
> Test the claim about the population variance σ2 or standard deviation s at the level of significance α. Assume the population is normally distributed. Claim: σ ≠ 0.035; α = 0.01. Sample statistics: s = 0.026, n = 16
> Test the claim about the population variance σ2 or standard deviation s at the level of significance α. Assume the population is normally distributed. Claim: σ = 1.25; α = 0.05. Sample statistics: s = 1.03, n = 6
> Test the claim about the population variance σ2 or standard deviation s at the level of significance α. Assume the population is normally distributed. Claim: σ2 ≤ 60; α = 0.025. Sample statistics: s2 = 72.7, n = 15
> Find the P-value for the hypothesis test with the standardized test statistic z. Decide whether to reject H0 for the level of significance α. Right-tailed test z = 2.46 α = 0.01
> Test the claim about the population variance σ2 or standard deviation s at the level of significance α. Assume the population is normally distributed. Claim: σ2 > 2; α = 0.10. Sample statistics: s2 = 2.95, n = 18
> Find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α. Left-tailed test, n = 6, α = 0.05
> Find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α. Two-tailed test, n = 41, α = 0.10
> Find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α. Two-tailed test, n = 14, α = 0.01
> Find the critical value(s) and rejection region(s) for the type of chi-square test with sample size n and level of significance α. Right-tailed test, n = 20, α = 0.05
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> Find the P-value for the hypothesis test with the standardized test statistic z. Decide whether to reject H0 for the level of significance α. Left-tailed test z = -1.55 α = 0.05
> a. identify the claim and state H0 and Ha, b. use technology to find the P-value, c. decide whether to reject or fail to reject the null hypothesis, and d. interpret the decision in the context of the original claim. Assume the population is normally
> a. identify the claim and state H0 and Ha, b. use technology to find the P-value, c. decide whether to reject or fail to reject the null hypothesis, and d. interpret the decision in the context of the original claim. Assume the population is normally
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic t, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ ≠ 3,330,000; α = 0.05. Sample statistics: x = 3,293,995, s = 12,801, n = 35
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ = 195; α = 0.10. Sample statistics: x = 190, s = 36, n = 101
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ < 850; α = 0.025. Sample statistics: x = 875, s = 25, n = 14
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ ≤ 51; α = 0.01. Sample statistics: x = 52, s = 2.5, n = 40
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ ≥ 0; α = 0.10. Sample statistics: x = -0.45, s = 2.38, n = 31
> Explain the difference between the z-test for m using a P-value and the z-test for µ using rejection region(s).
> Test the claim about the population mean µ at the level of significance α. Assume the population is normally distributed. Claim: µ > 12,700; α = 0.005. Sample statistics: x = 12,855, s = 248, n = 21
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Two-tailed test, α = 0.02, n = 12
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Left-tailed test, α = 0.005, n = 15
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Left-tailed test, α = 0.05, n = 48
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Right-tailed test, α = 0.02, n = 63
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Right-tailed test, α = 0.01, n = 33
> Find the critical value(s) and rejection region(s) for the type of t-test with level of significance α and sample size n. Two-tailed test, α = 0.05, n = 20
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the critical value(s) and identify the rejection region(s), c. find the standardized test statistic z, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision
> a. identify the claim and state H0 and Ha, b. find the standardized test statistic z, c. find the corresponding P-value, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of the original c
> You are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning. Ho: p20.73 P 0.70 0.71 0.72 a73 0.74 0.75 0.76 (a)
> a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test, a t-test, or a chi-square test. Explain your reasoning. c. Choose one of the options. Option
> a. identify the claim and state H0 and Ha, b. find the standardized test statistic z, c. find the corresponding P-value, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of the original c
> Test the claim about the population mean m at the level of significance α. Assume the population is normally distributed. Claim: µ = 7450; α = 0.10; σ = 243. Sample statistics: x = 7495, n = 27
> Test the claim about the population mean m at the level of significance α. Assume the population is normally distributed. Claim: µ < 5.500; α = 0.01; σ = 0.011. Sample statistics: x = 5.497, n = 36
> Test the claim about the population mean m at the level of significance α. Assume the population is normally distributed. Claim: µ ≠ 8.45; α = 0.03; σ = 1.75. Sample statistics: x = 7.88, n = 60
> Test the claim about the population mean m at the level of significance α. Assume the population is normally distributed. Claim: µ ≤ 45; α = 0.05; σ = 6.7. Sample statistics: x = 47.2, n = 22
> State whether the standardized test statistic z allows you to reject the null hypothesis. Explain your reasoning. z = -1.655 -3 -2 -1 1 2 3 -Z0 = -1.645 z,- 1.645
> State whether the standardized test statistic z allows you to reject the null hypothesis. Explain your reasoning. z = -1.464 -3 -2 -1 1 2 3 -Z0 = -1.645 z,- 1.645
> State whether the standardized test statistic z allows you to reject the null hypothesis. Explain your reasoning. z = 1.723 -3 -2 -1 1 2 3 -Z0 = -1.645 z,- 1.645
> Find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer. Two-tailed test, α = 0.03
> You are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning. Ho ps0.20 +++P 0.17 0.18 0.19 0.20 0.21 0.22 0.23
> Find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer. Right-tailed test, α = 0.025
> Find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer. Two-tailed test, α = 0.005
> Find the critical value(s) and rejection region(s) for the type of z-test with level of significance α. Include a graph with your answer. Left-tailed test, α = 0.02
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Find the standard err
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Find the coefficient
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Use the regression eq
> For each exercise, perform the steps below. a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning. c. Find the c
> For each exercise, perform the steps below. a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning. c. Find the c
> For each exercise, perform the steps below. a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning. c. Find the c
> For each exercise, perform the steps below. a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test or a t-test. Explain your reasoning. c. Find the c
> You are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning. Hoi uS 54 51 52 53 54 55 56 S7 (a) 53.5 <µ< 56.5 5
> In each exercise, a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision i
> In each exercise, a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision i
> In each exercise, a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision i
> In each exercise, a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision i
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Find the equation of
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Test the significance
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Calculate the correla
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Construct a scatter p
> Use the data in the table, which shows the average annual salaries (both in thousands of dollars) for secondary and elementary school teachers, excluding special and vocational education teachers, in the United States for 11 years. Construct a 95% predi
> You are given a null hypothesis and three confidence intervals that represent three samplings. Determine whether each confidence interval indicates that you should reject H0. Explain your reasoning. Ho: H2 70 67 68 9 70 71 72 73 (a) 67 <u<71 67 68 6
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. σ ≠ 5
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. µ < 128
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. µ ≤ 645
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. To support a claim, state it so that it becomes the null hypothesis.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. A large P-value in a test will favor rejection of the null hypothesis.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. The level of significance is the maximum probability you allow for rejecting a null hypothesis when it is actually true.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. If you decide to reject the null hypothesis, then you can support the alternative hypothesis.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. A statistical hypothesis is a statement about a sample.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. In a hypothesis test, you assume the alternative hypothesis is true.
> Does failing to reject the null hypothesis mean that the null hypothesis is true? Explain.
> A null hypothesis is rejected with a level of significance of 0.10. Is it also rejected at a level of significance of 0.05? Explain.
> What are the two decisions that you can make from performing a hypothesis test?
> Describe the two types of errors possible in a hypothesis test decision.
> What are the two types of hypotheses used in a hypothesis test? How are they related?
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. According to a recent survey, 52% of college students used their own income or savings to pay for college.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. According to a recent survey, 73% of college students did not use student loans to pay for college.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. An amusement park claims that the mean daily attendance at the park is at least 20,000 people.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. The standard deviation of the base price of an all-terrain vehicle is no more than $320.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. As stated by a company’s shipping department, the number of shipping errors per million shipments has a standard deviation th
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. A tablet manufacturer claims that the mean life of the battery for a certain model of tablet is more than 8 hours.
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: p = 0.25 Ha: p ≠ 0.25
> A null hypothesis is rejected with a level of significance of 0.05. Is it also rejected at a level of significance of 0.10? Explain.
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: σ2 = 142 Ha: σ2 ≠ 142
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: σ ≥ 5.2 Ha: σ < 5.2
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: µ ≤ 8.0 Ha: µ > 8.0
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ > 2 1 1 (d) 1 2
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ ≠3 1 1 (d) 1 2
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ 1 1 (d) 1 2

