Question: Suppose (1, 1) is a critical point
Suppose (1, 1) is a critical point of a function f with continuous second derivatives. In each case, what can you say about f?

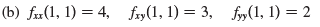
Transcribed Image Text:
(a) fæ(1, 1) = 4, fay(1, 1) = 1, fy(1, 1) = 2 (b) fæ(1, 1) = 4, fry(1, 1) = 3, fy(1, 1) = 2
> The base of an aquarium with given volume V is made of slate and the sides are made of glass. If slate costs five times as much (per unit area) as glass, find the dimensions of the aquarium that minimize the cost of the materials.
> Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is a constant c.
> Suppose f is a differentiable function of x and y, and t (u, v) = f (eu + sin v, eu + cos v). Use the table of values to calculate gu (0, 0) and tv (0, 0). f f. fy (0, 0) 6 8. (1, 2) 3 5 4. 2. 3.
> Find the dimensions of the rectangular box with largest volume if the total surface area is given as 64 cm2.
> Find the volume of the largest rectangular box in the first octant with three faces in the coordinate planes and one vertex in the plane x + 2y + 3z = 6.
> Assume that all the given functions are differentiable. If z =[f(ax + y) + g(ax – y)], show that y a? a у? ду
> Assume that all the given functions are differentiable. If z =-[f(x – y) + g(x + y)], show that () - az x²- dy
> Assume that all the given functions are differentiable. If u = f (x, y), where x = es cos t and y = es sin t, show that 2 2 ди du ди + ду no ди no no ax ds at
> A sound with frequency fs is produced by a source traveling along a line with speed vs. If an observer is traveling with speed vo along the same line from the opposite direction toward the source, then the frequency of the sound heard by the observer is
> A manufacturer has modeled its yearly production function P (the value of its entire production, in millions of dollars) as a Cobb-Douglas function P (L, K) = 1.47L0.65K0.35 where L is the number of labor hours (in thousands) and K is the invested capi
> The pressure of 1 mole of an ideal gas is increasing at a rate of 0.05 kPa/s and the temperature is increasing at a rate of 0.15 K/s. Use the equation PV = 8.31T in Example 2 to find the rate of change of the volume when the pressure is 20 kPa and the te
> Let R(s, t) = G(u((, t), v(s, t)), where G, u, and v are differentiable, u(1, 2) = 5, us(1, 2) = 4, ut(1, 2) = -3, v(1, 2) = 7, vs(1, 2) = 2, vt(1, 2) = 6, Gu(5, 7) = 9, Gv (5, 7) = -2. Find Rs (1, 2) and Rt (1, 2).
> The second directional derivative of f (x, y) is Dåf(x, y) = Da[Du f(x, y)] (. ), calculate If f(x, y) = x³ + 5x²y + y³ and u = Då f(2, 1).
> The radius of a right circular cone is increasing at a rate of 1.8 in/s while its height is decreasing at a rate of 2.5 in/s. At what rate is the volume of the cone changing when the radius is 120 in. and the height is 140 in.?
> Show that the operation of taking the gradient of a function has the given property. Assume that u and v are differentiable functions of x and y and that a, b are constants. (a). ∆ (au + bv) = a ∆u + b âˆ
> Suppose that over a certain region of space the electrical potential V is given by V (x, y, z) − 5x2 - 3xy + xyz. (a) Find the rate of change of the potential at P (3, 4, 5) in the direction of the vector v = i + j - k. (b). In which direction does V cha
> The temperature at a point (x, y, z) is given by where T is measured in 0C and x, y, z in meters. (a). Find the rate of change of temperature at the point P (2, -1, 2) in the direction toward the point (3, -3, 3). (b). In which direction does the tempe
> The temperature T in a metal ball is inversely proportional to the distance from the center of the ball, which we take to be the origin. The temperature at the point (1, 2, 2) is 1200. (a). Find the rate of change of T at (1, 2, 2) in the direction towar
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = x* – 2x?
> Use Equation 6 to find dy/dx. Equation 6: ey sin x = x + xy aF dy F. dx F,
> Use Equation 6 to find dy/dx. Equation 6: tan-1(x2y) = x + xy2 aF dy F. dx F,
> Find the directions in which the directional derivative of f (x, y) = x2 + xy3 at the point (2, 1) has the value 2.
> Use Equation 6 to find dy/dx. Equation 6: y cos x = x2 + y2 aF dy F. dx F,
> Find the maximum rate of change of f at the given point and the direction in which it occurs. f (p, q, r) = arctan (pqr), (1, 2, 1)
> Find the maximum rate of change of f at the given point and the direction in which it occurs. f (x, y, z) = x/ (y + z), (8, 1, 3)
> Find the maximum rate of change of f at the given point and the direction in which it occurs. f(x, y, z) = x In(yz), (1,2, )
> Find the maximum rate of change of f at the given point and the direction in which it occurs. f (x, y) = sin(xy), (1, 0)
> Find the maximum rate of change of f at the given point and the direction in which it occurs. f (s, t) = test, (0, 2)
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = x³ + y³ –
> Find the directional derivative of f (x, y, z) = xy2z3 at P (2, 1, 1) in the direction of Q (0, -3, 5).
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. _f(x, y) = y² – 2y
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = (x² + y)e
> Find the directional derivative of the function at the given point in the direction of the vector v. h (r, s, t) = ln (3r + 6s + 9t), (1, 1, 1), v = 4i + 12j + 6k
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = xye-&²+y³
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f (x, y) = ex cos y
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f (x, y) = y cos x
> Find the directional derivative of the function at the given point in the direction of the vector v. g(s, t) = s Jī, (2,4), v= 2i – j
> Find the directional derivative of the function at the given point in the direction of the vector v. f(x, y) — е'sin y, (0, п/3), v%3 (-6, 8)
> (a). Find the gradient of f. (b). Evaluate the gradient at the point P. (c). Find the rate of change of f at P in the direction of the vector u. f(x, y) = x² In y, P(3, 1), u = -i + Bj
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) — х3 — Зх +
> (a). Find the gradient of f . (b). Evaluate the gradient at the point P. (c). Find the rate of change of f at P in the direction of the vector u. f(x, y) %3D х/у, Р(2, 1), u = +
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = x² + xy +
> A table of values for the wind-chill index W = f (T, v) is given in Exercise 14.3.3 on page 923. Use the table to estimate the value of Du f (-20, 30), where u = (i + j)/ 2 . Table from Exercise 14.3.3: Wind speed (km/h) | 20 30 40 50 60 70 T -10 -
> Suppose (0, 2) is a critical point of a function t with continuous second derivatives. In each case, what can you say about t? (a) g:(0, 2) = –1, 9zy(0, 2) = 6, „(0, 2) = 1 (b) gr(0, 2) = –1, gry(0, 2) = 2, gry(0, 2) = –8 %3D (c) gx(0, 2) = 4, 9zy(0
> Use the Chain Rule to find dz/dt or dw/dt. z = xy3 - x2y, x = t2 + 1, y = t2 - 1
> (a). Find the gradient of f. (b). Evaluate the gradient at the point P. (c). Find the rate of change of f at P in the direction of the vector u. f(x, y, z) = x²yz – xyz', P(2, –1,1), u = (0, §, –})
> Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. u = f (x, y), where x = x (r, s, t), y = y (r, s, t).
> Find the equation of the tangent plane to the hyperboloid x2/a2 + y2/b2 - z2/c2 = 1 at (x0, y0, z0 ) and express it in a form similar to the one in Exercise 51. Exercise: Show that the equation of the tangent plane to the ellipsoid x2/a2 + y2/b2 + z2/c
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = 2 – x* +
> Most fraud perpetrators have a long history of dishonesty and deceit.
> Because fraud prevention programs are so costly, despite being ethically superior, they almost always result in higher costs and thus lower net income than using only a strong system of fraud detection.
> Because complete fraud prevention is impossible because it requires changing actual human behavior, successful companies should forgo fraud prevention and instead focus on strong fraud detection programs
> In order to create a culture of honesty and confidentiality, persons aware of fraudulent activity should be encouraged to tell only the CEO.
> Criminal conviction is much more difficult to achieve than a civil judgment because there must be proof “beyond a reasonable doubt" that the perpetrator intentionally stole assets.
> Studies show that a positive and honest work culture in a company does little to prevent fraud
> Organizations often want to avoid embarrassment and expense, so they terminate fraudulent employees without having them prosecuted further.
> The three elements of the fraud triangle by which the investigative techniques are often classified are 1. the theft act, 2. concealment efforts, and 3. conversion methods.
> Fraud is difficult to detect because some fraud symptoms often cannot be differentiated from non-fraud factors that appear to be symptoms.
> Frauds typically start large and get smaller as the perpetrator tries to conceal his dishonest acts.
> The net worth method is rarely, if ever, helpful in actual fraud investigations.
> Expectations about punishment must be communicated randomly among work groups if fraud is to be prevented.
> Effective hiring policies that discriminate between marginal and highly ethical individuals contribute to an organization's success in preventing fraud.
> Creating an expectation of punishment causes firm morale to deteriorate and often results in lower productivity.
> Not all possible controls should be implemented; rather, one must assess a control's cost and benefits before implementation.
> The major role of employee assistance programs is to help employees recover from the damaging psychological effects of fraud.
> Tips and complaints are the most common way fraud is detected.
> Even with the right opportunity or significant pressure, most people would probably not steal or embezzle.
> Most investigators rely heavily on interviews to obtain the truth.
> Once predication is present, an investigation is usually undertaken to determine whether or not fraud is actually occurring.
> If a perpetrator is not caught, his confidence in the scheme will decrease, and he will become less and less greedy.
> Several publicly available databases provide information that can be helpful in investigations.
> Organizations that want to prevent fraud must make it easy for employees and others to report suspicious activities.
> Research has shown that it is employees and managers, not auditors, who detect most frauds.
> No matter how well an organization has developed a culture of honesty and high ethics, most organizations will still have some fraud.
> Developing a positive work environment is of little importance when creating a culture of honesty.
> Fraud prevention involves two fundamental activities: 1. a hotline for tips and 2. assessing the risk of fraud and developing concrete responses to mitigate the risks and eliminate opportunities for fraud.
> Fraud prevention includes taking steps to create and maintain a culture of honesty and high ethics.
> Investigating fraud is the most cost-effective way to reduce losses from fraud.
> Legal action taken by an organization can affect the probability of whether fraud will recur.
> Physical evidence includes evidence gathered from paper, computers, and other written documents.
> Once fraud has been committed, there are no winners.
> Private credit records are maintained on both individuals and organizations by various credit-reporting companies.
> Many organizations merely dismiss dishonest employees because of the expense and time involved in prosecuting them.
> Fraud perpetrators who are prosecuted, incarcerated, or severely punished usually commit fraud again.
> Fraud can be perpetrated to benefit oneself or to benefit one's organization.
> The greater the perceived opportunity or more intense the pressure, the less rationalization it takes for someone to commit fraud.
> Effective fraud-fighters usually put most of their time and effort into minimizing the pressures for fraud perpetrators to commit fraud.
> Good internal controls will often increase opportunities for individuals to commit fraud within an organization.
> Management's example or modeling is of little importance to the control environment.
> When fraud is committed, criminal prosecution usually proceeds before civil litigation.
> A negative outcome in a civil lawsuit usually results in jail time for the perpetrator.
> In vendor fraud, customers don't pay for goods purchased.
> Counties and other local agencies that contain records are usually not very useful in fraud investigation.
> Indirect fraud occurs when a company's assets go directly into the perpetrator's pockets without the involvement of third parties.
> Companies that commit financial statement fraud are often experiencing net losses or have profits that are significantly lower than expectations.
> The three elements of the fraud triangle are a perceived pressure, a perceived opportunity, and rationalization.
> Occupational fraud is fraud committed on behalf of an organization.
> Unintentional errors in financial statements are a form of fraud.
> Fraud perpetrators are often those who are least suspected and most trusted.
> The single most critical element for a fraud to be successful is opportunity.

