Question: Suppose f is a continuous positive decreasing
Suppose f is a continuous positive decreasing function for x > 1 and an = f (n). By drawing a picture, rank the following three quantities in increasing order:
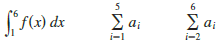
Transcribed Image Text:
5 6 °f(x) dx Σ 2 ai i-l i-2
> The function A defined by is called the Airy function after the English mathematician and astronomer Sir George Airy (1801–1892). (a). Find the domain of the Airy function. (b). Graph the first several partial sums on a common screen.
> For each predator-prey system, determine which of the variables, x or y, represents the prey population and which represents the predator population. Is the growth of the prey restricted just by the predators or by other factors as well? Do the predators
> A sequence that arises in ecology as a model for population growth is defined by the logistic difference equation Where pn measures the size of the population of the nth generation of a single species. To keep the numbers manageable, pn is a fraction o
> Determine whether the sequence converges or diverges. If it converges, find the limit. а, — 1 — (0.2)"
> Determine whether the sequence converges or diverges. If it converges, find the limit. n' + 1
> Determine whether the sequence converges or diverges. If it converges, find the limit. 3 + 5n2 a, n + n?
> Suppose that ∑∞n-1 an (an ≠ 0) is known to be a convergent series. Prove ∑∞n-1 1/an that is a divergent series.
> What is wrong with the following calculation? (Guido Ubaldus thought that this proved the existence of God because “something has been created out of nothing.”) 0 = 0 + 0 + 0 + · · . = (1 – 1) + (1 – 1) + (1 – 1)
> We know that lim n→∞ (0.8)n = 0 [from (7) with r = 0.8]. Use logarithms to determine how large has to be so that (0.8)n < 0.000001.
> In Example 7 we showed that the harmonic series is divergent. Here we outline another method, making use of the fact that ex > 1 + x for any x > 0. (See Exercise 4.3.62.) If sn is the nth partial sum of the harmonic series, show that esn > n + 1. Why doe
> Find the value of c such that ∑∞n=0 enc = 10
> The function j1 defined by is called the Bessel function of order 1. (a). Find its domain. (b). Graph the first several partial sums on a common screen. (c). If your CAS has built-in Bessel functions, graph j1 on the same screen as the partial sums in
> Find the value of c if ∑∞n-2 (1 + c)-n = 2
> Determine whether the sequence is increasing, decreasing, or not monotonic. Is the sequence bounded? a, = n +
> Determine whether the sequence is increasing, decreasing, or not monotonic. Is the sequence bounded? а, — п(-1)"
> Determine whether the sequence is increasing, decreasing, or not monotonic. Is the sequence bounded? 2n – 3 an Зп + 4
> Determine whether the sequence is increasing, decreasing, or not monotonic. Is the sequence bounded? 1 An 2n + 3
> If the nth partial sum of a series ∑∞n-1 an is sn = 3 – n2-n, find an and ∑∞n-1 an.
> If the nth partial sum of a series ∑∞n-1 an is sn = n - / n + 1 find an and ∑∞n-1 an.
> Find all values of c for which the following series converges. 1 Σ ガー」\n n +1,
> Show that if an > 0 and limn→∞ nan ≠ 0 then ∑an is divergent.
> Find all positive values of b for which the series ∑∞n=1 b ln n converges.
> Graph the first several partial sums sn(x) of the series∑∞n=0xn, together with the sum function f (x)= 1/ (1 – x), on a common screen. On what interval do these partial sums appear to be converging to f (x)?
> If ∑ an is a convergent series with positive terms, is it true that ∑ sin (an) is also convergent?
> Show that if we want to approximate the sum of the series ∑∞n=1 n-1.001 so that the error is less than 5 in the ninth decimal place, then we need to add more than 1011.301 terms!
> A series ∑an is defined by the equations Determine whether ∑an converges or diverges 2 + cos n - an an+1 aj = 1 Vn
> Is it possible to find a power series whose interval of convergence is [0, ∞]? Explain.
> A function f is defined by f (x) = 1 + 2x + x2 + 2x3 + x4 + … that is, its coefficients are c2n = 1 and c2n+1 = 2 for all n > 0. Find the interval of convergence of the series and find an explicit formula for f (x).
> Determine whether the series is absolutely convergent. ∑∞n=1 sin4n/4n
> Determine whether the series is absolutely convergent. ∑∞n=1 102/(n + 1)42n+1
> Determine whether the series is absolutely convergent. ∑∞n=1 (-1)n-12nn4
> If k is a positive integer, find the radius of convergence of the series (n!)* 00 A-0 (kn)!
> Determine whether the series is absolutely convergent. ∑∞n=1 n2/2n
> Determine whether the series is convergent or divergent. ∑∞n=1 1/√n3 + 1
> Determine whether the series is absolutely convergent. ∑∞k=1 k(2/3)k
> Find the radius of convergence and interval of convergence of the series. 2)" (3x Σ n 34 00
> Find the radius of convergence and interval of convergence of the series. 00 (x + 1)ª
> Find the radius of convergence and interval of convergence of the series. 34(х + 4) Σ 00 in
> Find the radius of convergence and interval of convergence of the series. (x – 3)" E (-1)*. 2η +1 A-0
> Find the radius of convergence and interval of convergence of the series. (-2)"x" Σ In 00 1. オー
> Find the radius of convergence and interval of convergence of the series. 00 2a Σ (-1). (2n)! n-0
> Find the radius of convergence and interval of convergence of the series. n?x" 00 E (-1)*- 2" n-1
> Test the series for convergence or divergence. ∑∞n=1 (-1)n, n /√3 + 2
> Find the radius of convergence and interval of convergence of the series. 00 n!
> Suppose that ∑∞n=0 cnxn converges when x = -4 and diverges when x= 6. What can be said about the convergence or divergence of the following series? ( a ) Σ ca A-0 (b) E ca n-0 ( c) Σ C-3)" ( d) Σ (-1)'c, 9" A-0 A-
> Find the radius of convergence and interval of convergence of the series. 00 E yn x"
> Test the series for convergence or divergence. ∑∞n=1 (-1)n-1 / 2n + 1
> Test the series for convergence or divergence. -3/4 + 5/5 – 7/6 + 9/7 – 11/8 + …
> Test the series for convergence or divergence. 4/7 – 4/8 + 4/9 – 4/10 + 4/11 - ….
> Draw a picture to show that What can you conclude about the series? Σ 1.3 -2 n 1.3
> Test the series for convergence or divergence. ∑∞n=1 (-1)n+1 n/n2 + 9
> Test the series for convergence or divergence. ∑∞n=1 (-1)n-1 / 2n + 1
> Test the series for convergence or divergence. ∑∞n=1 (-1)n-1 / ln (n + 4)
> The terms of a series are defined recursively by the equations Determine whether ∑an converges or diverges. 5n + 1 aj = 2 An+1 an 4n + 3
> If ∑∞n=0 cn4n is convergent, does it follow that the following series are convergent? (a) 2 ca(-2)ª (b) Σ c.(-4)" A-0 A-0
> What can you say about the series ∑an in each of the following cases? An+1 an+1 (а) lim an = 8 (b) lim = 0.8 an+1 (c) lim
> Determine whether the series is absolutely convergent. 2/5 + 2 ∙ 6/5 ∙ 8 + 2 ∙ 6 ∙ 10/5 ∙ 8 ∙ 11 + 2 ∙ 6 ∙ 10 ∙ 14/5 ∙ 8 ∙ 11 ∙ 14 + ∙∙∙
> Determine whether the series is absolutely convergent. 1 – 1 ∙3/3! + 1∙3∙5/5! - 1∙2∙5∙7/7!+ …+ (-1)n-1 1∙3∙5∙∙∙∙(2n – 1)/(2n – 1)!+ ∙∙∙
> Determine whether the series is absolutely convergent. ∑∞n=1 (-2)n n!/(2n)!
> Determine whether the series is absolutely convergent. ∑∞n=1 (-1)n arctan n/n2
> Determine whether the series is absolutely convergent. ∑∞n=1 (-1)n-1/√n
> Determine whether the series is absolutely convergent. ∑∞n=1 (-1)n-1 √n/n + 1
> Determine whether the series is absolutely convergent. ∑∞n=0 (-10)n/n!
> Determine whether the series is absolutely convergent. ∑∞n=1 n!/1003
> Determine whether the series is absolutely convergent. ∑∞n=1 (-3)n/n3
> Approximate the sum of the series correct to four decimal places. 00 (-1)* オー」 3"n!
> Find the radius of convergence and interval of convergence of the series. n?x" Σ 2.4. 6. ...• (2n)
> Approximate the sum of the series correct to four decimal places. (-1)*-'n? 00 10"
> Graph both the sequence of terms and the sequence of partial sums on the same screen. Use the graph to make a rough estimate of the sum of the series. Then use the Alternating Series Estimation Theorem to estimate the sum correct to four decimal places.
> Graph both the sequence of terms and the sequence of partial sums on the same screen. Use the graph to make a rough estimate of the sum of the series. Then use the Alternating Series Estimation Theorem to estimate the sum correct to four decimal places.
> Determine whether the series is convergent or divergent. ∑∞n=1 n2/n3 + 1
> Determine whether the series is convergent or divergent. ∑∞n=1 ne-n
> Determine whether the series is convergent or divergent. 1 + 1/2√2 + 1/3√3 + 14√4 + 1/5√5+ …
> For what values of p is the following series convergent? (-1)ª-1 00 nº
> Calculate the first 10 partial sums of the series and graph both the sequence of terms and the sequence of partial sums on the same screen. Estimate the error in using the 10th partial sum to approximate the total sum. (-1)^-1 ,3 ー1
> Is the 50th partial sum s50 of the alternating series ∑∞n=1(-1)n-1/n an overestimate or an underestimate of the total sum? Explain.
> Test the series for convergence or divergence. ∑∞n=1 (-1)n cos (π/n)
> Find the radius of convergence and interval of convergence of the series. x" Σ 1:3. 5. (2n – 1)
> Use the Comparison Test to determine whether the series is convergent or divergent. n Σ 2n' + 1 ,3 A-1
> Use the Integral Test to determine whether the series is convergent or divergent. 1 Σ In + 4 00 A-l V
> Use the Integral Test to determine whether the series is convergent or divergent. In
> Use the Integral Test to determine whether the series is convergent or divergent. 00 Σ ,5 A-1 n
> It is important to distinguish between and What name is given to the first series? To the second? For what values of does the first series converge? For what values of does the second series converge? Σ E nº and A-1 A-1
> Show that if an > 0 and ∑an is convergent, then ∑ ln (1 + an) is convergent.
> The meaning of the decimal representation of a number 0.d1d2d3.. (where the digit di is one of the numbers 0, 1, 2, . . . , 9) is that O.d,dzdzd4... di dz d3 da 10 104 10 102
> Suppose ∑an and ∑bn are series with positive terms and ∑bn is known to be divergent. (a). If an > bn for all n, what can you say about ∑an? Why? (b). If an < bn for all n, what can you say about ∑an? Why?
> (a). Use a graph of y = 1 to show that if sn is the nth partial sum of the harmonic series, then (b). The harmonic series diverges, but very slowly. Use part (a) to show that the sum of the first million terms is less than 15 and the sum of the first b
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. sin'n 00 n-1
> Find the radius of convergence and interval of convergence of the series. 00 2n Σ a-2 n(In n)?
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. 1 Σ Vn' + 1 00
> How many terms of the series ∑∞n=1 1/ [n (ln n)2] would you need to add to find its sum to within 0.01?
> Estimate ∑∞n=1 (2n + 1)-6 correct to five decimal places.
> Find the sum of the series ∑∞n=1 1/n5 correct to three decimal places.
> (a). Use the sum of the first 10 terms to estimate the sum of the series∑∞n=1 1/n2. How good is this estimate? (b). Improve this estimate using (4) with n = 10. (c). Find a value of that will ensure that the error in the approximation s ≈ sn is less than
> (a). Find the partial sum s10 of the series∑∞n-1 1/n4. Estimate the error in using s10 as an approximation to the sum of the series. (b). Use (4) with n = 10 to give an improved estimate of the sum. (c). Find a value of n so that sn is within 0.00001 of
> Find the values of p for which the following series is convergent. 1 Σ -2 n(ln n)P 00
> Determine whether the series is convergent or divergent. ∑∞n=1 n2 – 5n/n3 + n + 1
> List the first six terms of the sequence defined by an = n/2n + 1 Does the sequence appear to have a limit? If so, find it.
> Determine whether the series is convergent or divergent. ∑∞n=1 sin (1/n)
> Find the radius of convergence and interval of convergence of the series. n (x – a)", b>0

