Question: Suppose that the cumulative distribution function
Suppose that the cumulative distribution function of the random variable X is
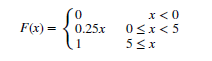
Determine the following:
a. P(X b. P(X > 1.5)
c. P(X d. P(X > 6)
> A driver’s reaction time to visual stimulus is normally distributed with a mean of 0.4 seconds and a standard deviation of 0.05 seconds. a. What is the probability that a reaction requires more than 0.5 seconds? b. What is the probability that a reaction
> The time until recharge for a battery in a laptop computer under common conditions is normally distributed with a mean of 260 minutes and a standard deviation of 50 minutes. a. What is the probability that a battery lasts more than four hours? b. What ar
> An article in Knee Surgery Sports Traumatology Arthroscopy [“Effect of Provider Volume on Resource Utilization for Surgical Procedures” (2005, Vol. 13, pp. 273–279)] showed a mean time of 129 minutes and a standard deviation of 14 minutes for anterior cr
> Assume that X is normally distributed with a mean of 10 and a standard deviation of 2. Determine the value for x that solves each of the following: a. P(X > x) = 0.5 b. P(X > x) = 0.95 c. P(x < X < 10) = 0 d. P(−x < X − 10 < x) = 0.95 e. P(−x < X − 10
> Assume that X is normally distributed with a mean of 10 and a standard deviation of 2. Determine the following: a. P(Z < 13) b. P(Z > 9) c. P(6 < X < 14) d. P(2 < X < 4) e. P(−2 < X < 8)
> A set of 200 independent patients take antiacid medication at the start of symptoms, and 80 experience moderate to substantial relief within 90 minutes. Historically, 30% of patients experience relief within 90 minutes with no medication. If the medicati
> An article in Financial Markets Institutions and Instruments [“Pricing Reinsurance Contracts on FDIC Losses” (2008, Vol. 17(3), pp. 225–247)] modeled average annual losses (in billions of dollars) of the Federal Deposit Insurance Corporation (FDIC) with
> An article in IEEE Transactions on Dielectrics and Electrical Insulation [“Statistical Analysis of the AC Breakdown Voltages of Ester Based Transformer Oils” (2008, Vol. 15(4), pp. 1044–1050)] used Weibull distributions to model the breakdown voltage of
> An article in Electronic Journal of Applied Statistical Analysis [“Survival Analysis of Dialysis Patients Under Parametric and Non-Parametric Approaches” (2012, Vol. 5(2), pp. 271–288)] modeled the survival time of dialysis patients with chronic kidney d
> An article in Sensors and Actuators A: Physical [“Characterization and Simulation of Avalanche PhotoDiodes for Next-Generation Colliders” (2011, Vol. 172(1), pp. 181–188)] considered an avalanche photodiode (APD) to detect charged particles in a photo. T
> The geometric random variable X has probability distribution f (x) = (1 − p)x−1p, x = 1, 2,… a. Show that the moment-generating function is b. Use MX(t) to find the mean and variance of X.
> An article in Proceedings of the 33rd International ACM SIGIR Conference on Research and Development in Information Retrieval [“Understanding Web Browsing Behaviors Through Weibull Analysis of Dwell Time” (2010, pp. 379–386)] proposed that a Weibull dist
> Suppose that X has a Weibull distribution with β = 2 and δ = 8.6. Determine the following: a. P(X < 10) b. P(X > 9) c. P(8 < X < 11) d. Value for x such that P(X > x) = 0.9
> Suppose that the lifetime of a component (in hours) is modeled with a Weibull distribution with β = 2 and δ = 4000. Determine the following in parts (a) and (b): a. P(X > 5000) b. P(X > 8000 | X > 3000) c. Comment on the probabilities in the previous par
> An article in the Journal of the Indian Geophysical Union titled “Weibull and Gamma Distributions for Wave Parameter Predictions” (2005, Vol. 9, pp. 55–64) described the use of the Weibull distribution to model ocean wave heights. Assume that the mean wa
> An article in the Journal of Geophysical Research [“Spatial and Temporal Distributions of U.S. Winds and Wind Power at 80 m Derived from Measurements” (2003, Vol. 108)] considered wind speed at stations throughout the United States. For a station at Amar
> Assume that the life of a roller bearing follows a Weibull distribution with parameters β = 2 and δ = 10,000 hours. a. Determine the probability that a bearing lasts at least 8000 hours. b. Determine the mean time until failure of a bearing. c. If 10 bea
> The life (in hours) of a magnetic resonance imaging machine (MRI) is modeled by a Weibull distribution with parameters β = 2 and δ = 500 hours. Determine the following: a. Mean life of the MRI b. Variance of the life of the MRI c. Probability that the MR
> Suppose that X has a Weibull distribution with β = 0.2 and δ = 100 hours. Determine the following: a. P(X < 10,000) b. P(X > 5000) c. E(X) and V(X)
> If X is a Weibull random variable with β = 1 and δ = 1000, what is another name for the distribution of X, and what is the mean of X?
> An acticle in Biometrics [“Integrative Analysis of Transcriptomic and Proteomic Data of Desulfovibrio Vulgaris: A Nonlinear Model to Predict Abundance of Undetected Proteins” (2009, Vol. 25(15), pp. 1905–1914)] reported that protein abundance from an ope
> Use integration by parts to show that Γ(r) = (r −1) Γ(r − 1).
> An article in Atmospheric Chemistry and Physics [“Relationship Between Particulate Matter and Childhood Asthma—Basis of a FutureWarning System for Central Phoenix” (2012, Vol. 12, pp. 2479–2490)] linked air quality to childhood asthma incidents. The stud
> Phoenix water is provided to approximately 1.4 million people who are served through more than 362,000 accounts (http://phoenix.gov/WATER/wtrfacts.html). All accounts are metered and billed monthly. The probability that an account has an error in a month
> Hits to a high-volumeWeb site are assumed to follow a Poisson distribution with a mean of 10,000 per day. Approximate each of the following: a. Probability of more than 20,000 hits in a day. b. Probability of less than 9900 hits in a day. c. Value such t
> The manufacturing of semiconductor chips produces 2% defective chips. Assume that the chips are independent and that a lot contains 1000 chips. Approximate the following probabilities: a. More than 25 chips are defective. b. Between 20 and 30 chips are d
> There were 49.7 million people with some type of long-lasting condition or disability living in the United States in 2000. This represented 19.3 percent of the majority of civilians aged five and over (http://factfinder.census.gov). A sample of 1000 pers
> Suppose that X is a Poisson random variable with λ = 6. a. Compute the exact probability that X is less than four. b. Approximate the probability that X is less than four and compare to the result in part (a). c. Approximate the probability that 8 < X <
> The number of (large) inclusions in cast iron follows a Poisson distribution with a mean of 2.5 per cubic millimeter. Approximate the following probabilities: a. Determine the mean and standard deviation of the number of inclusions in a cubic centimeter
> Cabs pass your workplace according to a Poisson process with a mean of five cabs per hour. a. Determine the mean and standard deviation of the number of cabs per 10-hour day. b. Approximate the probability that more than 65 cabs pass within a 10-hour day
> Suppose that X is a binomial random variable with n = 200 and p = 0.4. Approximate the following probabilities: a. P(X ≤ 70) b. P(70 < X < 90) c. P(X = 80)
> In Exercise 5.2.7, the monthly demand for MMR vaccine was assumed to be approximately normally distributed with a mean and standard deviation of 1.1 and 0.3 million doses, respectively. Suppose that the demands for different months are independent, and l
> Patients arrive at a hospital emergency department according to a Poisson process with a mean of 6.5 per hour. a. What is the mean time until the 10th arrival? b. What is the probability that more than 20 minutes is required for the third arrival?
> The rate of return of an asset is the change in price divided by the initial price (denoted as r). Suppose that $10,000 is used to purchase shares in three stocks with rates of returns X1, X2, X3. Initially, $2500, $3000, and $4500 are allocated to each
> A U-shaped component is to be formed from the three parts A, B, and C. See Figure 5.14. The length of A is normally distributed with a mean of 10 mm and a standard deviation of 0.1 mm. The thicknesses of parts B and C are each normally distributed with a
> Assume that the weights of individuals are independent and normally distributed with a mean of 160 pounds and a standard deviation of 30 pounds. Suppose that 25 people squeeze into an elevator that is designed to hold 4300 pounds. a. What is the probabil
> An automated filling machine fills soft-drink cans, and the standard deviation is 0.5 fluid ounce. Assume that the fill volumes of the cans are independent, normal random variables. a. What is the standard deviation of the average fill volume of 100 cans
> An article in Knee Surgery Sports Traumatology, Arthroscopy [“Effect of Provider Volume on Resource Utilization for Surgical Procedures” (2005, Vol. 13, pp. 273–279)] showed a mean time of 129 minutes and a standard deviation of 14 minutes for ACL recons
> Making handcrafted pottery generally takes two major steps: wheel throwing and firing. The time of wheel throwing and the time of firing are normally distributed random variables with means of 40 minutes and 60 minutes and standard deviations of 2 minute
> In the manufacture of electroluminescent lamps, several different layers of ink are deposited onto a plastic substrate. The thickness of these layers is critical if specifications regarding the final color and intensity of light are to be met. Let X and
> Suppose that the random variable X represents the length of a punched part in centimeters. Let Y be the length of the part inmillimeters. If E(X) = 5 and V(X) = 0.25, what are the mean and variance of Y?
> X and Y are independent, normal random variables with E(X) = 2, V(X) = 5, E(Y) = 6, and V(Y) = 8. Determine the following: a. E(3X + 2Y) b. V(3X + 2Y) c. P(3X + 2Y < 18) d. P(3X + 2Y < 28)
> In a data communication system, several messages that arrive at a node are bundled into a packet before they are transmitted over the network. Assume that the messages arrive at the node according to a Poisson process with λ = 30 messages per minute. Fiv
> For the Transaction Processing Performance Council’s benchmark in Exercise 5.1.6, let X, Y, and Z denote the average number of selects, updates, and inserts operations required for each type of transaction, respectively. Calculate the following: a. Corre
> Patients are given a drug treatment and then evaluated. Symptoms either improve, degrade, or remain the same with probabilities 0.4, 0.1, 0.5, respectively. Assume that four independent patients are treated and let X and Y denote the number of patients w
> Determine the value for c and the covariance and correlation for the joint probability mass function fXY (x, y) = c(x + y) for x = 1, 2, 3 and y = 1, 2, 3.
> Determine the covariance and correlation for the following joint probability distribution:
> Determine the cumulative distribution function for the distribution in Exercise 4.1.3.
> Determine the cumulative distribution function for the distribution in Exercise 4.1.1.
> Determine the cumulative distribution function for the random variable in Exercise 4.1.8. Use the cumulative distribution function to determine the probability that 400 < X < 500.
> Determine the cumulative distribution function for the random variable in Exercise 4.1.9. Use the cumulative distribution function to determine the probability that the waiting time is less than 1 hour.
> Determine the cumulative distribution function for the random variable in Exercise 4.1.10. Use the cumulative distribution function to determine the probability that the random variable is less than 55.
> The time between arrivals of customers at an automatic teller machine is an exponential random variable with a mean of 5 minutes. a. What is the probability that more than three customers arrive in 10 minutes? b. What is the probability that the time unt
> Consider the joint distribution in Exercise 5.1.10. Determine the following: a. fY | 2(y) b. E(Y | X = 2) c. V(Y | X = 2) d. Are X and Y independent?
> Determine the value of c that makes the function f (x, y) = c(x + y) a joint probability density function over the range 0 < x < 3 and x < y < x + 2. Determine the following: a. P(X < 1, Y < 2) b. P(1 < X < 2) c. P(Y > 1) d. P(X < 2, Y < 2) e. E(X) f.
> An article in Chemosphere [“Statistical Evaluations Reflecting the Skewness in the Distribution of TCDD Levels in Human Adipose Tissue” (1987, Vol. 16(8), pp. 2135–2140)] concluded that the levels of 2,3,7,8-TCDD (colorless persistent environmental conta
> An article in AppliedMathematics and Computation [“Confidence Intervals for Steady State Availability of a System with Exponential Operating Time and Lognormal Repair Time” (2003, Vol. 137(2), pp. 499–509)] considered the long-run availability of a syste
> An article in Journal of Hydrology [“Use of a Lognormal Distribution Model for Estimating Soil Water Retention Curves from Particle-Size Distribution Data” (2006, Vol. 323(1), pp. 325–334)] considered a lognormal distribution model to estimate water rete
> Suppose that the length of stay (in hours) at a hospital emergency department is modeled with a lognormal random variable X with θ = 1.5 and ω = 0.4. Determine the following in parts (a) and (b): a. Mean and variance b. P(X < 8) c. Comment on the differe
> An article in Health and Population: Perspectives and Issues (2000, Vol. 23, pp. 28–36) used the lognormal distribution to model blood pressure in humans. The mean systolic blood pressure (SBP) in males age 17 was 120.87 mm Hg. If the coefficient of vari
> The lifetime of a semiconductor laser has a lognormal distribution, and it is known that the mean and standard deviation of lifetime are 10,000 and 20,000, respectively. a. Calculate the parameters of the lognormal distribution. b. Determine the probabil
> Suppose that X has a lognormal distribution and that the mean and variance of X are 100 and 85,000, respectively. Determine the parameters θ and ω2 of the lognormal distribution. [Hint: Define u = exp(θ) and v = exp(ω2) and write two equations in terms o
> The length of time (in seconds) that a user views a page on a Web site before moving to another page is a lognormal random variable with parameters θ = 0.5 and ω2 = 1. a. What is the probability that a page is viewed for more than 10 seconds? b. By what
> Rawmaterials are studied for contamination. Suppose that the number of particles of contamination per pound of material is a Poisson random variable with a mean of 0.01 particle per pound. a. What is the expected number of pounds of material required to
> Suppose that X has a lognormal distribution with parameters θ = 2 and ω2 = 4. Determine the following in parts (a) and (b): a. P(X < 500) b. Conditional probability that X < 1500 given that X > 1000 c. What does the difference between the probabilities i
> Suppose that X has a lognormal distribution with parameters θ = 5 and ω2 = 9. Determine the following: a. P(X < 13,300) b. Value for x such that P(X ≤ x) = 0.95 c. Mean and variance of X
> Determine the mean and variance of the random variable in Exercise 4.1.8.
> Determine the mean and variance of the random variable in Exercise 4.1.1.
> Suppose that f (x) = 0.125x for 0 < x < 4. Determine the mean and variance of X.
> Suppose that f (x) = 1.5x2 for −1 < x < 1. Determine the mean and variance of X.
> The thickness of a conductive coating in micrometers has a density function of 600x−2 for 100 μm < x < 120 μm. a. Determine the mean and variance of the coating thickness. b. If the coating costs $0.50 per micrometer of thickness on each part, what is th
> Suppose that the probability density function of the length of computer cables is f (x) = 0.1 from 1200 to 1210 millimeters. a. Determine the mean and standard deviation of the cable length. b. If the length specifications are 1195 < x < 1205 millimeters
> Determine the mean and variance of the random variable in Exercise 4.1.10.
> Suppose that the random variables X, Y, and Z have the joint probability density function fXYZ(x, y, z) = c over the cylinder x2 + y2 < 4 and 0 < z < 4. Determine the constant c so that fXYZ(x, y, z) is a probability density function. Determine the follo
> Calls to a telephone system follow a Poisson process with a mean of five calls per minute. a. What is the name applied to the distribution and parameter values of the time until the 10th call? b. What is the mean time until the 10th call? c. What is the
> Suppose that the random variables X, Y, and Z have the joint probability density function f (x, y, z) = 8xyz for 0 < x < 1, 0 < y < 1, and 0 < z < 1. Determine the following: a. P(X < 0.5) b. P(X < 0.5, Y < 0.5) c. P(Z < 2) d. P(X < 0.5 or Z < 2) e. E(
> Suppose that the random variables X, Y, and Z have the following joint probability distribution. Determine the following: a. P(X = 2) b. P(X = 1, Y = 2) c. P(Z d. P(X = 1 or Z = 2) e. E(X) f. P(X = 1 | Y = 1) g. P(X = 1, Y = 1 | Z = 2) h. P(X = 1 | Y
> For the Transaction Processing Performance Council’s benchmark in Exercise 5.1.6, let X, Y, and Z denote the average number of selects, updates, and inserts operations required for each type of transaction, respectively. Calculate the following: a. fXYZ(
> The systolic and diastolic blood pressure values (mm Hg) are the pressures when the heart muscle contracts and relaxes (denoted as Y and X, respectively). Over a collection of individuals, the distribution of diastolic pressure is normal with mean 73 and
> An article in Clinical Infectious Diseases [“Strengthening the Supply of Routinely Administered Vaccines in the United States: Problems and Proposed Solutions” (2006, Vol. 42(3), pp. S97–S103)] reported that recommended vaccines for infants and children
> An article in Health Economics [“Estimation of the TransitionMatrix of a Discrete-TimeMarkov Chain” (2002, Vol. 11, pp. 33–42)] considered the changes in CD4 white blood cell counts from one month to
> The lengths of the minor and major axes are used to summarize dust particles that are approximately elliptical in shape. Let X and Y denote the lengths of theminor andmajor axes (inmicrometers), respectively. Suppose that fX(x) = exp (−x), 0 < x and the
> A manufacturer of electroluminescent lamps knows that the amount of luminescent ink deposited on one of its products is normally distributed with a mean of 1.2 grams and a standard deviation of 0.03 gram. Any lamp with less than 1.14 grams of luminescent
> Consider the joint distribution in Exercise 5.1.4. Determine the following: a. fY | 3(y) b. E(Y | X = 3) c. V(Y | X = 3)
> Consider the joint distribution in Exercise 5.1.1. Determine the following: a. Conditional probability distribution of Y given that X = 1.5 b. Conditional probability distribution of X that Y = 2 c. E(Y | X = 1.5) d. Are X and Y independent?
> Given the probability density function f (x) = 0.013x2e−0.01x/Γ(3), determine the mean and variance of the distribution.
> The conditional probability distribution of Y given X = x is fY|x(y) = xe−xy for y > 0, and the marginal probability distribution of X is a continuous uniform distribution over 0 to 10. a. Graph fY|x(y) = xe−xy for y > 0 for several values of x. Determin
> Thewaiting time for service at a hospital emergency department (in hours) follows a distribution with probability density function f (x) = 0.5 exp(−0.5x) for 0 < x.Determine the following: a. P(X < 0.5) b. P(X > 2) c. Value x (in hours) exceeded with pr
> The probability density function of the length of a metal rod is f (x) = 2 for 2.3 < x < 2.8 meters. a. If the specifications for this process are from 2.25 to 2.75 meters, what proportion of rods fail to meet the specifications? b. Assume that the proba
> The distance between major cracks in a highway follows an exponential distribution with a mean of 5 miles. a. What is the probability that there are no major cracks in a 10-mile stretch of the highway? b. What is the probability that there are two major
> The time between arrivals of taxis at a busy intersection is exponentially distributed with a mean of 10 minutes. a. What is the probability that you wait longer than 1 hour for a taxi? b. Suppose that you have already been waiting for 1 hour for a taxi.
> The number of stork sightings on a route in South Carolina follows a Poisson process with a mean of 2.3 per year. a. What is the mean time between sightings? b. What is the probability that there are no sightings within three months (0.25 years)? c. What
> The time between calls to a plumbing supply business is exponentially distributed with a mean time between calls of 15 minutes. a. What is the probability that there are no calls within a 30-minute interval? b. What is the probability that at least one c
> The life of automobile voltage regulators has an exponential distribution with a mean life of 6 years. You purchase a 6-year-old automobile with a working voltage regulator and plan to own it for 6 years. a. What is the probability that the voltage regul
> Suppose that the log-ons to a computer network follow a Poisson process with an average of three counts per minute. a. What is the mean time between counts? b. What is the standard deviation of the time between counts? c. Determine x such that the probab
> Suppose that X has an exponential distribution with a mean of 10. Determine the following: a. P(X < 5) b. P(X < 15 | X > 10) c. Compare the results in parts (a) and (b) and comment on the role of the lack of memory property.
> The total service time of a multistep manufacturing operation has a gamma distribution with mean 18 minutes and standard deviation 6. a. Determine the parameters λ and r of the distribution. b. Assume that each step has the same distribution for service
> Suppose that X has an exponential distribution with mean equal to 10. Determine the following: a. P(X > 10) b. P(X > 20) c. P(X < 30) d. Find the value of x such that P(X < x) = 0.95.
> An article in Vaccine [“Modeling the Effects of Influenza Vaccination of Health Care Workers in Hospital Departments” (2009, Vol. 27(44), pp. 6261–6267)] considered the immunization of healthcare workers to reduce the hazard rate of influenza virus infec
> An article in Ad Hoc Networks [“Underwater Acoustic Sensor Networks: Target Size Detection and Performance Analysis” (2009, Vol. 7(4), pp. 803–808)] discussed an underwater acoustic sensor network to monitor a given area in an ocean. The network does not

