Question: The atmospheric pressure at an altitude of
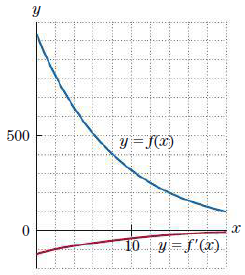
The atmospheric pressure at an altitude of x kilometers is f (x) g/cm2 (grams per square centimeter), where f (x) = 1035e-0.12x. Give approximate answers to the following questions using the graphs of f (x) and f ‘(x) shown in Fig. 2.
Figure 2:
Transcribed Image Text:
500 0 y I y = f(x) 10 y = f'(x) X
> Solve the following equations for t. t ln t = e
> Simplify the following expressions. [e ln x]2
> Simplify the following expressions. e-5 ln 1
> Simplify the following expressions. e2 ln 2
> Simplify the following expressions. ln x2 / ln x3
> Write expression in the form 2kx or 3kx, for a suitable constant k. (3-x * 3x/5)5, (161/4 * 16-3/4)3x
> Simplify the following expressions. e ln(x2)
> Compute d/dx f (g (x)), where f (x) and g (x) are: f (x) = √x, g (x) = x2 + 1
> Calculate the following. 16- 0.25
> Simplify the following expressions. e( ln 5)/2
> Solve the equation for t. Show that the tangent lines to the graph of y = (ex - e-x) / (ex + e-x) at x = 1 and x = -1 are parallel.
> Solve the equation for t. Find the equation of the tangent line to the graph of y = ex / (1 + ex) at (0,.5).
> Solve the equation for t. Determine the intervals where the function f (x) = x ln x (x > 0) is increasing and where it is decreasing.
> Solve the equation for t. Determine the intervals where the function f (x) = ln(x2 + 1) is increasing and where it is decreasing.
> Solve the equation for t. Find the points on the graph of y = ex + e-2x where the tangent line is horizontal.
> Solve the equation for t. Find the points on the graph of y = ex where the tangent line has slope 4.
> Solve the equation for t. Solve the equation 3x = 2ex.
> Write expression in the form 2kx or 3kx, for a suitable constant k. (2-3x * 2-2x)2/5, (91/2 * 94)x/9
> Compute d/dx f (g (x)), where f (x) and g (x) are: f (x) = x5, g (x) = 6x - 1
> Solve the equation for t. Solve the equation 4 * 2x = ex.
> Solve the equation for t. et - 8e0.02t = 0
> Calculate the following. 5-2
> Solve the equation for t. 4e0.03t - 2e0.06t = 0
> Show that the function in Fig. 1 has a relative maximum at x = 0 by determining the concavity of the graph at x = 0. Figure 1: f(x) = ex² - 4x² -1.5 -1-0.5 12 10 8 6 4 2 Y 0.5 1 1.5 X
> The graph of the functions f (x) = ex2 - 4x2 is shown in Fig. 1. Find the first coordinates of the relative extreme points. Figure 1: f(x) = ex² - 4x² -1.5 -1-0.5 12 10 8 6 4 2 Y 0.5 1 1.5 X
> Differentiate the following functions. y = xe
> Differentiate the following functions. y = (x2 - x + 5) / (e3x + 3)
> Differentiate the following functions. y = (√x + 1)e-2x
> Differentiate the following functions. y = eex
> Sketch the graph of y = 2/(1 + x2).
> Write expression in the form 2kx or 3kx, for a suitable constant k. 25x/4 * (1/2)x, 3-2x * 35x/2
> Differentiate the following functions. y = (ex + 1)/(x – 1)
> Differentiate the following functions. y = x ex2
> Differentiate the following functions. y = e√x
> Calculate the following. 41.5
> Differentiate the following functions. y = 10e7x
> Solve the following equations for x. e-5x * e4 = e
> Solve the following equations for x. (ex * e2)3 = e-9
> Solve the following equations for x. ex2-x = e2
> Solve the following equations for x. e-3x = e-12
> Sketch the graph of y = 4x/(x + 1)2, x >-1.
> Simplify the following. (e5x/2 - e3x) √ex
> Write expression in the form 2kx or 3kx, for a suitable constant k. 23x * 2-5x/2, 32x * (1/3)2x/3
> Simplify the following. (e8x + 7e-2x) e3x
> Simplify the following. 2x * 3x
> Simplify the following. e3x ex
> Simplify the following. e5x * e2x
> Calculate the following. 274/3
> The health expenditures (in billions of dollars) for a certain country from 1990 to 2010 are given approximately by f (t) = 27e0.106t, with time in years measured from 1990. Give approximate answers to the following questions using the graphs of f (t) an
> Use logarithmic differentiation to differentiate the function. f (x) = exx22x
> Function h(x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = √[f (x2)]
> Use logarithmic differentiation to differentiate the function. f (x) = ex+1(x2 + 1)x
> Use logarithmic differentiation to differentiate the function. f (x) = [ex √(x + 1) (x2 + 2x + 3)2]/4x2
> Write expression in the form 2kx or 3kx, for a suitable constant k. 2x/6x, 3-5x/3-2x, 16x/8-x
> Use logarithmic differentiation to differentiate the function. f (x) = [(xex)/(x3 + 3)]
> Use logarithmic differentiation to differentiate the function. f (x) = √(x2 + 5) ex2
> Use logarithmic differentiation to differentiate the function. f (x) = 10x
> Use logarithmic differentiation to differentiate the function. f (x) = x1+x
> Use logarithmic differentiation to differentiate the function. f (x) = (x2 + 5)6(x3 + 7)8(x4 + 9)10
> Use logarithmic differentiation to differentiate the function. f (x) = bx, where b > 0
> Use logarithmic differentiation to differentiate the function. f (x) = x√x
> Function h(x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = f (x2)/x
> Use logarithmic differentiation to differentiate the function. f (x) = 2x
> Use logarithmic differentiation to differentiate the function. f (x) = 5√(x5 + 1)/(x5 + 5x + 1)
> Differentiate the function. y = ln(ex + 3e-x)
> Write expression in the form 2kx or 3kx, for a suitable constant k. 4x, (√3)x, (1/9)x
> Differentiate the functions. y = (x2 + 3)(x2 - 3)10
> Differentiate the function. y = ln (1 /e√x)
> Differentiate the function. y = e2 ln(2x+1)
> Differentiate the function. y = ln |x – 1|
> Differentiate the function. y = ln(3x+1) - ln 3
> Differentiate the function. y = ln(2x)
> Function h(x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = f (f (x))
> Differentiate the function. y = ln 3√(x3 + 3x – 2)
> Differentiate the function. y = ln(ex2/x)
> Differentiate the function. y = ln |-2x + 1|
> Differentiate the function. y = ln √[(x2 + 1) / (2x + 3)]
> Differentiate the function. y = ln(x2 + ex)
> The relationship between the area of the pupil of the eye and the intensity of light was analyzed by B. H. Crawford. Crawford concluded that the area of the pupil is square millimeters when x units of light are entering the eye per unit time. (Source:
> Differentiate the function. y = ex ln x
> Differentiate the function. y = 1 / ln x
> Differentiate the function. y = ln( ln√x)
> Differentiate the function. y = e2 ln (x+1)
> Function h(x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = -f (-x)
> Differentiate the function. y = x ln x - x
> Differentiate the function. y = ln[e6x(x2 + 3)5(x3 + 1)-4]
> Differentiate the function. y = ln [xex / √(1 + x)]
> Differentiate the function. y = (x ln x)3
> Differentiate the function. y = ( ln x)2
> Differentiate the function. y = ln(9x)
> The BMI is usually used as a guideline to determine whether a person is overweight or underweight. For example, according to the Centers for Disease Control, a 12-year-old boy is at risk of being overweight if his BMI is between 21 and 24 and is consider
> Differentiate the function. y = ln (5x - 7)
> Suppose that a kitchen appliance company’s monthly sales and advertising expenses are approximately related by the equation xy - 6x + 20y = 0, where x is thousands of dollars spent on advertising and y is thousands of dishwashers sold. Currently, the com
> Animal physiologists have determined experimentally that the weight W (in kilograms) and the surface area S (in square meters) of a typical horse are related by the empirical equation S = 0.1W2/3. How fast is the surface area of a horse increasing at a t
> Function h(x) is defined in terms of a differentiable f (x). Find an expression for h (x). h(x) = 2 f (2x + 1)
> At the beginning of 1990, 20.2 million people lived in the metropolitan area of Mexico City, and the population was growing exponentially. The 1995 population was 23 million. (Part of the growth is due to immigration.) If this trend continues, how large
> An offshore oil well is leaking oil onto the ocean surface, forming a circular oil slick about .005 meter thick. If the radius of the slick is r meters, the volume of oil spilled is V = .005πr2 cubic meters. If the oil is leaking at a constant rate of 20
> Suppose that the price p and quantity x of a certain commodity satisfy the demand equation 6p + 5x + xp = 50 and that p and x are functions of time, t. Determine the rate at which the quantity x is changing when x = 4, p = 3, and dp/dt = -2.
> A town library estimates that, when the population is x thousand persons, approximately y thousand books will be checked out of the library during 1 year, where x and y are related by the equation y3 - 8000x2 = 0. (a) Use implicit differentiation to find
> A factory’s weekly production costs y and its weekly production quantity x are related by the equation y2 - 5x3 = 4, where y is in thousands of dollars and x is in thousands of units of output. (a) Use implicit differentiation to find a formula for dy/dx

