Question: The average speed of molecules in an
The average speed of molecules in an ideal gas is
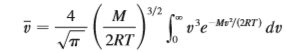
where M is the molecular weight of the gas, R is the gas constant, T is the gas temperature, and v is the molecular speed. Show that
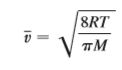
Transcribed Image Text:
3/2 v’e Mv³/(2RT") 4 M dv IT 2RT 8RT v = V TM
> The table (supplied by San Diego Gas and Electric) gives the power consumption P in megawatts in San Diego County from midnight to 6:00 am on a day in December. Use Simpson’s Rule to estimate the energy used during that time period. (Us
> Water leaked from a tank at a rate of r(t) liters per hour, where the graph of r is as shown. Use Simpson’s Rule to estimate the total amount of water that leaked out during the first 6 hours. 4 2 0 2 4 6 1 (seconds)
> The graph of the acceleration a(t) of a car measured in ft/s2 is shown. Use Simpson’s Rule to estimate the increase in the velocity of the car during the 6-second time interval. 12 8 4 4 6 t(seconds) 2.
> A radar gun was used to record the speed of a runner during the first 5 seconds of a race (see the table). Use Simpson’s Rule to estimate the distance the runner covered during those 5 seconds. t (s) v (m/s) 1 (s) v (m/
> A graph of the temperature in Boston on August 11, 2013, is shown. Use Simpson’s Rule with n = 12 to estimate the average temperature on that day. TA (F) 80 70 60- noon 4 8 4.
> The widths (in meters) of a kidney-shaped swimming pool were measured at 2-meter intervals as indicated in the figure. Use Simpson’s Rule to estimate the area of the pool. 5.6 5.0 6.8 7.2 4.8 4.8 6.2
> Estimate the area under the graph in the figure by using (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule, each with n = 6. y4 1 1 3 4 5 6 x 2.
> Find the approximations Tn, Mn, and Sn for n = 6 and 12. Then compute the corresponding errors ET, EM, and ES. (Round your answers to six decimal places. You may wish to use the sum command on a computer algebra system.) What observations can you make? I
> Find a power series representation for the function and determine the radius of convergence. f(x) = x² tan '(x')
> Find the approximations Tn, Mn, and Sn for n = 6 and 12. Then compute the corresponding errors ET, EM, and ES. (Round your answers to six decimal places. You may wish to use the sum command on a computer algebra system.) What observations can you make? I
> Find the approximations Ln, Rn, Tn, and Mn for n = 5, 10, and 20. Then compute the corresponding errors EL, ER, ET, and EM. (Round your answers to six decimal places. You may wish to use the sum command on a computer algebra system.) What observations ca
> Find the approximations Ln, Rn, Tn, and Mn for n = 5, 10, and 20. Then compute the corresponding errors EL, ER, ET, and EM. (Round your answers to six decimal places. You may wish to use the sum command on a computer algebra system.) What observations ca
> The trouble with the error estimates is that it is often very difficult to compute four derivatives and obtain a good upper bound K for / by hand. But computer algebra systems have no problem computing f (4) and graphing it, so we can easily find a value
> (a) Find the approximations T10 and M10 for / (b) Estimate the errors in the approximations of part (a). (c) How large do we have to choose n so that the approximations Tn and Mn to the integral in part (a) are accurate to within 0.0001?
> (a) Find the approximations T8 and M8 for the integral / (b) Estimate the errors in the approximations of part (a). (c) How large do we have to choose n so that the approximations Tn and Mn to the integral in part (a) are accurate to within 0.0001?
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) ( Va + x* dx, n n = 10 п
> Find a power series representation for the function and determine the radius of convergence. f(x) = In(5 – x)
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) L'In(1 'In(1 + e*) dx, n=8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) sin t dt, n = 4
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) x? dx, n = 10 O 1 + x* 1+3
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) dt, n=10 J2 In t
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Vy cos y dy, n= 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) S el 1/x dx, n п — 8 %3D
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) x'sin x dx, n= 8 Jo
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) V1 n= 4 Jo + cos x dx,
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) dx, п — 10 Jo 1 + x²
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) dx, п — 8 Jo 1 + x6
> (a) Use Equation 1 to find a power series representation for f(x) = ln(1 - x). What is the radius of convergence? (b) Use part (a) to find a power series for f(x) = x ln(1 – x). (c) By putting / in your result from part (a), express ln 2 as the sum of an
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) x - I dх, п — – 1 dx,
> Use (a) the Midpoint Rule and (b) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Compare your results to the actual value to determine the error in each approx
> Use (a) the Midpoint Rule and (b) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Compare your results to the actual value to determine the error in each approx
> Draw the graph of f(x) = sin( 1 2 ) x2 in the viewing rectangle / (a) Use the graph to decide whether L2, R2, M2, and T2 underestimate or overestimate I. (b) For any value of n, list the numbers Ln, Rn, Mn, Tn, and I in increasing order. (c) Compute L5,
> The left, right, Trapezoidal, and Midpoint Rule approximations were used to estimate / where f is the function whose graph is shown. The estimates were 0.7811, 0.8675, 0.8632, and 0.9540, and the same number of subintervals were used in each case. (a) Wh
> Show that if a > -1 and b > a + 1, then the following integral is convergent. x" 1+x*
> Find the value of the constant C for which the integral converges. Evaluate the integral for this value of C. dx ² + 13x + 1 .2
> (a) Use differentiation to find a power series representation for What is the radius of convergence? (b) Use part (a) to find a power series for (c) Use part (b) to find a power series for 1 S(x) (1 + x)* 1 S(x) (1 + x)' x? S(x)- (1 + x)'
> Find the value of the constant C for which the integral converges. Evaluate the integral for this value of C. 1 C dx x + 2 x² + 4
> Show that 0 ≤ f(t) ≤ Meat for t ≥ 0, where M and a are constants, then the Laplace transform F(s) exists for s > a.
> If f(t) is continuous for t > 0, the Laplace transform of f is the function F defined by and the domain of F is the set consisting of all numbers s for which the integral converges. Find the Laplace transforms of the following functions. F(s) = [
> Determine how large the number a has to be so that 1 -dx < 0.001 x? + 1
> Dialysis treatment removes urea and other waste products from a patient’s blood by diverting some of the blood flow externally through a machine called a dialyzer. The rate at which urea is removed from the blood (in mg/min) is often we
> Express the function as the sum of a power series by first using partial fractions. Find the interval of convergence. 2x + 3 f(x) = x? + 3x + 2
> In a study of the spread of illicit drug use from an enthusiastic user to a population of N users, the authors model the number of expected new users by the equation where c, k and are positive constants. Evaluate this integral to express in terms of c
> As we saw in Section 3.8, a radioactive substance decays exponentially: The mass at time t is / where m(0) is the initial mass and k is a negative constant. The mean life M of an atom in the substance is For the radioactive carbon isotope, 14C, used in r
> A manufacturer of lightbulbs wants to produce bulbs that last about 700 hours but, of course, some bulbs burn out faster than others. Let F(t) be the fraction of the company’s bulbs that burn out before t hours, so F(t) always lies between 0 and 1. (a) M
> Astronomers use a technique called stellar stereography to determine the density of stars in a star cluster from the observed (two-dimensional) density that can be analyzed from a photograph. Suppose that in a spherical cluster of radius R the density of
> Find the escape velocity v0 that is needed to propel a rocket of mass m out of the gravitational field of a planet with mass M and radius R. Use Newton’s Law of Gravitation and the fact that the initial kinetic energy of / supplies the needed work.
> Use the information and data in Exercise 6.4.33 to find the work required to propel a 1000-kg space vehicle out of the earth’s gravitational field. Exercise 6.4.33: (a) Newton’s Law of Gravitation states that two bod
> Find the values of p for which the integral converges and evaluate the integral for those values of p. (x' In x dx
> Express the function as the sum of a power series by first using partial fractions. Find the interval of convergence. 2x 4 f(x - х? — 4х + 3
> Find the values of p for which the integral converges and evaluate the integral for those values of p. 1 x(In x)"
> Find the values of p for which the integral converges and evaluate the integral for those values of p. dx Jo
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. sin'x
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2. sec?r xVx
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. arctan x dx Jo 2 + e*
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. x + 1 dx /x4 — х
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 1 + sin?x dx
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. dx J. x +1
> Find a power series representation for the function and determine the interval of convergence. x + a S(x). a > 0 x² + a²'
> (a) If g(x) = (sin2x)/x2 use your calculator or computer to make a table of approximate values of / for t = 2, 5, 10, 100, 1000, and 10,000. Does it appear that / is convergent? (b) Use the Comparison Theorem with f(x) = 1/x2 to show that / is convergent
> Sketch the region and find its area (if the area is finite). S = {(x, y) | –2 <x< 0, 0<y< 1//x + 2}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | 0 < x < m/2, 0 < y < sec²x}
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > 0, 0 < y< xe *}
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > 1, 0 < y< 1/(x³ + x)}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | x < 0, 0 < y< e*}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | x > 1, 0 < y<e}
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1/1 e dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. ,1/x x³
> Find a power series representation for the function and determine the interval of convergence. x - 1 x + 2 S(x)
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. cos 0 do (a/2 sin 0
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. I'r In r dr
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx x? — х — 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *w/2 ´tan?0 d0 Jo
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. /
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 6. dx Jo I - xA
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. (x + 1)?
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. '14 dx Vx + 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. e Jo dy
> Find a power series representation for the function and determine the interval of convergence. S(x) 2x? + 1
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 Je x(In x)? dx 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. zp z4 + 4
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x - dx .2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. ye » dy Зу 12
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L. zeª dz
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dv 12 v² + 2v – 3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx x² + x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. sine ecoso de Jo
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L xe * dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L( – 3y°) dy
> Find a power series representation for the function and determine the interval of convergence. x? S(x) x* + 16
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx ах V1 + x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx (x – 2)½ J3
> (a) Graph the functions f(x) = 1/x1.1 and t(x) = 1/x0.9 in the viewing rectangles [0, 10] by [0, 1] and [0, 100] by [0, 1]. (b) Find the areas under the graphs of f and t from x = 1 to x = t and evaluate for t = 10, 100, 104, 106, 1010, and 1020. (c) Fin
> Find the area under the curve y = 1/x3 from x = 1 to x = t and evaluate it for t = 10, 100, and 1000. Then find the total area under this curve for x > 1.
> Which of the following integrals are improper? Why? (a) " tan x dx (b) " tan x dx dx (c) ix? (d) fe*dx 2 – x – 2
> Explain why each of the following integrals is improper. (a) f -dx 1 1 - dx Jo 1 + x³ (b) X - (c) x'e * dx cot x dx
> The curves with equations xn + yn = 1, n = 4, 6, 8, . . . , are called fat circles. Graph the curves with n = 2, 4, 6, 8, and 10 to see why. Set up an integral for the length L2k of the fat circle with n = 2k. Without attempting to evaluate this integra
> Find the length of the curve yーfp- 13 – 1 dt 1<x< 4

