Question: The calibration test for a new weight-
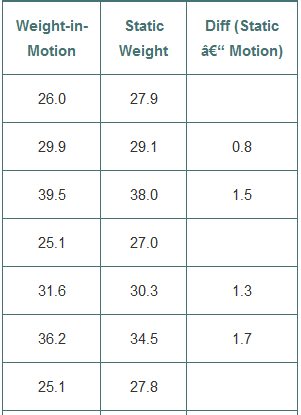
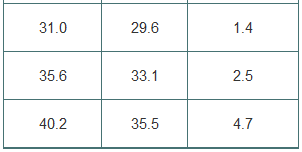
The calibration test for a new weight-in-motion method of weighing trucks was introduced in Chapter 6, exercise 52 . Is this method consistent with the traditional method of static weighing? Are the conditions for matched pairs inference satisfied? Weights are in 1000s of pounds.
> A student interested in improving her dart-throwing technique designs an experiment to test 4 different stances to see whether they affect her accuracy. After warming up for several minutes, she randomizes the order of the 4 stances, throws a dart at a t
> A student runs an experiment to study the effect of three different mufflers on gas mileage. He devises a system so that his Jeep Wagoneer uses gasoline from a one-liter container. He tests each muffler 8 times, carefully recording the number of miles he
> A figure skater tried various approaches to her Salchow jump in a designed experiment using 5 different places for her focus (arms, free leg, midsection, takeoff leg, and free). She tried each jump 6 times in random order, using two of her skating partne
> An intern from the marketing department at the Holes R Us online piercing salon has recently finished a study of the company 500 customers. He wanted to know whether the mean ZIP code of customers purchasing different products varied according to the las
> A survey of 1021 school-age children was conducted by randomly selecting children from several large urban elementary schools. Two of the questions concerned eye and hair color. In the survey, the following codes were used: The students analyzing the dat
> A researcher investigated four different word lists for use in hearing assessment. She wanted to know whether the lists were equally difficult to understand in the presence of a noisy background. To find out, she tested 96 subjects with normal hearing ra
> A student runs an experiment to test four different popcorn brands, recording the number of kernels left un-popped. She pops measured batches of each brand 4 times, using the same popcorn popper and randomizing the order of the brands. After collecting h
> Joe wants to impress his boss. He builds a regression model to predict sales that has 20 predictors and an R2 of 80%. Sally builds a competing model with only 5 predictors, but an R2 of only 78%. Which model is likely to be most useful for understanding
> In a regression to predict compensation of employees in a large firm, the predictors in the regression were Years with the Firm, Age, and Years of Experience. The coefficient of Age is negative and statistically significantly different from zero. Does th
> For each of the following cases, would your primary concern about them be that they had a large residual, large leverage, or likely large influence on the regression model? 1. In a regression to predict freshman grade point averages as part of the admiss
> Here are summary statistics for the sizes (in acres) of a collection of vineyards in the Finger Lakes region of New York State: Suppose you didn’t have access to the data. Answer the following questions from the summary statistics alone
> For each of the following cases, would your primary concern about them be that they had a large residual, large leverage, or likely large influence on the regression model? Explain your thinking. 1. In a regression to predict the construction cost of rol
> 1. Look up additional nutrition information about the BK items and combine a file holding that information with the existing BK data. 2. Define the new variable Fat/Carb as the ratio of Fat grams to Carbohydrate grams in each BK item
> 1. In the Burger King items data, use one of the variables to separate the items containing meat from the items that do not contain meat, and analyze those separately. 2. Combine data about McDonald menu items using the same variables with the data from
> Use the information in Exercise 1 to test the hypotheses H0: β1=0 vs. HA: β1‰ 0. What do you conclude about the relationship between earnings and SAT scores?
> Shoot to score, another one Returning to the results of Exercise 2, write a sentence to explain the meaning of the standard error of the slope of the regression line, SE(b1)=0.0125, and the corresponding P-value.
> Continuing with the regression of Exercise 1, write a sentence that explains the meaning of the standard error of the slope of the regression line, SE(b1)=1.545, and the corresponding P-value.
> Using the regression output from Exercise 2, identify the residual standard deviation and explain its meaning with a sentence in context.
> Using the regression output in Exercise 1, identify the residual standard deviation and explain what it means in the context of the problem.
> Discuss the assumptions and conditions necessary for proceeding with the regression analysis in Exercise 2. Do you think the conditions are satisfied?
> Discuss the assumptions and conditions necessary for proceeding with the regression analysis in Exercise 1. Do you think the conditions are satisfied?
> A survey of major universities asked what percentage of incoming freshmen usually graduate on time in 4 years. Use the summary statistics given to answer the questions that follow. 1. Would you describe this distribution as symmetric or skewed? Explain.
> A college hockey coach collected data from the 2016–2017 National Hockey League season. He hopes to convince his players that the number of shots taken has an effect on the number of goals scored. The coa
> The coach we’ve been following wants to predict how many goals each of his players will score this season. Explain why a model like the ones we’ve made won’t be very successful at doing that.
> Naturally, you would like to know what you are going to earn in the next few years. Explain why a regression model such as the ones we have found won’t do a very good job of such a prediction. (Sorry.)
> Continuing from Exercise 14, the coach responds to the players by claiming that shooting accuracy is more important than time on the ice. He adds Shoot% (% of shots on goal) to the model. Response variable is: Goals R squared=95.7% s=0.8850 with 654=61 d
> A second predictor in Exercise 13 improved the regression model of Exercise 1, so let try a third. Here a model with average ACT score of the entering class included: Response variable is: Earn R squared=36.5% s=5372 with 6874=683 degrees of freedom 1. T
> The players on the team in Exercise 2 point out to the coach that they can’t shoot if they are not on the ice. They add the variable TimeOnIce/Game (TOI/G) (in minutes per game) to the regression: (Reminder: if you are using the full da
> Continuing with the data from Exercise 1, here a regression with the percent of students who receive merit-based financial aid included in the model: Response variable is: Earn R squared=35.5% 1. Write the regression model. 2. What is the interpretation
> The coach in Exercise 2 found a 95% confidence interval for the slope of his regression line. Recall that he is trying to understand how the number of goals scored is related to shots taken. Interpret with a sentence the meaning of the interval 0.099267±
> Construct a 95% confidence interval for the slope of the regression line in Exercise 1. Interpret the meaning of the interval. Be sure to state it in the context of the data and the question about the data.
> What can the hockey coach in Exercise 2 conclude about shooting and scoring goals from the fact that the P-value < 0.0001 for the slope of the regression line? Write a sentence in context.
> A survey of 1021 school-age children was conducted by randomly selecting children from several large urban elementary schools. Two of the questions concerned eye and hair color. In the survey, the following codes were used: The statistics students analyz
> Does attending college pay back the investment? What factors predict higher earnings for graduates? Money magazine surveyed graduates, asking about their point of view of the colleges they had attended (Money Best Colleges at new.time.com/money/best-coll
> BCE Homer Iliad is an epic poem, compiled around 800 BCE, that describes several weeks of the last year of the 10-year siege of Troy (Ilion) by the Achaeans. The story centers on the rage of the great warrior Achilles. But it includes many details of inj
> For the data in Exercise 2, 1. Compute the standardized residual for each type of card. 2. Are any of these particularly large? (Compared to what?) 3. What does the answer to part b say about this new group of customers?
> For the data in Exercise 1, 1. Compute the standardized residual for each season. 2. Are any of these particularly large? (Compared to what?) 3. Why should you have anticipated the answer to part b?
> A market researcher working for the bank in Exercise 2 wants to know if the distribution of applications by card is the same for the past three mailings. She takes a random sample of 200 from each mailing and counts the number applying for Silver, Gold,
> An analyst at a local bank wonders if the age distribution of customers coming for service at his branch in town is the same as at the branch located near the mall. He selects 100 transactions at random from each branch and researches the age information
> For the customers in Exercise 2, 1. If the customers apply for the three cards according to the historical proportions, about how big, on average, would you expect the χ2 statistic to be (what is the mean of the χ2 distribution)? 2. Does the statistic
> For the births in Exercise 1, 1. If there is no seasonal effect, about how big, on average, would you expect the χ2 statistic to be (what is the mean of the χ2 distribution)? 2. Does the statistic you computed in Exercise 1 seem large in comparison to
> At a major credit card bank, the percentages of people who historically apply for the Silver, Gold, and Platinum cards are 60%, 30%, and 10%, respectively. In a recent sample of customers responding to a promotion, of 200 customers, 110 applied for Silve
> The Iliad also reports the cause of many injuries. Here is a table summarizing those reports for the 152 injuries for which the Iliad provides that information. Is there an association? 1. Under the null hypothesis, what are the expected values? 2. Compu
> Three statistics classes all took the same test. Histograms and boxplots of the scores for each class are shown below. Match each class with the corresponding boxplot.
> If there is no seasonal effect on human births, we would expect equal numbers of children to be born in each season (winter, spring, summer, and fall). A student takes a census of her statistics class and finds that of the 120 students in the class, 25 w
> Consider the weights from Exercise 4. The side-by-side boxplots below show little difference between the two groups. Should this be sufficient to draw a conclusion about the accuracy of the weigh-in-motion scale?
> Thinking about the data on fuel efficiency in Exercise 3 , why is the blocking accomplished by a matched pairs analysis particularly important for a sample that has both cars and trucks?
> Find a 98% confidence interval of the weight differences in Exercise 4 . Interpret this interval in context.
> In Exercise 3, after deleting an outlying value of –27, the mean difference in fuel efficiencies for the 632 vehicles was 7.37 mpg with a standard deviation of 2.52 mpg. Find a 95% confidence interval for this difference and interpret it in context.
> We have data on the city and highway fuel efficiency of 633 cars and trucks. 1. Would it be appropriate to use paired t methods to compare the city fuel efficiency of the cars and the trucks? 2. Would it be appropriate to use paired t methods to compare
> Which of the following scenarios should be analyzed as paired data? 1. Spouses are asked about the number of hours of sleep they get each night. We want to see if husbands get more sleep than wives. 2. 50 insomnia patients are given a placebo and 50 are
> Which of the following scenarios should be analyzed as paired data? 1. Students take an MCAT prep course. Their before and after scores are compared. 2. 20 male and 20 female students in class take a midterm. We compare their scores. 3. A group of colleg
> The researchers from Exercise 1 want to test if the proportions of foreign born are the same in the United States and Canada. What is the appropriate standard error to use for the hypothesis test? 1. What is the difference in the proportions of foreign b
> Ozone levels (in parts per billion, ppb) were recorded at sites in New Jersey monthly between 1926 and 1971. Here are boxplots of the data for each month (over the 46 years), lined up in order (January=1): 1. In what month was the highest ozone level eve
> If the information in Exercise 2 is to be used to make inferences about all people who work at non-profits and for-profit companies, what conditions must be met before proceeding? List them and explain if they are met.
> If the information in Exercise 1 is to be used to make inferences about the proportion all Canadians and all U.S. citizens born in other countries, what conditions must be met before proceeding? Are they met? Explain.
> For the interval given in Exercise 4 , explain what 95% confidence means.
> For the interval given in Exercise 3 , explain what 95% confidence means.
> The researchers from Exercise 2 created a 95% two-proportion confidence interval for the difference in those who are highly satisfied when comparing people who work at non-profits to people who work at for-profit companies. Interpret the interval with a
> The information in Exercise 1 was used to create a 95% two-proportion confidence interval for the difference between Canadians and U.S. citizens who were born in foreign countries. Interpret this interval with a sentence in context. 95% confidence  int
> Do people who work for non-profit organizations differ from those who work at for-profit companies when it comes to personal job satisfaction? Separate random samples were collected by a polling agency to investigate the difference. Data collected from 4
> The researchers in Exercise 12 decide to test the hypothesis. The degrees of freedom formula gives 51.83 df. Test the null hypothesis at α=0.05. Is the alternative one- or two-sided?
> The researchers in Exercise 11 decide to test the hypothesis that the means are equal. The degrees of freedom formula gives 162.75 df. Test the null hypothesis at α=0.05.
> Using the summary statistics provided in Exercise 12 , the sports reporter calculated the following 95% confidence interval for the mean difference between major league baseball players and professional football players. The 95% interval for μMLB−μNF
> The full series of data giving the median age at first marriage in the United States for men and women shows the following pattern. 1. In what way do these data differ from standard time series? 2. Describe the patterns you see here. 3. Do you expect the
> Using the summary statistics provided in Exercise 11 , researchers calculated a 95% confidence interval for the mean difference between Walmart and Target purchase amounts. The interval was ($14.15, $1.85). Explain in context what this interval means.
> A sports reporter suggests that professional baseball players must be, on average, older than professional football players, since football is a contact sport and players are more susceptible to concussions and serious injuries. Using data from sports.ya
> Do consumers spend more on a trip to Walmart or Target? Suppose researchers interested in this question collected a systematic sample from 85 Walmart customers and 80 Target customers by asking customers for their purchase amount as they left the stores.
> Non-profits test Complete the analysis begun in Exercise 2 . 1. What is the difference in the proportions of the two types of companies? 2. What is the value of the z-statistic? 3. What do you conclude at α=0.05?
> Suppose an advocacy organization surveys 960 Canadians and 192 of them reported being born in another country (www.unitednorthamerica.org/simdiff.htm). Similarly, 170 out of 1250 U.S. citizens reported being foreign-born. Find the standard error of the d
> Public health officials believe that 98% of children have been vaccinated against measles. A random survey of medical records at many schools across the country found that, among more than 13,000 children, only 97.4% had been vaccinated. A statistician w
> For each of the following situations, find the critical value for z or t. 1. H0:μ=105 vs. HA:μ‰ 105 at α=0.05;n=61. 2. H0:p=0.05 vs. HA:p>0.05 at α=0.05. 3. H0:p=0.6 vs. HA:p‰ 0.6 at α=0.01. 4. H0:p=0.5 vs. HA:p
> For each of the following situations, find the critical value(s) for z or t. 1. H0:p=0.5 vs. HA:p‰ 0.5 at α=0.05. 2. H0:p=0.4 vs. HA:p>0.4 at α=0.05. 3. H0:μ=10 vs. HA:μ‰ 10 at α=0.05;n=36. 4. H0:p=0.5 vs. HA:p>0.5 at α=0.01;n=345. 5. H0:μ=20 vs.
> Which of the following statements are true? If false, explain briefly. 1. It is better to use an alpha level of 0.05 than an alpha level of 0.01. 2. If we use an alpha level of 0.01, then a P-value of 0.001 is statistically significant. 3. If we use an a
> Which of the following statements are true? If false, explain briefly. 1. Using an alpha level of 0.05, a P-value of 0.04 results in rejecting the null hypothesis. 2. The alpha level depends on the sample size. 3. With an alpha level of 0.01, a P-value o
> Describe what these boxplots tell you about the relationship between the number of cylinders a car engine has and the car fuel economy (mpg).
> Which of these scatterplots show 1. little or no association? 2. a negative association? 3. a linear association? 4. a moderately strong association? 5. a very strong association?
> Which of the following are true? If false, explain briefly. 1. A very low P-value provides evidence against the null hypothesis. 2. A high P-value is strong evidence in favor of the null hypothesis. 3. A P-value above 0.10 shows that the null hypothesis
> Which of the following are true? If false, explain briefly. 1. A very high P-value is strong evidence that the null hypothesis is false. 2. A very low P-value proves that the null hypothesis is false. 3. A high P-value shows that the null hypothesis is t
> Which of the following are true? If false, explain briefly. 1. If the null hypothesis is true, you’ll get a high P-value. 2. If the null hypothesis is true, a P-value of 0.01 will occur about 1% of the time. 3. A P-value of 0.90 means that the null hypot
> For each of the following situations, state whether a Type I, a Type II, or neither error has been made. 1. A test of H0:μ=25 vs. HA:μ>25 rejects the null hypothesis. Later it is discovered that μ=24.9. 2. A test of H0:p=0.8 vs. HA:p
> For each of the following situations, state whether a Type I, a Type II, or neither error has been made. Explain briefly. 1. A bank wants to know if the enrollment on their website is above 30% based on a small sample of customers. They test H0:p=0.3 vs.
> A new reading program may reduce the number of elementary school students who read below grade level. The company that developed this program supplied materials and teacher training for a large-scale test involving nearly 8500 children in several differe
> Which of the following are true? If false, explain briefly. 1. A P-value of 0.01 means that the null hypothesis is false. 2. A P-value of 0.01 means that the null hypothesis has a 0.01 chance of being true. 3. A P-value of 0.01 is evidence against the nu
> Instead of advertising the percentage of customers who improve by at least 10 points, a manager suggests testing whether the mean score improves at all. For each customer they record the difference in score before and after taking the course (After Befor
> According to the 2010 Census, 11.4% of all housing units in the United States were vacant. A county supervisor wonders if her county is different from this. She randomly selects 850 housing units in her county and finds that 129 of the housing units are
> According to the 2010 Census, 16% of the people in the United States are of Hispanic or Latino origin. One county supervisor believes her county has a different proportion of Hispanic people than the nation as a whole. She looks at their most recent surv
> In the first 17 years of the 21st century, did men and women marry at the same age? Here are boxplots of the age at first marriage for U.S. citizens then. Write a brief report discussing what these data show.
> A test preparation company claims that more than 50% of the students who take their GRE prep course improve their scores by at least 10 points. 1. Is the alternative to the null hypothesis more naturally one-sided or two-sided? Explain. 2. A test run wit
> Referring to the study of Exercise 1: 1. Is the alternative to the null hypothesis more naturally one-sided or two-sided? Explain. 2. The P-value from a clinical trial testing the hypothesis is 0.0028. What do you conclude? 3. What would you have conclud
> As in Exercise 3, for each of the following situations, define the parameter and write the null and alternative hypotheses in terms of parameter values. 1. Seat-belt compliance in Massachusetts was 65% in 2008. The state wants to know if it has changed.
> For each of the following situations, define the parameter (proportion or mean) and write the null and alternative hypotheses in terms of parameter values. Example: We want to know if the proportion of up days in the stock market is 50%. Answer: Let p =
> A friend of yours claims to be psychic. You are skeptical. To test this you take a stack of 100 playing cards and have your friend try to identify the suit (hearts, diamonds, clubs, or spades), without looking, of course! State the null hypothesis for yo
> Developing a new drug can be an expensive process, resulting in high costs to patients. A pharmaceutical company has developed a new drug to reduce cholesterol, and it will conduct a clinical trial to compare the effectiveness to the most widely used cur
> Occasionally, a report comes out that a drug that cures some disease turns out to have a nasty side effect. For example, some antidepressant drugs may cause suicidal thoughts in younger patients. A researcher wants to study such a drug and look for evide
> The United States Golf Association (USGA) sets performance standards for golf balls. For example, the initial velocity of the ball may not exceed 250 feet per second when measured by an apparatus approved by the USGA. Suppose a manufacturer introduces a
> A researcher tests whether the mean cholesterol level among those who eat frozen pizza exceeds the value considered to indicate a health risk. She gets a P-value of 0.07. Explain in this context what the 7% represents.
> In 1960, census results indicated that the age at which American men first married had a mean of 23.3 years. It is widely suspected that young people today are waiting longer to get married. We want to find out if the mean age of first marriage has incre
> Here are boxplots of weekly gas prices for regular gas in the United States as reported by the U.S. Energy Information Administration for 2000 through 2018: 1. Compare the distribution of prices over the nineteen years. 2. Compare the stability of prices
> A very large study showed that aspirin reduced the rate of first heart attacks by 44%. A pharmaceutical company thinks they have a drug that will be more effective than aspirin, and plans to do a randomized clinical trial to test the new drug. What is th

