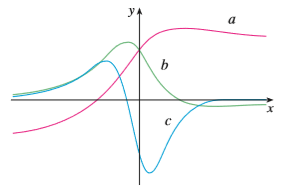
Question: The figure shows the graphs of f,
The figure shows the graphs of f, f’, and f’’. Identify each curve, and explain your choices.
Transcribed Image Text:
a b
> Prove the statement using the precise definition of a limit. lim (x? — Зx) —-2
> Prove the statement using the precise definition of a limit. lim Vx = 0 %3D
> Prove the statement using the precise definition of a limit. lim (14 – 5x) = 4
> Prove that limx → 0 x2 cos(1/x2) = 0.
> If 2x - 1 ≤ f(x) ≤ x2 for 0 < x < 3, find limx →1 f(x).
> Use graphs to discover the asymptotes of the curve. Then prove what you have discovered. y = x2 + x + 1 - x2 − x
> Use graphs to discover the asymptotes of the curve. Then prove what you have discovered. y = cos2x/x2
> Find the limit. 1 lim - 1 x? — Зх + 2
> a. Estimate the value of the limit limx→0 (1 + x)1/x to five decimal places. Does this number look familiar? b. Illustrate part (a) by graphing the function y = (1 + x)1/x.
> Find the limit. lim tan '(1/x)
> Find the limit. lim er
> Find the limit. lim (Vr2 + 4x +1– x)
> Find the limit. 1— 2х2 — х4 lim x 5 + r – 3x x*
> Find the limit. lim In(sin x)
> Find the limit. Vx2 – 9 lim 2x – 6
> Find the limit. Vx² - 9 lim x 2x - 6
> Find the limit. Vx + 6 – x lim x³ – 3x²
> Find the limit. - 1 u + 5u? — би и^ — 1 lim ,3
> Find the limit. 4 - v lim 4+ |4 – v|
> a. By graphing the function f(x) = (tan4x)/x and zooming in toward the point where the graph crosses the y-axis, estimate the value of limx→0 f(x). b. Check your answer in part (a) by evaluating f(x) for values of x that approach 0.
> Find the limit. lim 9 (r – 9)*
> Find the limit. 12 – 4 lim .3 - 8 →2
> Find the limit. (h – 1)' + 1 lim h
> Find the limit. x² – 9 lim I1t x + 2x - 3 .2
> Find the limit. x? – 9 lim .2 x-3 x + 2x - 3
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it. у.
> Match the graph of each function in (a)–(d) with the graph of its derivative in I–IV. Give reasons for your choices. (а) y. (b) (с) yA (d) yA I y4 II II IV
> Use the given graph to estimate the value of each derivative. Then sketch the graph of f’. a. f’(0) b. f’(1) c. f’(2) d. f’(3) e. f’(4) f. f&a
> Use the given graph to estimate the value of each derivative. Then sketch the graph of f’. a. f’ (-3) b. f’(-2) c. f’(-1) d. f’(0) e. f’(1) f
> Let ℓ be the tangent line to the parabola y = x2 at the point (1, 1). The angle of inclination of l is the angle ϕ that ℓ makes with the positive direction of the x-axis. Calculate ϕ correct to the nearest degree.
> Determine a. by evaluating f(x) = 1/(x3 – 1) for values of x that approach 1 from the left and from the right, b. by reasoning as in Example 9, and c. from a graph of f. 1 1 lim .3 x→1 x - 1 · and lim x→1+ x - 1
> When you turn on a hot-water faucet, the temperature T of the water depends on how long the water has been running. a. Sketch a possible graph of T as a function of the time t that has elapsed since the faucet was turned on. b. Describe how the rate of
> Nick starts jogging and runs faster and faster for 3 minutes, then he walks for 5 minutes. He stops at an intersection for 2 minutes, runs fairly quickly for 5 minutes, then walks for 4 minutes. a. Sketch a possible graph of the distance s Nick has cov
> The left-hand and right-hand derivatives off at a are defined by if these limits exist. Then f’(a) exists if and only if these one-sided derivatives exist and are equal. a. Find f’-(4) and f’+(4) f
> Recall that a function f is called even if f(-x) = f(x) for all x in its domain and odd if f(-x) = -f(x) for all such x. Prove each of the following. a. The derivative of an even function is an odd function. b. The derivative of an odd function is an e
> a. Sketch the graph of the function g(x) = x +|x|. b. For what values of x is g differentiable? c. Find a formula for g’.
> a. Sketch the graph of the function f(x) = x|x|. b. For what values of x is f differentiable? c. Find a formula for f’.
> Where is the greatest integer function f(x) = [[x]] not differentiable? Find a formula for f’ and sketch its graph.
> Show that the function f(x) =|x = 6| is not differentiable at 6. Find a formula for f’ and sketch its graph.
> a. If g(x) = x2/3, show that g’(0) does not exist. b. If a ≠ 0, find g’(a). c. Show that y = x2/3 has a vertical tangent line at (0, 0). d. Illustrate part (c) by graphing y = x2/3.
> Let f(x) = ∛x . a. If a ≠ 0, use Equation 2.7.5 to find f’(a). b. Show that f’(0) does not exist. c. Show that y = ∛x has a vertical tangent line at (0, 0). (Recall the shape of the graph of f. See Figure 1.2.13.)
> a. Find the vertical asymptotes of the function y = x2 + 1 / 3x - 2x2 b. Confirm your answer to part (a) by graphing the function.
> a. The graph of a position function of a car is shown, where s is measured in feet and t in seconds. Use it to graph the velocity and acceleration of the car. What is the acceleration at t = 10 seconds? b. Use the acceleration curve from part (a) to est
> If f(x) = 2x2 - x3, find f’(x), f’’(x), f’’’(x), and f(4)(x). Graph f, f’, f’’, and f’’’ on a common screen. Are the graphs consistent with the geometric interpretations of these derivatives?
> Use the definition of a derivative to find f’(x) and f’’(x). Then graph f, f’, and f’’ on a common screen and check to see if your answers are reasonable. f(x) = x3 - 3x
> Use the definition of a derivative to find f’(x) and f’’(x). Then graph f, f’, and f’’ on a common screen and check to see if your answers are reasonable. f(x) = 3x2 + 2x + 1
> The figure shows the graphs of four functions. One is the position function of a car, one is the velocity of the car, one is its acceleration, and one is its jerk. Identify each curve, and explain your choices. b
> The figure shows the graphs of three functions. One is the position function of a car, one is the velocity of the car, and one is its acceleration. Identify each curve, and explain your choices. a b
> The figure shows graphs of f, f’, f’’, and f’’’. Identify each curve, and explain your choices. ab c d yA
> The graphs of a function f and its derivative f’ are shown. Which is bigger, f’(-1) or f’’(1)? y
> The graphs of a function f and its derivative f’ are shown. Which is bigger, f’(-1) or f’’(1)?
> Determine the infinite limit. lim (In x² – x-2)
> Zoom in toward the points (1, 0), (0, 1), and (-1, 0) on the graph of the function g(x) = (x2 – 1)2/3. What do you notice? Account for what you see in terms of the differentiability of g.
> Graph the function f(x) = x + |x| . Zoom in repeatedly, first toward the point (-1, 0) and then toward the origin. What is different about the behavior of f in the vicinity of these two points? What do you conclude about the differentiability off?
> The graph off is given. State, with reasons, the numbers at which f is not differentiable. y4 -2 2 4
> The graph off is given. State, with reasons, the numbers at which f is not differentiable. y. 2 4 6.
> The graph off is given. State, with reasons, the numbers at which f is not differentiable. y. -2 2 4
> The graph off is given. State, with reasons, the numbers at which f is not differentiable. y. -2 2
> Suppose N is the number of people in the United States who travel by car to another state for a vacation this year when the average price of gasoline is p dollars per gallon. Do you expect dN/dp to be positive or negative? Explain.
> Let P represent the percentage of a city’s electrical power that is produced by solar panels t years after January 1, 2000. a. What does dP/dt represent in this context? b. Interpret the statement dP 3.5 dt
> Water temperature affects the growth rate of brook trout. The table shows the amount of weight gained by brook trout after 24 days in various water temperatures. If W(x) is the weight gain at temperature x, construct a table of estimated values for W&a
> The table gives the height as time passes of a typical pine tree grown for lumber at a managed site. If H(t) is the height of the tree after t years, construct a table of estimated values for H’ and sketch its graph. Tree age (yea
> Determine the infinite limit. lim In x
> The table gives the number N(t), measured in thousands, of minimally invasive cosmetic surgery procedures performed in the United States for various years t. a. What is the meaning of N’(t)? What are its units? b. Construct a table o
> The unemployment rate U(t) varies with time. The table gives the percentage of unemployed in the US labor force from 2003 to 2012. a. What is the meaning of U’(t)? What are its units? b. Construct a table of estimated values for U&aci
> a. If f(x) = x + 1/x, find f’(x). b. Check to see that your answer to part (a) is reasonable by comparing the graphs of f and f’.
> a. If f(x) = x4 + 2x, find f’(x). b. Check to see that your answer to part (a) is reasonable by comparing the graphs of f and f’.
> a. Sketch the graph of f(x) = 6 − x by starting with the graph of y = √x and using the transformations of Section 1.3. b. Use the graph from part (a) to sketch the graph of f’. c. Use the definition of a derivative to find f’(x). What are the domai
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = x4
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = x3/2
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. G(t) = 1 - 2t/3 + t
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = x2 – 1/2x - 3
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. g(x) = 9 − x
> Determine the infinite limit. 2x 8 lim x→2+ x - 5x + 6 .2
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. g(t) = 1/√t
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = x2 - 2x3
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = 4 + 8x - 5x2
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(t) = 2.5t2 + 6t
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = mx + b
> Find the derivative of the function using the definition of derivative. State the domain of the function and the domain of its derivative. f(x) = 3x - 8
> Let f(x) = x3. a. Estimate the values of f’(0), f’(1/2), f’(1), f’(2), and f’(3) by using a graphing device to zoom in on the graph of f. b. Use symmetry to deduce the values of f’(-1/2), f’(-1), f’(-2), and f’(-3). c. Use the values from parts (a) and
> Let f(x) = x2. a. Estimate the values of f’(0), f’(1/2), f’(1), and f’(2) by using a graphing device to zoom in on the graph off. b. Use symmetry to deduce the values of f’(-1 2), f’(-1), and f’(-2). c. Use the results from parts (a) and (b) to guess
> Make a careful sketch of the graph of f and below it sketch the graph of f’ in the same manner as in Exercises 4–11. Can you guess a formula for f’(x) from its graph? F(x) = ln x
> Make a careful sketch of the graph of f and below it sketch the graph of f’ in the same manner as in Exercises 4–11. Can you guess a formula for f’(x) from its graph? f(x) = ex
> Determine the infinite limit. 2x lim .2 >2 х — 4х + 4
> The point P(0.5, 0) lies on the curve y = cosπ x. a. If Q is the point (x, cosπ x), use your calculator to find the slope of the secant line PQ (correct to six decimal places) for the following values of x: i. 0 ii. 0.4 iii. 0.49 iv. 0.499 v. 1 vi
> The graph shows how the average age of first marriage of Japanese men varied in the last half of the 20th century. Sketch the graph of the derivative function M’(t). During which years was the derivative negative? 27 25 1960 1970 1
> The graph (from the US Department of Energy) shows how driving speed affects gas mileage. Fuel economy F is measured in miles per gallon and speed v is measured in miles per hour. a. What is the meaning of the derivative F’(v)? b. Ske
> A rechargeable battery is plugged into a charger. The graph shows C(t), the percentage of full capacity that the battery reaches as a function of time t elapsed (in hours). a. What is the meaning of the derivative C’(t)? b. Sketch the
> Shown is the graph of the population function P(t) for yeast cells in a laboratory culture. Use the method of Example 1 to graph the derivative P’(t). What does the graph of P’ tell us about the yeast population?
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it. y
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it.
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it. yA
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it. y4
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it. 4.
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it.
> Determine the infinite limit. lim x csc x →2m
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f’ below it.
> Find an equation of the tangent line to the curve at the given point. y = √x , (1, 1)
> Find an equation of the tangent line to the curve at the given point. y = x3 - 3x + 1, (2, 3)

