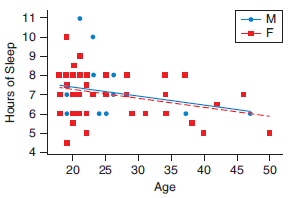
Question: The following scatterplot shows the age in

> In Exercise 4.1 there is a graph of the relationship between SAT score and college GPA. SAT score was the predictor and college GPA was the response variable. If you reverse the variables so that college GPA was the predictor and SAT score was the respon

> The table for part (a) shows distances between selected cities and the cost of a business class train ticket for travel between these cities. a. Calculate the correlation coefficient for the data shown in the table by using a computer or statistical calc

> The distance (in kilometers) and price (in dollars) for one-way airline tickets from San Francisco to several cities are shown in the table. a. Find the correlation coefficient for this data using a computer or statistical calculator. Use distance as th

> Match each of the following correlations with the corresponding graph. -0.51 _________ 0.98 _________ 0.18 _________

> Match each of the following correlations with the corresponding graph. 0.87 _________ -0.47 _________ 0.67 _________ (Source: StatCrunch: 2011 MLB Pitching Stats according to owner: IrishBlazeFighter) (Source: StatCrunch: 2011 MLB Pitching Stats accor

> Pick the letter of the graph that goes with each numerical value listed below for the correlation. Correlations: -0.903 _________ 0.374 _________ 0.777 _________

> Pick the letter of the graph that goes with each numerical value listed below for the correlation. Correlations: 0.767 _________ 0.299 _________ -0.980 ________

> Suppose you wanted to know whether ring size and height were associated. Could you do that with this data table? If so, which variables would you use?

> The scatterplot shows the acceptance rate and selectivity index for a sample of medical schools. The acceptance rate is the percentage of applicants who were accepted into the medical school. The selectivity index is a measure based on GPA, test scores,

> The first graph shows the years a person was employed before working at the company and the salary at the company. The second graph shows the years employed at the company and the salary. Which graph shows a stronger relationship and could do a better jo

> The scatterplots show SAT scores and GPA in college for a sample of students. The top graph uses the critical reading SAT score to predict GPA in college and the bottom graph shows math SAT to predict GPA. Which is the better predictor of GPA for these s

> The figure shows a scatterplot of the heights and weights of some women taking statistics. Describe what you see. Is the trend positive, negative, or near zero? Explain.

> The scatterplot shows the age and number of hours of sleep “last night” for some students. Do you think the trend is slightly positive or slightly negative? What does that mean?

> The scatterplot shows the number of hours of work per week and the number of hours of sleep per night for some college students. Does the graph show a strong increasing trend, a strong decreasing trend, or very little trend? Explain.

> The scatterplot shows the number of work hours and the number of TV hours per week for some college students who work. There is a very slight trend. Is the trend positive or negative? What does the direction of the trend mean in this context? Identify an

> Describe the trend in the scatterplot of house price and area for some houses. State which point appears to be an outlier that does not fit the rest of the data.

> The scatterplot shows the numbers of brothers and sisters for a large number of students. Do you think the trend is somewhat positive or somewhat negative? What does the direction (positive or negative) of the trend mean? Does the direction make sense in

> The scatterplot shows data on salary and years of education for a sample of workers. Comment on the trend of the scatterplot. Is the trend positive, negative, or near zero?

> Suppose you wanted to know whether living situation was associated with number of hours of study per week. Could you do that with this data table? If so, which variables would you use?

> The scatterplot shows data on credits attained and GPA for a sample of college students. Comment on the trend of the scatterplot. Is the trend positive, negative, or near zero?

> The scatterplot shows data on age and GPA for a sample of college students. Comment on the trend of the scatterplot. Is the trend positive, negative, or near zero?

> The scatterplot below shows data on age of a sample students and the number of college credits attained. Comment on the strength, direction, and shape of the trend.

> The data shows the number of calories, carbohydrates (in grams) and sugar (in grams) found in a selection of menu items at McDonald’s. Scatterplots suggest the relationship between calories and both carbs and sugars is linear. The data

> The table shows the heights (in inches) and weights (in pounds) of 14 college men. The scatterplot shows that the association is linear enough to proceed. a. Find the equation for the regression line with weight (in pounds) as the response and height (i

> The following table shows the heights and weights of some people. The scatterplot shows that the association is linear enough to proceed. a. Calculate the correlation, and find and report the equation of the regression line, using height as the predicto

> Suppose that students who scored much lower than the mean on their first statistics test were given special tutoring in the subject. Suppose that they tended to show some improvement on the next test. Explain what might cause the rise in grades other tha

> A doctor is studying cholesterol readings in his patients. After reviewing the cholesterol readings, he calls the patients with the highest cholesterol readings (the top 5% of readings in his office) and asks them to come back to discuss cholesterol-lowe

> The following figure shows the amount of money won by people playing blackjack and the amount of tips they gave to the dealer (who was a statistics student), in dollars. Would it make sense to find a correlation for this data set? Explain.

> The following figure shows information about the ages and heights of several children. Why would it not make sense to find the correlation or to perform linear regression with this data set? Explain.

> Suppose you wanted to know whether the men or the women tended to be taller. Could you do that with this data table? If so, which variables would you use?

> The following scatterplot shows the number of hours of exercise per week and the number of hours of homework per week for some students. Explain what it shows.

> The following figure shows the number of units that students were enrolled in and the number of hours (per week) that they reported studying. Do you think there is a positive trend, a negative trend, or no noticeable trend? Explain what this means about

> The figure shows a scatterplot of the wages and educational level of some people. Describe what you see. Explain the trend and mention any unusual points. (Source: www.stat.ucla.edu)

> The following figure shows a scatterplot of the educational level of twins. Describe the scatterplot. Explain the trend and mention any unusual points. (Source: www.stat.ucla.edu)

> Construct a set of numbers (with at least three points) with a strong positive correlation. Then add one point (an influential point) that changes the correlation to negative. Report the data and give the correlation of each set.

> Construct a set of numbers (with at least three points) with a strong negative correlation. Then add one point (an influential point) that changes the correlation to positive. Report the data and give the correlation of each set.

> Construct a small set of numbers with at least three points with a perfect negative correlation of -1.00.

> Construct a small set of numbers with at least three points with a perfect positive correlation of 1.00.

> Poverty rates and high school graduation rates for the 50 states and the District of Columbia are graphed below. (Source: 2017 World Almanac and Book of Facts) a. What does the trend tell us about the relationship between poverty and high school graduat

> The following scatterplot shows information about the world’s tallest 169 buildings. Stories means floors. a. What does the trend tell us about the relationship between stories and height (feet)? b. The regression line for predicting t

> Are the following variables, from Table 1A, numerical or categorical? Explain. a. Living situation b. Commute distance c. Number of aunts

> The following table gives the number of miles per gallon in the city and on the highway for some of the most fuel efficient cars according to Consumer Reports. Make a scatterplot of the data using city mileage as the predictor variable. Find the regressi

> Move studios try to predict how much money their movies will make. One possible predictor is the amount of money spent on the production of the movie. The table shows the budget and amount of money made for a sample of movies made in 2017. The budget (am

> Does education pay? The salary per year in dollars, the number of years employed (YrsEm), and the number of years of education after high school (Educ) for the employees of a company were recorded. Determine whether number of years employed or number of

> Data on the fat, carbohydrate, and calorie content for a sample of popular snack foods are found on this text’s website. Use the data to determine which is a better predictor of the number of calories in these snack foods: fat or carbohydrates?

> The LSAT is a standardized test required for entrance to most law schools. The high LSAT score for admitted students and the percentage of students passing the bar exam immediately after law school graduation for a sample of law schools is found on this

> The acceptance rate for a sample of law schools and the percentage of students employed at graduation are on this text’s website. A low acceptance rate means the law school is highly selective in admitting students. (Source: Internet Legal Research Group

> a. The following figure shows hypothetical data for a group of children. By looking at the figure, state whether the correlation between height and test score is positive, negative, or near zero. b. The shape and color of the each marker show what grade

> The following scatterplot shows the age and weight for some women. Some of them exercised regularly, and some did not. Explain what it means that the blue line (for those who did not exercise) is a bit steeper than the red line (for those who did exercis

> The scatterplot shows the shoe size and height for some men (M) and women (F). a. Why did we not extend the red line (for the women) all the way to 74 inches, instead stopping at 69 inches? b. How do we interpret the fact that the blue line is above the

> In Table 1A, there are observations on how many people?

> The following table shows the fat content (in grams) and calories for a sample of granola bars. (Source: calorielab.com) a. Use technology to make a scatterplot of the data. Use fat as the independent variable (x) and calories as the dependent variable

> In 1994, Major League Baseball (MLB) players went on strike. At the time, the average salary was $1,049,589, and the median salary was $337,500. If you were representing the owners, which summary would you use to convince the public that a strike was not

> A dieter recorded the number of calories he consumed at lunch for one week. As you can see, a mistake was made on one entry. The calories are listed in increasing order: 331, 374, 387, 392, 405, 4200 When the error is corrected by removing the extra 0, w

> When you are comparing two sets of data and one set is strongly skewed and the other is symmetric, which measures of the center and variation should you choose for the comparison?

> a. In your own words, describe to someone who knows only a little statistics how to recognize when an observation is an outlier. What action(s) should be taken with an outlier? b. Which measure of the center (mean or median) is more resistant to outliers

> The histogram shows the lengths of index fingers (in millimeters) for a sample of eighth-graders. (Source: AMSTAT Census at School) a. Use the histogram to approximate the mean ring finger length for the sample. b. Approximate the mean by completing the

> The histogram shows the lengths of ring fingers (in millimeters) for a sample of eighth-graders. (Source: AMSTAT Census at School) a. Without doing any calculations, approximate the mean finger length for the sample. b. Approximate the mean by completing

> The data at this text’s website give the heights of 18 male college students and their fathers, in inches. a. Make histograms and describe the shapes of the two data sets from the histograms. b. Fill in the following table to compare de

> Indicates cost of living for a typical consumer and is used by government economists as an economic indicator. The following data shows the CPI for large urban areas in midwestern and western states in the United States. see Guidance page 143 Midwest: W

> The following table shows the numbers of capital prisoners (prisoners on death row) in 2017 in the western U.S. states. (Source: http://www.deathpenaltyinfo.org) a. Find the median number of prisoners and interpret (using a sentence in context). b. Find

> In Table 1A, how many variables are there?

> The following table shows the numbers of capital prisoners (prisoners on death row) in 2017 in the southern U.S. states. (Source: http://www.deathpenaltyinfo. org) a. Find the median number of prisoners and interpret (using a sentence in context). b. Fin

> The following histograms show the ages of professional baseball players for two teams: the Chicago Cubs and the Oakland Athletics. a. Describe the shape of each histogram. b. Because of the shapes, which measures of center should be compared: the means o

> The following histograms show the number of years in office for Democratic and Republican U.S. senators. (Source: Infogalactic.com) a. Describe the shape of each histogram. b. Because of the shapes, what measures of center should be compared: the means o

> The National Longitudinal Survey records the heights of a representative sample of youths aged 14 to 20. The histograms show data for the heights of males and females. If you were comparing the heights of males and females, which measures of center and s

> Home prices in San Luis Obispo County for a recent month are shown in the histogram. (Source: StatCrunch) a. Describe the shape of the distribution. b. Because of the shape, what measures of center and spread should be used to describe the distribution?

> a. Report the shape of each of the following histograms b. Match each histogram with the corresponding boxplot (A, B, or C).

> The following boxplot shows the percentage of the population that has earned a bachelor’s (BA) degree in the western (W) and eastern (E) United States. Estimate and interpret the median for each group. (Source: 2017 World Almanac and Bo

> The following boxplot shows the average ticket price for professional hockey (NHL), football (NFL), basketball (NBA), and baseball (MLB) for the 2017 seasons. a. Which sport has the most expensive ticket prices? Which sport has the least expensive ticket

> The figure shows the population density (people per square mile) for the 50 states in the United States, based on an estimate from the U.S. Census Bureau. The regions are the Midwest (MW), Northeast (NE), South (S), and West (W). In the West, the potenti

> The following boxplot shows the poverty rates (the proportion of the population below the government’s official poverty level) for the 50 states and the District of Columbia. The regions are the West (W), South (S), NE (Northeast), and

> A student did a survey on the age of marriage for married male and female students. a. Is the format of the data set stacked or unstacked? b. If you answered “stacked” then unstack the data into two columns. If you an

> The five-number summary for a distribution of final exam scores is 60, 78, 80, 90, 100 Is it possible to draw a boxplot based on this information? Why or why not?

> The five-number summary for a distribution of final exam scores is 40, 78, 80, 90, 100 Explain why it is not possible to draw a boxplot based on this information. (Hint: What more do you need to know?)

> The following dotplot shows the distribution of passing rates for the bar exam law schools in the United States in. The five number summary is 0.60, 0.84, 0.90, 0.94, 1.00 Draw the boxplot and explain how you determined where the whiskers go.

> The dotplot shows the distribution of the heights (in feet) of a sample of roller coasters. The five-number summary of the data is given in the following table. Sketch a boxplot of the data. Explain how you determined the length of the whiskers.

> Data at this text’s website show the gas taxes for each of the 50 states and the District of Columbia. A summary of the data is shown in the following table. Should the maximum and minimum values of this data set be considered potential

> Data at this text’s website show the number of central public libraries in each of the 50 states and the District of Columbia. A summary of the data is shown in the following table. Should the maximum and minimum values of this data set

> Match each of the histograms (X, Y, and Z) with the corresponding boxplot (C, M, or P). Explain your reasoning.

> Name two measures of the center of a distribution, and state the conditions under which each is preferred for describing the typical value of a single data set.

> Data was collected on the industrial energy consumption per capita (in million BTUs) for all the states. A summary of the data is shown in the following table. (Source: eia.gov) Summary statistics: a. What percentage of the states consumed fewer than 47

> Data was collected on the total energy consumption per capita (in million BTUs) for all the states. A summary of the data is shown in the following table. (Source: eia.gov) Summary statistics: a. What percentage of the states consumed more than 390 mill

> A student shared data from the Stat Crunch Friend Data Application. Data on gender and number of wall posts for a sample of friends are shown below. (Source: Stat Crunch, Facebook Friend Data, posted 2/13/14) a. Is the format of this data set stacked or

> Use the data in Exercise 3.44, find and interpret the median domestic gross of the top five DC movies.

> Use the data in Exercise 3.43, find and interpret the median domestic gross of the top seven Marvel movies.

> The top seven movies based on DC comic book characters for the U.S. box office as of fall 2017 are shown in the following table, rounded to the nearest hundred million. (Source: ultimatemovieranking.com) a. Find and interpret the median in context. b. Fi

> The top ten movies based on Marvel comic book characters for the U.S. box office as of fall 2017 are shown in the following table, with domestic gross rounded to the nearest hundred million. (Source: ultimatemovieranking.com) a. Sort the domestic gross i

> Name two measures of the variation of a distribution, and state the conditions under which each measure is preferred for measuring the variability of a single data set.

> Data on residential energy consumption per capita (measured in million BTU) had a mean of 70.8 and a standard deviation of 7.3 for the states east of the Mississippi River. Assume that the distribution of residential energy use if approximately unimodal

> The histogram shows the number of runs scored by major league baseball teams for three seasons. The distribution is roughly unimodal and symmetric, with a mean of 687 and a standard deviation of 66 runs. An interval one standard deviation above and below

> Assume that women’s heights have a distribution that is symmetric and unimodal, with a mean of 64 inches and a standard deviation of 2.5 inches. a. What women’s height corresponds with a z-score of -1.00? b. Professional basketball player Evelyn Akhator

> Assume that men’s heights have a distribution that is symmetric and unimodal, with a mean of 69 inches and a standard deviation of 3 inches. a. What men’s height corresponds to a z-score of 2.00? b. What men’s height corresponds to a z-score of -1.50?

> Babies born after 40 weeks gestation have a mean length of 52.2 centimeters (about 20.6 inches). Babies born one month early have a mean length of 47.4 centimeters. Assume both standard deviations are 2.5 centimeters and the distributions are unimodal an

> Students who have accumulated fewer than 30 units are called Freshmen. a. Create a new categorical variable, named Freshman, that classifies each student in Table 1A as a freshman (less than 30 units) or not a freshman. Call this variable Freshman. Repor

> Babies born weighing 2500 grams (about 5.5 pounds) or less are called low-birthweight babies, and this condition sometimes indicates health problems for the infant. The mean birth weight for U.S.-born children is about 3462 grams (about 7.6 pounds). The

> Distributions of gestation periods (lengths of pregnancy) for humans are roughly bell-shaped. The mean gestation period for humans is 272 days, and the standard deviation is 9 days for women who go into spontaneous labor. Which is more unusual, a baby be

> Wechsler IQ tests have a mean of 100 and a standard deviation of 15. Which is more unusual: an IQ above 110 or an IQ below 80?

> Refer to the dotplot in the previous question. a. What is the height of a woman with a z-score of -1? b. What is the z-score for a woman who is 70 inches tall (5 feet 10 inches)?

> The dotplot shows heights of college women; the mean is 64 inches (5 feet 4 inches), and the standard deviation is 3 inches. a. What is the z-score for a height of 58 inches (4 feet 10 inches)? b. What is the height of a woman with a z-score of 1?