Question: The following table shows the average January
The following table shows the average January high temperature and the average July high temperature (in °F) for 10 major cities around the world.
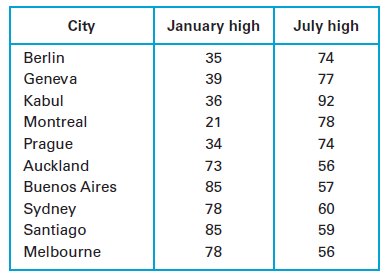
Construct a scatterplot for the data. Estimate or compute the correlation coefficient. Based on this correlation coefficient, would you conclude that January and July temperatures are correlated for these cities? Explain.
Note that the first five cities in the table are in the Northern Hemisphere and the last five are in the Southern Hemisphere. How does this change your view of the correlation? Would you now conclude that January and July temperatures are correlated for these cities? Explain.
> In testing a claim about a population mean, the t distribution is always used when the population standard deviation / is not known.
> You should always use the t distribution when the sample size is only n = 5.
> If a collection of paired sample data values yields a correlation coefficient of r = 1, then we can be very confident that causality is involved.
> If the hypothesis test of the claim described in Exercise 7 results in a P-value of 0.757, what do you conclude about the null hypothesis?
> Researchers conducted animal experiments to study smoking and lung cancer because it would have been unethical to conduct these experiments on humans.
> Describe three levels of confidence in causality that are used in the legal system, and briefly explain how these can be useful when we consider establishing causality with statistics.
> Briefly state in your own words the six guidelines that can be used in establishing causality.
> Briefly describe the correlations that made researchers suspect a link between smoking and lung cancer, and how causality was ultimately established.
> What is the difference between finding a correlation between two variables and establishing causality between two variables?
> The article “Does Vasectomy Cause Prostate Cancer?” (Chance, Vol. 10, No. 1) reports on several large studies that found an increased risk of prostate cancer among men with vasectomies. In the absence of a direct cause, several researchers attribute the
> Those who favor gun control often point to a positive correlation between the availability of handguns and the homicide rate to support their position that gun control would save lives. Does this correlation, by itself, indicate that handgun availability
> Suppose that people living near a high-voltage power line have a higher incidence of cancer than people living farther from the power line. Can you conclude that the high-voltage power line is the cause of the elevated cancer rate? If not, what other exp
> A study reported in Nature claims that women who give birth later in life tend to live longer. Of the 78women who were at least 100 years old at the time of the study, 19% had given birth after their 40th birthday. Of the 54women who were 73 years old
> A famous study in Forum on Medicine concluded that the mean lifetime of conductors of major orchestras was 73.4 years, about 5 years longer than the mean lifetime of all American males at the time. The author claimed that a life of music causes a longer
> Assume that you want to test the claim that adult males in California, New York, Colorado, and Texas have the same mean height. What method would you use to test that claim?
> Several things besides smoking have been shown to be probabilistic causal factors in lung cancer. For example, exposure to asbestos and exposure to radon gas, both of which are found in many homes, can cause lung cancer. Suppose that you meet a person wh
> There is a strong correlation between tobacco smoking and incidence of lung cancer, and most physicians believe that tobacco smoking causes lung cancer. Yet, not everyone who smokes gets lung cancer. Briefly describe how smoking could cause cancer when n
> When some people climb to higher altitudes without supplemental oxygen, they tend to experience increased physiological problems, such as headaches or disorientation. Briefly describe how the higher altitude could cause such problems when not all climber
> People who meditate more are likely to have higher incomes.
> Drinking greater amounts of alcohol decreases a person’s reaction time.
> Lower back pain can be reduced by exposing the back to a magnet.
> The time it takes to run a marathon is affected by the amount of time spent training for it.
> If causality has been established beyond reasonable doubt, then we can be 100% confident that the causality is real.
> Data showed a strong correlation between exposure to second-hand smoke and the measured amount of cotinine in the body. Follow-up experiments ruled out coincidence as an explanation for this correlation, and biologists identified a mechanism by which sec
> What is multiple regression? When is it useful?
> What type of hypothesis test would be used to test the claim in Exercise 5: left-tailed, right-tailed, or two-tailed?
> What does the square of the correlation coefficient, r2, tell us about a best-fit line?
> Briefly list five important cautions to keep in mind when making predictions with bestfit lines.
> What is a best-fit line? How is a best-fit line useful?
> a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the variation in the variable can be accoun
> a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the variation in the variable can be accoun
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> What are the null and alternative hypotheses for a claim that the mean weight of NFL professional football players is greater than 200 pounds?
> In each case, answer the following. a. How well does the best-fit line actually fit the points in the scatterplot? b. Briefly discuss the strength of the correlation. Estimate or compute r and r2. Based on your value for r 2, identify how much of the var
> In seeking to understand the factors that affect a college graduate’s future income, researchers conducted a multiple regression analysis that examined the effects of major, grade point average, the ranking of the college, parental affluence, and parenta
> Using sample data on footprint lengths and heights from men, the equation of the best-fit line is obtained, and it is used to find that a man with a footprint length of 36 inches is predicted to have a height of 144 inches, or 12 feet.
> The data barely deviate at all from the best-fit line, and they produce this value for the square of the correlation coefficient: r2 = 0.3.
> I used a best-fit line for data showing the ages and heights of thousands of boys of various ages to predict the mean height of 9-year-old boys.
> If a correlation is very strong, can we conclude that one variable causes a change in the other variable? Why or why not?
> What are the three possible explanations for a correlation?
> Briefly explain how data that actually come from two distinct groups, both with strong correlations, can appear uncorrelated when grouped together. Does this mean that you should always break data into as many subgroups as possible? Why or why not?
> Briefly explain how an outlier can make it appear that there is correlation when there is none. Also briefly explain how an outlier can make it appear that there is no correlation when there is one. Under what circumstances is it reasonable to ignore out
> The scatterplot in Figure 7.18 depicts paired data values consisting of the weight (in grams) and year of manufacture for each of 72 pennies. a. Considering the complete collection of data, does there appear to be a correlation? b. Consider the grouping
> A simple random sample of 25 blood platelet counts is obtained from a normally distributed population with an unknown standard deviation. Which of the following distributions is most appropriate for a hypothesis test involving a claim about a population
> Figure 7.17 shows the birth and death rates for different countries, measured in births and deaths per 1000 people. Estimate the correlation coefficient, and discuss whether there is a strong correlation between the two variables. Notice that there appea
> The following table lists footprint length (in centimeters) and height (in centimeters) of 10 subjects (including both men and women). Use either a scatterplot or a formula for the linear correlation coefficient to determine whether there is a correlatio
> Consider the scatterplot in Figure 7.16. Which point is an outlier? Ignoring the outlier, estimate or compute the correlation coefficient for the remaining points. Now include the outlier. How does the outlier affect the correlation coefficient? Estimate
> Consider the scatterplot in Figure 7.15. Which point is an outlier? Ignoring the outlier, estimate or compute the correlation coefficient for the remaining points. Now include the outlier. How does the outlier affect the correlation coefficient? Estimate
> Data from the Centers for Disease Control and the Department of Energy show that as the numbers of people who drown in swimming pools increases, the power generated by nuclear plants also increases.
> It has been found that when gas prices increase, the distances that vehicles are driven tend to get shorter.
> Astronomers have discovered that, with the exception of a few nearby galaxies, all galaxies in the universe are moving away from our solar system. Moreover, the farther away the galaxy is, the faster it is moving away.
> It has been found that as the number of traffic lights increases, the number of car crashes also increases.
> Data from the National Vital Statistics Reports and the U.S. Department of Agriculture show that over the past several years in Maine, the divorce rate declined and per capita margarine consumption also declined.
> For the hypothesis test described in Exercise 1, which of the following distributions is most appropriate? a. normal distribution b. t distribution c. chi-square distribution d. uniform distribution
> Statistics students find that as they spend more time studying, their test scores are higher
> One study showed that there is a correlation between per capita cheese consumption and number of people who die by becoming tangled in their bedsheets. One variable increased while the other decreased over time.
> In one state, the number of unregistered handguns steadily increased over the past several years, and the crime rate increased as well.
> The correlation I found was so strong that a careful calculation showed it had less than a 1 in 100,000 probability of occurring by chance. Therefore, I can reasonably conclude that one variable is the cause of the other.
> A study showed that for one town, as the stork population increased, the number of human births in the town also increased. It therefore follows that the increase in the stork population caused the number of births to increase.
> If a scatterplot shows no correlation, then there cannot be any relationship between the two variables.
> I created a scatterplot of CEO salaries and corporate revenue for 10 companies and found a negative correlation, but when I left out a data point for a company whose CEO took no salary, there was no correlation for the remaining data.
> Define and distinguish between positive correlation, negative correlation, and no correlation. Give an example of each type of correlation
> What is a scatterplot, and how is one constructed? How can we use a scatter plot to investigate a correlation?
> What is a correlation? Give three examples of pairs of variables that are correlated.
> As part of the results from the test described in Exercise 1, the P-value of 0.001 is obtained. What do you conclude?
> Listed below are the ages of female and male Academy Award winners in 15 selected years. Each pair of ages is for the same year. Construct a scatterplot; Briefly characterize the correlation in words (such as “strong positive correlati
> A nonprofit organization held a fund-raising auction attended by one of the authors of this text. He recorded the opening bids suggested by the auctioneer and the final winning bids for several items. The amounts (in dollars) are listed below. Construct
> Listed below are systolic blood pressure measurements (in mm Hg) obtained from the same woman (based on data from “Consistency of Blood Pressure Differences Between the Left and Right Arms,” by Eguchi, et al., Archives
> The table below lists brain sizes (in cm3) and Wechsler IQ scores of subjects (based on data from “Brain Size, Head Size, and Intelligence Quotient in Monozygotic Twins,” by Tramo etˆal., Neurology, Vol. 50
> Listed below are repair costs (in dollars) for cars crashed at 6 mi/h in full-front crash tests and the same cars crashed at 6 mi/h in full-rear crash tests (based on data from the Insurance Institute for Highway Safety). The cars are the Toyota Camry, M
> Listed below are altitudes (in thousands of feet) and outside air temperatures (in °F) recorded by one of the authors of this text during Delta Flight 1053 from New Orleans to Atlanta. Construct a scatterplot; Briefly characterize the correla
> Listed below are numbers of enrolled students (in thousands) and numbers of campus burglaries for randomly selected large colleges in a recent year (based on data from the New York Times). Construct a scatterplot; Briefly characterize the correlation in
> Listed below are annual data for various years. The data are weights (metric tons) of lemons imported from Mexico and U.S. car crash fatality rates per 100,000 population [based on data from “The Trouble with QSAR (or How I Learned to S
> Because the same sample values are used, the correlation coefficient remains unchanged if we rearrange the order of the x-values that are paired with the y-values.
> The correlation coefficient remains unchanged if we change the sign of all of the x-values.
> If the hypothesis test described in Exercise 9 results in a P-value of 0.001, what do you conclude about the null hypothesis?
> The correlation coefficient remains unchanged if we multiply all of the values of x by the same positive constant.
> The correlation coefficient remains unchanged if we interchange the variables x and y.
> Figure 7.8 shows a scatter plot in which the actual high temperature for the day is compared with a forecast made two days in advance. Estimate the correlation coefficient, and discuss what these data imply about weather forecasts. Do you think you would
> One classic example of a correlation involves the association between the temperature and the number of times a cricket chirps in a minute. The scatter plot in Figure 7.7 on the next page shows the relationship for eight different pairs of values of temp
> The sizes (in square feet) of homes and the prices of homes.
> The pulse rates (in beats per minute) and SAT scores of adults
> The weights of gasoline-powered cars and the distances they can travel on a gallon of gas (measured in miles per gallon)
> The distances of taxi cab rides and the costs of trips.
> Golf scores and prize money won by professional golfers (lower scores are better)
> The IQ scores and hat sizes of randomly selected adults.
> Assuming that we want to use the data in the table below to test for independence between wearing a helmet and receiving facial injuries in a bicycle accident, find the expected frequency for the cell with an observed frequency of 83.
> The weights of taxi cab passengers and the costs of trips.
> The total weight of a package you wish to mail and the cost to mail it
> The two variables I studied showed such a strong correlation that they had a correlation coefficient of r = 1.50.
> The scatter plot showed all the data points following a nearly straight diagonal line, but only a weak correlation between the two variables being plotted.
> Numerous studies have found a negative correlation between the amount of time a student spends on social media and the student’s GPA, suggesting that if you want a higher GPA, you should spend less time on social media.
> A physician finds that increasing the time spent exercising each week results in a lower resting pulse rate. Because this is a positive result, we say that there is a positive correlation.
> What does the correlation coefficient, r, tell us about the strength of a correlation? What range of values can r have?
> Let A be the event of rolling an odd number on a six-sided dice. Then event not A will be rolling an even number. Are events A and not A overlapping? Why or why not?
> A pollster randomly selects an adult for a survey. Let M denote the event of getting a male, and let R denote the event of getting a Republican. Are events M and R overlapping?

