Question: The forecaster in Exercise 15.2 augments
The forecaster in Exercise 15.2 augments her AR (4) model for IP growth to include four lagged values of ∆Rt, where Rt is the interest rate on three-month U.S. Treasury bills (measured in percentage points at an annual rate).
a. The F-statistic on the four lags of ∆Rt is 3.91. Do interest rates help predict IP growth? Explain.
b. The researcher also regresses ∆Rt on a constant, four lags of ∆Rt, and four lags of IP growth. The resulting F-statistic on the four lags of IP growth is 1.48. Does IP growth help to predict interest rates? Explain.
Data from Exercise 15.2:
The Index of Industrial Production (IPt) is a monthly time series that measures the quantity of industrial commodities produced in a given month. This problem uses data on this index for the United States. All regressions are estimated over the sample period 1986:M1–2017:M12 (that is, January 1986 through December 2017). Let Yt = 1200 * ln (IPt > IPt - 1).
a. A forecaster states that Yt shows the monthly percentage change in IP, measured in percentage points per annum. Is this correct? Why?
b. Suppose she estimates the following AR (4) model for Yt:
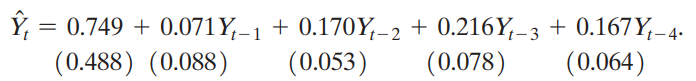
Use this AR (4) to forecast the value of Yt in January 2018, using the following values of IP for July 2017 through December 2017:

c. Worried about potential seasonal fluctuations in production, she adds Yt-12 to the autoregression. The estimated coefficient on Yt-12 is −0.061, with a standard error of 0.043. Is this coefficient statistically significant?
d. Worried about a potential break, she computes a QLR test (with 15% trimming) on the constant and AR coefficients in the AR (4) model. The resulting QLR statistic is 1.80. Is there evidence of a break? Explain.
e. Worried that she might have included too few or too many lags in the model, the forecaster estimates AR(p) models for p = 0, 1, ……, 6 over the same sample period. The sum of squared residuals from each of these estimated models is shown in the table. Use the BIC to estimate the number of lags that should be included in the autoregression. Do the results differ if you use the AIC?

> Consider the population regression of test scores against income and the square of income in Equation (8.1). a. Write the regression in Equation (8.1) in the matrix form of Equation (19.5). Define Y, X, U, and B. b. Explain how to test the null hypothesi
> Prove Equation (18.16) under assumptions 1 and 2 of Key Concept 18.1 plus the assumption that Xi and ui have eight moments. Data from Equation 18.16:
> Consider the regression model in Key Concept 18.1, and suppose that assumptions 1, 2, 3, and 5 hold. Suppose that assumption 4 is replaced by the assumption that var (ui | Xi) = θ0 + θ1 |Xi|, where |Xi| is the absolute value of Xi, θ0 > 0, and θ1 >= 0.
> This exercise provides an example of a pair of random variables, X and Y, for which the conditional mean of Y given X depends on X but corr (X, Y) = 0. Let X and Z be two independently distributed standard normal random variables, and let Y = X2 + Z. a.
> Suppose that X and u are continuous random variables and (Xi, ui), i = 1… n, are i.i.d. a. Show that the joint probability density function (p.d.f.) of (ui, uj, Xi, Xj) can be written as f(ui , Xi) f(uj , Xj) for i ≠ j, where f(ui , Xi) is the joint p.d.
> Show that if ^1 is conditionally unbiased, then it is unbiased; that is, show that if E (^1 X1, Xn) = 1, then E (^1) = 1.
> Suppose that W is a random variable with E (W4) < ∞. Show that E (W2) < ∞.
> Show the following results: a. Show that Where a2 is a constant, implies that ^1 is consistent. b. Show that Implies that
> This exercise fills in the details of the derivation of the asymptotic distribution of b^1 given in Appendix 4.3. a. Use Equation (18.19) to derive the expression Where vi = (Xi - mX) ui. b. Use the central limit theorem, the law of large numbers, and Sl
> Suppose that (Xi, Yi) are i.i.d. with finite fourth moments. Prove that the sample covariance is a consistent estimator of the population covariance—that is, that Where sXY is defined in Equation (3.24). Data from Equation 3.24:
> Z is distributed N (0, 1), W is distributed x2n, and V is distributed x2m. Show, as n --- ∞ and m is fixed, that a. b. Use the result to explain why the t ∞ distribution is the same as the standard normal distribution.
> Suppose that Yi, i = 1, 2 … n, are i.i.d. with E (Yi) = m, var (Yi) = 2, and finite fourth moments. Show the following:
> Consider the heterogeneous regression model Yi = b0i + b1i Xi + ui, where b0i and b1i are random variables that differ from one observation to the next. Suppose that E (ui | Xi) = 0 and (0i, 1i) are distributed indepen
> a. Suppose that u∼N (0, 2u). Show that E (eu) = e1/22u. b. Suppose that the conditional distribution of u given X = x is N (0, a + bx2), where a, and b are positive constants. Show that E (eu | X = x) = e 1/2(a + bx2).
> Suppose you have some money to invest, for simplicity $1, and you are planning to put a fraction w into a stock market mutual fund and the rest, 1 - w, into a mutual fund. Suppose that $1 invested in a stock fund yields Rs after one year and that $1 inve
> Suppose that X and Y are distributed bivariate normal with the density given in Equation (18.38). a. Show that the density of Y given X = x can be written as Where b. Use the result in (a) to show that c. Use the result in (b) to show that E(YX = x) = a
> Let θ^ be an estimator of the parameter θ, where θ^ might be biased. Show that if Then
> Consider the regression model without an intercept term, Yi = b1Xi + ui (so the true value of the intercept, b0, is 0). a. Derive the least squares estimator of b1 for the restricted regression model Yi = b1Xi + ui. This is called the restricted least sq
> a. Suppose that E (ut | ut - 1, ut – 2 …) = 0, that var (ut ut - 1, ut - 2, …) follows the ARCH (1) model 2t = a0 + a1u2t - 1, and that the process for ut is stationary. Show th
> Consider the following two-variable VAR model with one lag and no intercept: a. Show that the iterated two-period ahead forecast for Y can be written as And derive values for 1 and 2 in terms of the coefficients in
> Suppose that ∆Yt = ut, where ut is i.i.d. N (0, 1), and consider the regression Yt = bXt + error, where Xt = ∆Yt + 1 and error is the regression error. Show that
> A regression of Yt onto current, past, and future values of Xt yields a. Rearrange the regression so that it has the form shown in Equation (17.25). What are the values of u, -1, 0, and 1? i. Su
> Verify Equation (17.20). Data from Equation 17.20:
> Suppose that Yt follows the AR (p) model Yt = 0 + 1Yt - 1 + g+ bpYt - p + ut, where E (ut Yt - 1, Yt - 2 …) = 0. Let Yt + h t = E (Yt + h Yt, Yt - 1,). Show that Yt + h| t = 0 + 1Yt - 1 + h| t + … + pYt - p + h t for h > p.
> Suppose that E (ut |ut - 1, ut - 2 . . .) = 0 and ut follows the ARCH process, 2t = 1.0 + 0.5 u2t - 1. a. Let E (u2t) = var (ut) be the unconditional variance of ut. Show that var (ut) = 2. (Hint: Use the law of iterated expectations, E (u2t) = E [Eu2t|
> X is a random variable with moments E(X), E(X2), E(X3), and so forth. a. Show E (X - (3 = E(X3) – 3[E(X2)] [E(X) + 2[E(X)]3 b. Show E (X - (4 = E(X4) – 4[E(X)] [E(X3) + 6[E(X)]2 [E(X2) – 3[E(X)] 4
> One version of the expectations theory of the term structure of interest rates holds that a long-term rate equals the average of the expected values of shortterm interest rates into the future plus a term premium that is I (0). Specifically, let Rkt deno
> Consider the cointegrated model YT = uXt + v1t and Xt = Xt - 1 + v2t, where v1t and v2t are mean 0 serially uncorrelated random variables with E (v1t v2j) = 0 for all t and j. Derive the vector error correction model for X and Y.
> Suppose that Yt follows a stationary AR (1) model, Yt = b0 + b1Yt - 1 + ut. a. Show that the h-period ahead forecast of Yt is given by b. Suppose that Xt is related to Yt by Show that
> Consider the constant-term-only regression model Yt = 0 + ut, where ut follows the stationary AR (1) model ut = 1ut - 1 + u∼t with u∼t i.i.d. with mean 0and variance ï
> Consider the model in Exercise 16.7 with Xt = u∼t + 1. a. Is the OLS estimator of 1 consistent? Explain. b. Explain why the GLS estimator of 1 is not consistent. c. Show that the infeasible GLS esti
> Consider the regression model Yt = 0 + 1Xt + ut, where ut follows the stationary AR (1) model ut = 1ut - 1 + u∼t with u∼t i.i.d. with mean 0 and variance 2u and |1| < 1. a. Suppose that Xt is independent of u∼j for all t and j. Is Xt exogenous (past
> Consider the regression model Yt = 0 + 1Xt + ut, where ut follows the stationary AR (1) model ut = 1ut - 1 + u∼t with u∼t i.i.d. with mean 0 and variance &ium
> Derive Equation (16.7) from Equation (16.4), and show that 0 = 0, 1 = 1, 2 = 1 + 2, 3 = ï&c
> Suppose that oil prices are strictly exogenous. Discuss how you could improve on the estimates of the dynamic multipliers in Exercise 16.1. Data from Exercise 16.1: Increases in oil prices have been blamed for several recessions in developed countries.
> Consider two different randomized experiments. In experiment A, oil prices are set randomly, and the central bank reacts according to its usual policy rules in response to economic conditions, including changes in the oil price. In experiment B, oil pric
> Consider three random variables, X, Y, and Z. Suppose that Y takes on k values y1, ……., yk; that X takes on l values x1, ……., xl; and that Z takes on m values z1, â
> Use the probability distribution given in Table 2.2 to compute (a) E(Y) and E(X); (b) 2X and 2Y; and (c) XY and corr (X, Y). Data from Table 2.2:
> Macroeconomists have also noticed that interest rates change following oil price jumps. Let Rt denote the interest rate on three-month Treasury bills (in percentage points at an annual rate). The distributed lag regression relating the change in Rt(&acir
> Suppose Yt = 0 + ut, where ut follows a stationary stationary AR (1) ut = 1ut - 1 + u∼t with u∼t i.i.d. with mean 0 and variance 2u and |1
> Suppose that a(L) = (1 - L), with |1| < 1, and b(L) = 1 + L +2L2 +3L3 ……. a. Show that the product b(L)a(L) = 1, so that b(L) = a(L)-1. b. Why is the restriction |1| < 1 important?
> Consider the ADL model Yt = 5.3 + 0.2Yt - 1 + 1.5Xt - 0.1Xt - 1 + u∼t, where Xt is strictly exogenous. a. Derive the impact effect of X on Y. b. Derive the first five dynamic multipliers. c. Derive the first five cumulative multipliers. d. Derive the lon
> Increases in oil prices have been blamed for several recessions in developed countries. To quantify the effect of oil prices on real economic activity, researchers have run regressions like those discussed in this chapter. Let GDPt denote the value of qu
> The moving average model of order q has the form Yt = 0 + et + 1et - 1 + 2et - 2 + ……+ qet - q, where et is a serially uncorrelated random var
> Suppose Yt is the monthly value of the number of new home construction projects started in the United States. Because of the weather, Yt has a pronounced seasonal pattern; for example, housing starts are low in January and high in June. Let Jan denote t
> Suppose Yt follows the stationary AR (1) model Yt = 2.5 + 0.7Yt - 1 + ut, where ut is i.i.d. with E (ut) = 0 and var (ut) = 9. a. Compute the mean and variance of Yt. b. Compute the first two autocovariances of Yt. c. Compute the first two autocorrelatio
> In this exercise, you will conduct a Monte Carlo experiment to study the phenomenon of spurious regression discussed. In a Monte Carlo study, artificial data are generated using a computer, and then those artificial data are used to calculate the statist
> Prove the following results about conditional means, forecasts, and forecast errors: a. Let W be a random variable with mean W and variance 2w, and let c be a constant. Show that E [(W – c)2] = 2w + (W – c)2. b. Consider the problem of forecasting Yt
> Consider two random variables, X and Y. Suppose that Y takes on k values y1, ……., yk and that X takes on l values x1, ……. ,xl. a. Show that; b. Use your answer to (a) to veri
> Using the same data as in Exercise 15.2, a researcher tests for a stochastic trend in ln (IPt), using the following regression: where the standard errors shown in parentheses are computed using the homoskedasticity-only formula and the regressor t is a l
> The Index of Industrial Production (IPt) is a monthly time series that measures the quantity of industrial commodities produced in a given month. This problem uses data on this index for the United States. All regressions are estimated over the sample pe
> Suppose Yt follows a random walk, Yt = Yt−1 + ut, for t = 1, ……, T, where Y0 = 0 and ut is i.i.d. with mean 0 and variance 2u. a. Compute the mean and variance of Yt. b. Compute the covariance between Yt and Yt−k. c. Use the results in (a) and (b) to sh
> Consider the stationary AR (1) model Yt = b0 + b1Yt−1 + ut, where ut is i.i.d. with mean 0 and variance 2u. The model is estimated using data from time periods t = 1 through t = T, yielding the OLS estimators b^0 and b^1. You are interested in forecasti
> Suppose ∆Yt follows the AR (1) model ∆Yt = 0 +∆Yt - 1 + ut. a. Show that Yt follows an AR (2) model. b. Derive the AR (2) coefficients for Yt as a function of 0 and 1.
> A researcher carries out a QLR test using 30% trimming, and there are q = 5 restrictions. Answer the following questions, using the values in Table 15.5 (“Critical Values of the QLR Statistic with 15% Trimming”) and Ap
> Consider the AR (1) model Yt = 0 + 1Yt - 1 + ut. Suppose the process is stationary. a. Show that E (Yt) = E (Yt – 1). b. Show that E (Yt) = 0 / (1 - 1).
> You have a sample of size n = 1 with data y1 = 2 and x1 = 1. You are interested in the value of in the regression Y = X + u. a. Plot the sum of squared residuals (y1 - bx1)2 as function of b. b. Show that the least squares estimate of b is b^OLS = 2.
> Let X and Y be two random variables. Denote the mean of Y given X = x by (x) and the variance of Y by 2(x). a. Show that the best (minimum MSPE) prediction of Y given X = x is (x) and the resulting MSPE is 2(x). b. Suppose X is chosen at random. Use
> In any year, the weather can inflict storm damage to a home. From year to year, the damage is random. Let Y denote the dollar value of damage in any given year. Suppose that in 95% of the years Y = $0, but in 5% of the years Y = $30,000. a. What are the
> In Exercise 14.5(b), suppose you predict Y using Y - 1 instead of Y. a. Compute the bias of the prediction. b. Compute the mean of the prediction error. c. Compute the variance of the prediction error. d. Compute the MSPE of the prediction. e. Does Y - 1
> In Exercise 14.5(b), suppose you predict Y using Y/2 instead of Y. a. Compute the bias of the prediction. b. Compute the mean of the prediction error. c. Compute the variance of the prediction error. d. Compute the MSPE of the prediction e. Does Y/2 prod
> Y is a random variable with mean = 2 and variance 2 = 25. a. Suppose you know the value of i. What is the best (lowest MSPE) prediction of the value of Y? That is, what is the oracle prediction of Y? ii. What is the MSPE of this prediction? b. Supp
> Describe the relationship, if any, between the standard error of a regression and the square root of the MSPE of the regression’s out-of-sample predictions.
> Consider the fixed-effects panel data model Yjt = j + ujt for j = 1, ……, k and t = 1, ……, T. Assume that ujt is i.i.d. across entities j and over time t wi
> Let X1 and X2 be two positively correlated random variables, both with variance 1. a. (Requires calculus) The first principal component, PC1, is the linear combination of X1 and X2 that maximizes var (w1X1 + w2X2), where Show that b. The second principal
> You have a sample of size n = 1 with data y1 = 2 and x1 = 1. You are interested in the value of in the regression Y = X + u. (Note there is no intercept.) a. Plot the sum of squared residuals (y1 - bxl)2 as function of b. b. Show that the least square
> A researcher is interested in predicting average test scores for elementary schools in Arizona. She collects data on three variables from 200 randomly chosen Arizona elementary schools: average test scores (TestScore) on a standardized test, the fraction
> Derive the final equality in Equation (13.10). (Use the definition of the covariance, and remember that, because the actual treatment Xi is random, b1i and Xi are independently distributed.) Data from Equation 13.10:
> Suppose you have the same data as in Exercise 13.7 (panel data with two periods, n observations), but ignore the W regressor. Consider the alternative regression model where Gi = 1 if the individual is in the treatment group and Gi = 0 if the individual
> Yi, i = 1, …, n, are i.i.d. Bernoulli random variables with p = 0.6. Let Y denote the sample mean. a. Use the central limit theorem to compute approximations for i. Pr (Y >= 0.64) when n = 50. ii. Pr (Y Y > 0.55) = 0.95? (Use the central limit theorem
> Suppose you have panel data from an experiment with T = 2 periods (so t = 1, 2). Consider the panel data regression model with fixed individual and time effects and individual characteristics Wi that do not change over time. Let the treatment be binary,
> Suppose there are panel data for T = 2 time periods for a randomized controlled experiment, where the first observation (t = 1) is taken before the experiment and the second observation (t = 2) is for the post treatment period. Suppose the treatment is b
> Consider a study to evaluate the effect on college student grades of dorm room Internet connections. In a large dorm, half the rooms are randomly wired for high-speed Internet connections (the treatment group), and final course grades are collected for a
> A new law will increase minimum wages in City A next year but not in City B, a city much like City A. You collect employment data from a random selected sample of restaurants in cities A and B this year, and you plan to return and collect data at restaur
> Suppose that, in a randomized controlled experiment of the effect of an SAT preparatory course on SAT scores, the following results are reported: a. Estimate the average treatment effect on test scores. b. Is there evidence of non-random assignment? Expl
> For the following calculations, use the results in column (3) of Table 13.2. Consider two classrooms, A and B, which have identical values of the regressors in column (3) of Table 13.2, except that: a. Classroom A is a small class, and classroom B is a r
> Consider the potential outcomes framework. Suppose Xi is a binary treatment that is independent of the potential outcomes Yi (1) and Yi (0). Let TEi = Yi (1) – Yi (0) denotes the treatment effect for individual i. a. Can you consistently estimate E [Yi (
> Results of a study by McClelan, McNeill, and Newhouse are reported. They estimate the effect of cardiac catheterization on patient survival times. They instrument the use of cardiac catheterization by the distance between a patient’s home and a hospital
> Consider the regression model with heterogeneous regression coefficients Yi = 0 + 1iXi + vi, where (vi, Xi, 1i) are i.i.d. random variables with 1 = E (1i). a. Show that the model can be written as Yi = 0 + 1Xi + ui, where ui = (1i - 1) Xi + vi.
> How would you calculate the small class treatment effect from the results in Table 13.1? Can you distinguish this treatment effect from the aide treatment effect? How would you have to change the program to correctly estimate both effects? Data from Tab
> Y is distributed N (10, 100) and you want to calculate Pr (Y
> A researcher is interested in the effect of more secure property rights on income across countries. He collects recent data from 60 countries and runs the OLS regression Yi = 0 + 1Xi + ui, where Yi is a country’s GDP per capita and Xi is an index takin
> Consider a product market with a supply function Qsi = 0 + 1Pi + usi, a demand function Qdi = 0 + udi, and a market equilibrium condition Qsi = Qdi, where usi and udi are mutually independent i.i.d. random variables, both with a mean of 0. a. Show tha
> A classmate has developed an IV regression model with one regressor, Xi, and two instruments, Z1i and Z2i. She has a strong theoretical basis as to why corr (Z1i, ui) = 0, namely that Z1i is the result of a random lottery. Preliminary work, however, show
> Suppose a researcher is considering developing an IV regression model with one regressor, Xi, and one instrument, Zi. If she has a sample of n = 113, what range must the correlation coefficient be between Xi and Zi in order for Zi to be considered a stro
> Consider the IV regression model Yi = 0 + 1Xi + 2Wi + ui, where Xi is correlated with ui and Zi is an instrument. Suppose that the first three assumptions in key concept are satisfied. Which IV assumption is not satisfied when a. Zi is independent of
> Consider TSLS estimation of the effect of a single included endogenous variable, Xi, on Yi using one binary instrument, Zi, which takes values of either 0 or 1. Noting that show that the Wald estimator can be derived from the TSLS estimator in this circu
> A classmate is interested in estimating the variance of the error term in Equation (12.1). a. Suppose she uses the estimator from the second-stage regression of where X^i is the fitted value from the first-stage regression. Is this estimator consistent?
> Consider the regression model with a single regressor: Yi = 0 + 1Xi + ui. Suppose the least squares assumptions in Key Concept 4.3 are satisfied. a. Show that Xi is a valid instrument. That is, show that Zi = Xi. b. Show that the IV regression assumpti
> Two classmates are comparing their answers to an assignment. One classmate has specified an instrumental variable regression model Yi = 0 + 1Xi + 2Wi + ui, using Zi as an instrument. The other student has specified the same model, but has omitted Wi.
> This question refers to the panel data IV regressions summarized in Table. a. Suppose the federal government is considering a new tax on cigarettes that is estimated to increase the retail price by $0.25 per pack. If the current price per pack is $6.75,
> Suppose Yi, I = 1, 2, …, n is i.i.d. random variables, each distributed N (20, 4). a. Compute Pr (19.6
> Use the estimated linear probability model shown in column (1) of Table 11.2 to answer the following: a. Two applicants, one self-employed and one in salaried employment, apply for a mortgage. They have the same values for all the regressors other than e
> Consider the linear probability model Yi = 0 + 1Xi + ui, and assume that E (ui | Xi) = 0. a. Show that Pr (Yi = 1 | Xi) = 0 + 1Xi. b. Show that var (ui | Xi) = (0 + 1Xi) [1 – (0 + 1Xi)]. c. Is ui heteroskedastic? Explain. d. Derive the likelih
> Repeat Exercise 11.6 using the logit model in Equation (11.10). Are the logit and probit results similar? Explain. Data from Equation 11.10: Data from Exercise 11.6: Use the estimated probit model in Equation (11.8) to answer the following questions: a
> Use the estimated probit model in Equation (11.8) to answer the following questions: a. A black mortgage applicant has a P/I ratio of 0.35. What is the probability that his application will be denied? b. Suppose the applicant reduced this ratio to 0.30.
> Seven hundred income-earning individuals from a district were randomly selected and asked whether they are government employees (Govi = 1) or not (Govi = 0); data were also collected on their gender (Malei = 1 if male and = 0 if female) and their years o
> Seven hundred income-earning individuals from a district were randomly selected and asked whether they are government employees (Govi = 1) or not (Govi = 0); data were also collected on their gender (Malei = 1 if male and = 0 if female) and their years o
> Seven hundred income-earning individuals from a district were randomly selected and asked whether they are government employees (Govi = 1) or not (Govi = 0); data were also collected on their gender (Malei = 1 if male and = 0 if female) and their years o
> Seven hundred income-earning individuals from a district were randomly selected and asked whether they are government employees (Govi = 1) or not (Govi = 0); data were also collected on their gender (Malei = 1 if male and = 0 if female) and their years o

