Question: The graph of the function f (x) = √(
The graph of the function f (x) = √(1 - x2) on the interval -1 ≤ x ≤ 1 is a semicircle. The area under the graph is 1/2 π(1)2 = π/2 = 1.57080, to five decimal places. Use a Riemann sum with n = 5 and midpoints to estimate the area under the graph. See Fig. 15. Carry out the calculations to five decimal places and compute the error (the difference between the estimate and 1.57080).
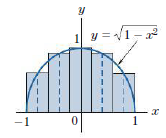
Riemann sum:
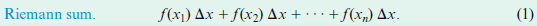
Figure 15:
Transcribed Image Text:
Ricmann sum. f(x1) Δx + f(x2) Δx + +f(x) Δ.χ. (1) -1 y 0 y = √√1 = x² 1
> Let M(x) be a company’s marginal cost at production level x. Give an economic interpretation of the number 0∫100 M(x)dx.
> Let M(x) be a company’s marginal profit at production level x. Give an economic interpretation of the number 44∫48 M(x)dx.
> Suppose that the marginal profit function for a company is P (x) = 100 + 50x - 3x2 at production level x. (a) Find the extra profit earned from the sale of 3 additional units if 5 units are currently being produced. (b) Describe the answer to part (a) as
> Suppose that the marginal cost function of a handbag manufacturer is C (x) = 3/32 x2 - x + 200 dollars per unit at production level x (where x is measured in units of 100 handbags). (a) Find the total cost of producing 6 additional units if 2 units are c
> After t hours of operation, an assembly line is producing lawn mowers at the rate of r(t) = 21 – 4/5 t mowers per hour. (a) How many mowers are produced during the time from t = 2 to t = 5 hours? (b) Represent the answer to part (a) as an area.
> A helicopter is rising straight up in the air. Its velocity at time t is υ(t) = 2t + 1 feet per second. (a) How high does the helicopter rise during the first 5 seconds? (b) Represent the answer to part (a) as an area.
> Find the area of the region bounded by y = 1/x, y = 4x, and y = x/2, for x ≥ 0. (The region resembles the shaded region in Exercise 29.) Figure 27: Y /y = 8x y y=x x
> Find the area in Fig. 27 of the region bounded by y = 1/x2, y = x, and y = 8x, for x ≥ 0. Figure 27: Y /y = 8x y y=x x
> Determine the following: ∫3e-2x dx
> Find the area of the region between y = x2 and y = 1/x2 (a) from x = 1 to x = 4, (b) from x = 1/2 to x = 4.
> Find the area of the region between y = x2 - 3x and the x-axis (a) from x = 0 to x = 3, (b) from x = 0 to x = 4, (c) from x = -2 to x = 3.
> Find the area of the region bounded by the curves. y = 4/x and y = 5 - x
> Find the area of the region bounded by the curves. y = 8x2 and y = √x
> Find the area of the region bounded by the curves. y = x3 and y = 2x2
> Find the area of the region bounded by the curves. y = x(x2 - 1) and the x-axis
> Find the area of the region bounded by the curves. y = x2 - 1 and y = 3
> Find the area of the region bounded by the curves. y = -x2 + 6x - 5 and y = 2x - 5
> Find the area of the region bounded by the curves. y = 4x(1 - x) and y = 3/4
> Find the area of the region bounded by the curves. y = x2 and y = x
> Determine the following: ∫ (7/2x3 – 3√x) dx
> Find the area of the region between the curves. y = e2x and y = 1 - x from x = 0 to x = 1
> Find the area of the region between the curves. y = ex and y = 1/x2 from x = 1 to x = 2
> Find the area of the region between the curves. y = x(2 - x) and y = 2 from x = 0 to x = 2
> Find the area of the region between the curves. y = x2 - 6x + 12 and y = 1 from x = 0 to x = 4
> Find the area of the region between the curves. y = x2 + 1 and y = -x2 - 1 from x = -1 to x = 1
> Find the area of the region between the curves. y = 2x2 and y = 8 (a horizontal line) from x = -2 to x = 2
> Find the area of the region between the curve and the x-axis. f (x) = e-x + 2 from -1 to 2
> Find the area of the region between the curve and the x-axis. f (x) = ex - 3 from 0 to ln 3
> Find the area of the region between the curve and the x-axis. f (x) = x2 + 6x + 5 from 0 to 1.
> Find the area of the region between the curve and the x-axis. f (x) = x2 - 2x - 3, from 0 to 2.
> Determine the following: ∫ (x - 2x2 + 1/3x) dx
> Find the area of the region between the curve and the x-axis. f (x) = x(x2 - 1), from -1 to 1.
> Find the area of the region between the curve and the x-axis. f (x) = 1 - x2, from -2 to 2
> Let g(x) be the function pictured in Fig. 26. Determine whether 1 > 0 g(x)dx is positive, negative, or zero. Figure 26: 2 1 -2 -3 y y = g(x) +x + 1 2 3 4 5/6 7 8
> Let f (x) be the function pictured in Fig. 25. Determine whether 1 > 0 f (x)dx is positive, negative, or zero. Figure 25: 3 2 1 -1 Y 12 y = f(x) 3 4 5 7 8 8
> Shade the portion of Fig. 24 whose area is given by the integral 0∫1L [ f (x) - g (x)] + 1∫2 [ g (x) - f (x)] dx. Figure 24: 2 y = f(x) 1 y = g(x) 0 У х а 1 2
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. Y f(x) = -x 2- -2 2 0
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. y 1 0 1 (x)=1 1 2 x
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. 2 Y 0 12 f(x) = 2 23 3 4
> Evaluate a Riemann sum to approximate the area under the graph of f (x) on the given interval, with points selected as specified. f (x) = x√(1 + x2); 1 ≤ x ≤ 3, n = 20, midpoints of subintervals f
> Evaluate a Riemann sum to approximate the area under the graph of f (x) on the given interval, with points selected as specified. f (x) = x√(1 + x2); 1 ≤ x ≤ 3, n = 20, midpoints of subintervals
> Determine the following: ∫ (2/√x + 2√x) dx
> Compute the area under the graph of y = 1 / (1 + x2) from 0 to 5.
> The area under the graph of the function e-x2 plays an important role in probability. Compute this area from -1 to 1.
> We show that, as the number of subintervals increases indefinitely, the Riemann sum approximation of the area under the graph of f (x) = x2 from 0 to 1 approaches the value 1/3 , which is the exact value of the area. Partition the interval [0, 1] into n
> We show that, as the number of subintervals increases indefinitely, the Riemann sum approximation of the area under the graph of f (x) = x2 from 0 to 1 approaches the value 1/3 , which is the exact value of the area. Verify the given formula for n = 1, 2
> A farmer wants to divide the lot in Fig. 18 into two lots of equal area by erecting a fence that extends from the road to the river as shown. Determine the location of the fence. Figure 18: 10 20 30 40 Road 50 60 70 80 06 ft 40 ft 35 ft 30 ft 25 ft
> Estimate the area (in square feet) of the residential lot in Fig. 17. Figure 17: 0 20 60 100 140 160 106 ft 101 ft 100 ft 113 ft
> Use a Riemann sum with n = 5 and midpoints to estimate the area under the graph of f (x) = √(1 - x2) on the interval 0 ≤ x ≤ 1. The graph is a quarter circle, and the area under the graph is .7854
> Use a Riemann sum with n = 4 and right endpoints to estimate the area under the graph of f (x) = 2x - 4 on the interval 2 ≤ x ≤ 3. Then, repeat with n = 4 and midpoints. Compare the answers with the exact answer, 1
> Use a Riemann sum with n = 4 and left endpoints to estimate the area under the graph of f (x) = 4 - x on the interval 1 ≤ x ≤ 4. Then repeat with n = 4 and midpoints. Compare the answers with the exact answer, 4.5,
> Determine the following: ∫x√x dx
> Use a Riemann sum to approximate the area under the graph of f (x) in Fig. 14 on the given interval, with selected points as specified. Draw the approximating rectangles. 1 ≤ x ≤ 7, n = 3, midpoints of subintervals
> Use a Riemann sum to approximate the area under the graph of f (x) in Fig. 14 on the given interval, with selected points as specified. Draw the approximating rectangles. 4 ≤ x ≤ 9, n = 5, right endpoints Riemann
> Use a Riemann sum to approximate the area under the graph of f (x) in Fig. 14 on the given interval, with selected points as specified. Draw the approximating rectangles. 3 ≤ x ≤ 7, n = 4, left endpoints Riemann s
> Use a Riemann sum to approximate the area under the graph of f (x) in Fig. 14 on the given interval, with selected points as specified. Draw the approximating rectangles. 0 ≤ x ≤ 8, n = 4, midpoints of subintervals
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = ln x; 2 ≤ x ≤ 4, n = 5, left endpoints Riemann sum: Ricmann sum. f(x1) Δx +
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = e-x; 2 ≤ x ≤ 3, n = 5, right endpoints Riemann sum: Ricmann sum. f(x1) Δx +
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = x3; 0 ≤ x ≤ 1, n = 5, right endpoints Riemann sum: Ricmann sum. f(x1) Δx +
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = x3; 1 ≤ x ≤ 3, n = 5, left endpoints Riemann sum: Ricmann sum. f(x1) Δx + f
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = x2; -2 ≤ x ≤ 2, n = 4, midpoints of subintervals Riemann sum: Ricmann sum.
> Use a Riemann sum to approximate the area under the graph of f (x) on the given interval, with selected points as specified. f (x) = x2; 1 ≤ x ≤ 3, n = 4, midpoints of subintervals Riemann sum: Ricmann sum. f
> Determine the following: ∫1/7x dx
> Determine Δx and the midpoints of the subintervals formed by partitioning the given interval into n subintervals. 3 ≤ x ≤ 5; n = 5
> Determine Δx and the midpoints of the subintervals formed by partitioning the given interval into n subintervals. 1 ≤ x ≤ 4; n = 5
> Determine Δx and the midpoints of the subintervals formed by partitioning the given interval into n subintervals. 0 ≤ x ≤ 3; n = 6
> Determine Δx and the midpoints of the subintervals formed by partitioning the given interval into n subintervals. 0 ≤ x ≤ 2; n = 4
> Find the real number b 7 0 so that the area under the graph of y = x2 from 0 to b is equal to the area under the graph of y = x3 from 0 to b.
> Find the real number b > 0 so that the area under the graph of y = x3 from 0 to b is equal to 4.
> Find the area under each of the given curves. y = e3x; x = - 1/3 to x = 0
> Find the area under each of the given curves. y = (x - 3)4; x = 1 to x = 4
> Find the area under each of the given curves. y = √x; x = 0 to x = 4
> Find the area under each of the given curves. y = 3x2 + x + 2ex/2; x = 0 to x = 1
> Determine the following: ∫ (2/x + x/2) dx
> Find the area under each of the given curves. y = 3x2; x = -1 to x = 1
> Find the area under each of the given curves. y = 4x; x = 2 to x = 3
> Draw the region whose area is given by the definite integral. 0∫4√x dx
> Draw the region whose area is given by the definite integral. 0∫4 (8 - 2x) dx
> Draw the region whose area is given by the definite integral. 2∫4 x2 dx
> Use Theorem I to compute the shaded area in Exercise 11. Shaded area in Exercise 11: Theorem 1: y y = x + 1 1 3 y=x Theorem I: Area under a Graph If f(x) is a continuous nonnegative function on the interval a ≤ x ≤ b, then the area under the grap
> Use Theorem I to compute the shaded area in Exercise 8. Shaded area in Exercise 8: Theorem 1: 0 थ्र y = - 0(0 – 3) 3 Theorem I: Area under a Graph If f(x) is a continuous nonnegative function on the interval a ≤ x ≤ b, then the area under the gra
> Use Theorem I to compute the shaded area in Exercise 7. Shaded Area in Exercise 7: Theorem 1: Y 0 f(x)=1/ 1 2 Theorem I: Area under a Graph If f(x) is a continuous nonnegative function on the interval a ≤ x ≤ b, then the area under the graph of f
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. y 2. 1 0 x+1 I 1 1 3-x 2
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. y y = x + ² 1 3 y=x
> Determine the following: ∫x * x2 dx
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. Y -1 이 y=e 2
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. Y f(x) = ln x 1 2
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. fi 0 y = -x(x-3) 3 x
> Set-up the definite integral that gives the area of the shaded region. Do not evaluate the integral. Y 0 f(x)=1/ 1 2 x
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. 2. g 1 2 3 = 6 - 2x 3 - Ꮖ
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. 1 y 0 y = 1- x 1 y = x - 1 2
> Compute the area of the shaded region in two different ways: (a) by using simple geometric formulas; (b) by applying Theorem I. -2 22 Y 0 f(x) = x + 2 2
> Evaluate the given integral. 1∫4 (3√t + 4t) dt
> Evaluate the given integral. -1∫2(x2/3 – 2/9x) dx
> Evaluate the given integral. 0∫1 (2x – 3/4) dx
> Determine the following: ∫x/c dx (c a constant ≠ 0)
> A conical-shaped tank is being drained. The height of the water level in the tank is decreasing at the rate h (t) = - t/2 inches per minute. Find the decrease in the depth of the water in the tank during the time interval 2 ≤ t ≤ 4.
> A saline solution is being flushed with fresh water in such a way that salt is eliminated at the rate r(t) = -(t + ½) grams per minute. Find the amount of salt that is eliminated during the first 2 minutes.
> A sample of radioactive material with decay constant .1 is decaying at a rate R(t) = -e-0.1t grams per year. How many grams of this material decayed after the first 10 years?
> Using the data from the previous exercise, find P(t). Exercise 40: You took a $200,000 home mortgage at an annual interest rate of 3%. Suppose that the loan is amortized over a period of 30 years, and let P(t) denote the amount of money (in thousands of

