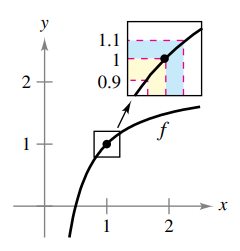
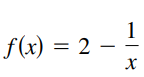Question: The graph of / is shown in the
> Prove that if the limit of f(x) as x approaches c exists, then the limit must be unique. [Hint: Let / f(x) = L1 and / f(x) = L2 and prove that L1 = L2.]
> Use a graphing utility to evaluate for several values of n. What do you notice?
> Use a graphing utility to evaluate for several values of n. What do you notice?
> Find the derivative of the function by the limit process. f(x) = x2 − 5
> Consider the function f(x) = √x.
> Consider the function f(x) = √x.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If the limit of f(x) as x approaches c is 0, then there must exist a number k such that f(k) < 0.001.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f is undefined at x = c, then the limit of f(x) as x approaches c does not exist.
> Use the graph of f to identify the values of c for which / f(x) exists. a. / b. /
> The statement means that for each ε > 0 there corresponds a δ > 0 such that if 0 If ε = 0.001, then Use a graphing utility to graph each side of this inequality. Use the zoom feature to find an interval (2 &ac
> Consider the function Estimate by evaluating f at x-values near 0. Sketch the graph of f.
> Consider the function f(x) = (1 + x)1/x Estimate by evaluating f at x-values near 0. Sketch the graph of f.
> Find the derivative of the function by the limit process. f(x) = x2 + x – 3
> A sporting goods manufacturer designs a golf ball having a volume of 2.48 cubic inches. a. What is the radius of the golf ball? b. The volume of the golf ball varies between 2.45 cubic inches and 2.51 cubic inches. How does the radius vary? c. Use the ε-
> A jeweler resizes a ring so that its inner circumference is 6 centimeters. a. What is the radius of the ring? b. The inner circumference of the ring varies between 5.5 centimeters and 6.5 centimeters. How does the radius vary? c. Use the ε-δ definit
> If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain your reasoning.
> If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2? Explain your reasoning.
> The definition of limit requires that f is a function defined on an open interval containing c, except possibly at c. Why is this requirement necessary?
> When using the definition of limit to prove that L is the limit of f(x) as x approaches c, you find the largest satisfactory value of δ. Why would any smaller positive value of δ also work?
> For a long-distance phone call, a hotel charges $5.79 for the first minute and $0.99 for each additional minute or fraction thereof. A formula for the cost is given by C(t) = 5.79 − 0.99[1 – t], t > 0 where t is the time in minutes. (Note: [x] = greatest
> For a long-distance phone call, a hotel charges $9.99 for the first minute and $0.79 for each additional minute or fraction thereof. A formula for the cost is given by C(t) = 9.99 − 0.79⟨1 − t⟩, t > 0 where t is the time in minutes. (Note: [x] = greatest
> Use a graphing utility to graph the function and estimate the limit (if it exists). What is the domain of the function? Can you detect a possible error in determining the domain of a function solely by analyzing the graph generated by a graphing utility?
> Use a graphing utility to graph the function and estimate the limit (if it exists). What is the domain of the function? Can you detect a possible error in determining the domain of a function solely by analyzing the graph generated by a graphing utility?
> Find the derivative of the function by the limit process. f(x) = 5 – 2/3 x
> What is the limit of g(x) = x as x approaches π?
> What is the limit of f(x) = 4 as x approaches π?
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the derivative of the function by the limit process. h(s) = 3 + 2/3s
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Find the limit L. Then find δ such that │f(x) − L│
> Find the limit L. Then find δ such that │f(x) − L│
> Find the limit L. Then find δ such that │f(x) − L│
> Find the limit L. Then find δ such that │f(x) − L│
> Find the limit L. Then find δ such that │f(x) − L│
> Find the limit L. Then find δ such that │f(x) − L│ < ε whenever 0 < │x − c│ < δ for (a) ε = 0.01 and ε = 0.005.
> Find the derivative of the function by the limit process. f(x) = 7x − 3
> The graph of is shown in the figure. Find δ such that if 0 for ε = 0.05, 0.01, and 0.005. What happens to the value of δ as the value of ε gets smaller?
> The graph of is shown in the figure. Find δ such that if 0
> The graph of f(x) = x + 1 is shown in the figure. Find δ such that if 0
> Sketch a graph of a function f that satisfies the given values. (There are many correct answers.) f(−2) = 0 f(2) = 0
> Sketch a graph of a function f that satisfies the given values. (There are many correct answers.) f(0) is undefined. f(2) = 6
> Sketch the graph of f. Then identify the values of c for which / f(x) exists.
> Sketch the graph of f. Then identify the values of c for which / f(x) exists.
> Use the graph of the function f to decide whether the value of the given quantity exists. If it does, find it. If not, explain why. a. f(-2) b. / c. f(0) d. / e. f(2) f. / g. f(4) h. /
> Use the graph of the function f to decide whether the value of the given quantity exists. If it does, find it. If not, explain why. a. f(1) b. / c. f(4) d. /
> Find the derivative of the function by the limit process. f(x) = −5x
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Use the graph to find the limit (if it exists). If the limit does not exist, explain why.
> Create a table of values for the function and use the result to explain why the limit does not exist.
> Create a table of values for the function and use the result to explain why the limit does not exist.
> Find the derivative of the function by the limit process. g(x) = −3
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Create a table of values for the function and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Find the derivative of the function by the limit process. f(x) = 7
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Complete the table and use the result to estimate the limit. Use a graphing utility to graph the function to confirm your result.
> Is the limit of f(x) as x approaches c always equal to f(c)? Why or why not?
> Given the limit use a sketch to show the meaning of the phrase “0
> Identify three types of behavior associated with the nonexistence of a limit. Illustrate each type with a graph of a function.
> Write a brief description of the meaning of the notation
> Consider the length of the graph of f(x) = 5/x from (1, 5) to (5, 1).
> How would you describe the instantaneous rate of change of an automobile’s position on a highway?
> Find the slope of the tangent line to the graph of the function at the given point. h(t) = t2 + 4t, (1, 5)
> Estimate the slope of the graph at the points (x1, y1) and (x2, y2).
> How does the tax benefit rule apply in the following cases? a. In 2019, the Orange Furniture Store, an accrual method sole proprietorship, sold furniture on credit for $1,000 to Sammy. The cost of the furniture was $600. In 2020, Orange took a bad debt d
> Sanjay receives a settlement letter from the IRS after his discussion with an IRS appeals officer. He is not satisfied with the $101,000 settlement offer. Identify the relevant issues facing Sanjay if he chooses to contest the settlement offer.
> Starting in 2010 Chuck and Luane have been purchasing Series EE bonds in their name to use for the higher education of their daughter Susie, who currently is age 18. During the year, they cash in $12,000 of the bonds to use for freshman year tuition, fee
> Tonya, who lives in California, inherited a $100,000 State of California bond in 2021. Her marginal Federal tax rate is 35%, she itemizes deductions on her Federal tax return, and her marginal state tax rate is 5%. The California bond pays 3.3% interest,
> In January 2021, Ezra purchased 2,000 shares of Gold Utility Mutual Fund for $20,000. In June, Ezra received an additional 100 shares as a dividend, in lieu of receiving $1,000 in cash dividends. In December, the company declared a two-for-one stock spli
> On March 15, 2021, Helen purchased and placed in service a new Escalade. The purchase price was $62,000, and the vehicle had a rating of 6,500 GVW. The vehicle was used 100% for business. a. Assuming that Helen does not use additional first-year deprecia
> George is a U.S. citizen who is employed by Hawk Enterprises, a global company. Beginning on June 1, 2021, George began working in London. He worked there until January 31, 2022, when he transferred to Paris. He worked in Paris the remainder of 2022. His
> On October 15, 2021, Jon purchased and placed in service a used car. The purchase price was $38,000. This was the only business use asset Jon acquired in 2021. He used the car 80% of the time for business and 20% for personal use. Jon used the regular MA