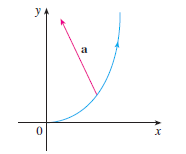
Question: The magnitude of the acceleration vector a

> Find the limit, if it exists, or show that the limit does not exist. 5y cos?x lim (x, y)(0, 0) x + y* 4

> Find the limit, if it exists, or show that the limit does not exist. x* – 4y? lim (x, y (0, 0) x? + 2y?

> Find the limit, if it exists, or show that the limit does not exist. lim (x, y)- (3, 2) evzi-y

> Find the limit, if it exists, or show that the limit does not exist. lim (x, y)- (m, w/2) y sin(x – y)

> Use a table of numerical values of f (x, y) for (x, y) near the origin to make a conjecture about the value of the limit of f (x, y) as (x, y) → (0, 0). Then explain why your guess is correct. 2ху f(x, y) = x² + 2y²

> Use a table of numerical values of f (x, y) for (x, y) near the origin to make a conjecture about the value of the limit of f (x, y) as (x, y) → (0, 0). Then explain why your guess is correct. x*y* + x*y* ² – 5 2 f(x, y) = 2 - xy

> Explain why each function is continuous or discontinuous. (a). The outdoor temperature as a function of longitude, latitude, and time (b). Elevation (height above sea level) as a function of longitude, latitude, and time (c). The cost of a taxi ride as a

> Suppose that lim (x, y) → (3, 1) f (x, y) = 6. What can you say about the value of f (3, 1)? What if f is continuous?

> Graph the functions In general, if t is a function of one variable, how is the graph of obtained from the graph of t? f(x, y) = /x² + y² f(x, y) = evya f(x, y) = Inx? + y2 f(x, y) = sin(/r? + y² 1 f(x, y) x² + y? f(x, y) = 9(Vx² + y?)

> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = t i + 2 cos t j + sin t k, t = 0

> Use a computer to investigate the family of surfaces z = x2 + y2 + cxy. In particular, you should determine the transitional values of c for which the surface changes from one type of quadric surface to another.

> Use a computer to investigate the family of surfaces z = (ax2 + by2) e-x2-y2 How does the shape of the graph depend on the numbers a and b?

> Investigate the family of functions f (x, y) = ecx2+y2. How does the shape of the graph depend on c?

> Graph the function using various domains and viewpoints. Comment on the limiting behavior of the function. What happens as both x and y become large? What happens as (x, y) approaches the origin? f(x, y) x? + y?

> Graph the function using various domains and viewpoints. Comment on the limiting behavior of the function. What happens as both x and y become large? What happens as (x, y) approaches the origin? x + y f(x, y) = x? + y?

> Use a computer to graph the function using various domains and viewpoints. Get a printout that gives a good view of the “peaks and valleys.” Would you say the function has a maximum value? Can you identify any points on the graph that you might consider

> Use a computer to graph the function using various domains and viewpoints. Get a printout that gives a good view of the “peaks and valleys.” Would you say the function has a maximum value? Can you identify any points on the graph that you might consider

> Describe how the graph of g is obtained from the graph of f. (a). t (x, y) = f (x - 2, y) (b). t (x, y) = f (x, y + 2) (c). t (x, y) = f (x + 3, y – 4)

> Describe how the graph of g is obtained from the graph of f . (a). t (x, y) = f (x, y) + 2 (b). t (x, y) = 2f (x, y) (c). t (x, y) = -f (x, y) (d). t (x, y) = 2 - f (x, y)

> Describe the level surfaces of the function. f (x, y, z) = x2 - y2 - z2

> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = t i + t2 j + 2 k, t = 1

> If c ∈ Vn, show that the function f given by f (x) = c ∙ x is continuous on Rn.

> Show that the function f given by f (x) = |x | is continuous on Rn. [Hint: Consider |x - a |2 = (x – a) ∙ (x – a).]

> Let (a). Show that f (x, y) → 0 as (x, y) → (0, 0) along any path through s0, 0d of the form y = mxu with 0 (b). Despite part (a), show that f is discontinuous at (0, 0). (c). Show that f is discontinuous on two enti

> Graph and discuss the continuity of the function sin xy if ху # 0 f(x, y) = ху 1 if xy = 0

> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = (1 - x2) (1 - y2) B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O

> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = sin x - sin y B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O OD

> Determine the set of points at which the function is continuous. ху if (x, y) # (0, 0) 2 f(x, y) = if (x, y) = (0, 0)

> Determine the set of points at which the function is continuous. x²y³ f(x, y) = { ² 2.x² + if (x, y) + (0, 0) 1 if (x, y) = (0, 0)

> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = sin(xy) B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O OD O

> Determine the set of points at which the function is continuous. f (x, y, z) = arcsin (x2 + y2 + z2)

> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = et i + e2t j, t = 0

> Determine the set of points at which the function is continuous. G (x, y) = ln (1 + x – y)

> Determine the set of points at which the function is continuous. e* + e H(x, y) = eу — 1

> Use a computer to graph the function using various domains and viewpoints. Get a printout of one that, in your opinion, gives a good view. If your software also produces level curves, then plot some contour lines of the same function and compare with the

> Graph the function and observe where it is discontinuous. Then use the formula to explain what you have observed. 1 f(x, y) = 1 – x² – y? ,2

> Graph the function and observe where it is discontinuous. Then use the formula to explain what you have observed. f (x, y) = e1/(x-y)

> Sketch both a contour map and a graph of the function and compare them. f(x, y) = V36 – 9x² – 4y²

> Sketch both a contour map and a graph of the function and compare them. f (x, y) = x2 + 9y2

> Find h (x, y) = g (f (x, y)) and the set of points at which h is continuous. g(t) = t + In t, f(x, y) : 1 - ху 1+ x?y? .2,2

> Use a computer graph of the function to explain why the limit does not exist. хуз lim (x, y)(0, 0) x? + y6

> Find the limit, if it exists, or show that the limit does not exist. xy4 lim (x, y)- (0, 0) x + y® ,2 8

> The temperature-humidity index I (or humidex, for short) is the perceived air temperature when the actual temperature is T and the relative humidity is h, so we can write I = f (T, h). The following table of values of I is an excerpt from a table compile

> The wave heights h in the open sea depend on the speed v of the wind and the length of time t that the wind has been blowing at that speed. Values of the function h = f (v, t) are recorded in feet in Table 4. Table 4: (a). What is the value of f (40,

> Two contour maps are shown. One is for a function f whose graph is a cone. The other is for a function t whose graph is a paraboloid. Which is which, and why?

> Level curves (isothermals) are shown for the typical water temperature (in 0C) in Long Lake (Minnesota) as a function of depth and time of year. Estimate the temperature in the lake on June 9 (day 160) at a depth of 10 m and on June 29 (day 180) at a dep

> Shown is a contour map of atmospheric pressure in North America on August 12, 2008. On the level curves (called isobars) the pressure is indicated in millibars (mb). (a). Estimate the pressure at C (Chicago), N (Nashville), S (San Francisco), and V (Va

> The position function of a spaceship is and the coordinates of a space station are (6, 4, 9). The captain wants the spaceship to coast into the space station. When should the engines be turned off? 4 r(t) = (3 + f)i + (2 + In f) j + (7- k t2 + 1,

> A contour map for a function f is shown. Use it to estimate the values of f (-3, 3) and f (3, -2). What can you say about the shape of the graph? 70 60 50 40 -1 30 20 10

> Sketch the graph of the function. f (x, y) = x2

> The body mass index is defined in Exercise 39. Draw the level curve of this function corresponding to someone who is 200 cm tall and weighs 80 kg. Find the weights and heights of two other people with that same level curve. Exercise 39: The body mass i

> In Example 2 we considered the function W = f (T, v), where W is the wind-chill index, T is the actual temperature, and v is the wind speed. A numerical representation is given in Table 1 on page 889. Table: (a). What is the value of f (-15, 40)? What

> The body mass index (BMI) of a person is defined by where m is the person’s mass (in kilograms) and h is the height (in meters). Draw the level curves B (m, h) = 18.5, B (m, h) = 25, B (m, h) = 30, and B (m, h) = 40. A rough guideline i

> Find and sketch the domain of the function. f(x, y, 2) = /4 – x² + v9 – y² + VT –

> A manufacturer has modeled its yearly production function P (the monetary value of its entire production in millions of dollars) as a Cobb-Douglas function P (L, K) = 1.47L0.65K0.35 where L is the number of labor hours (in thousands) and K is the inves

> The wind-chill index W discussed in Example 2 has been modeled by the following function: Check to see how closely this model agrees with the values in Table 1 for a few values of T and v. W(T, v) 13.12 + 0.6215T – 11.37v0.16 + 0.3965TV0.16

> What is the connection between vector functions and space curves?

> What is a vector function? How do you find its derivative and its integral?

> If z = 5x2 + y2 and (x, y) changes from (1, 2) to (1.05, 2.1), compare the values of ∆z and dz.

> Find the differential of the function. L = xze-y 2-z2

> Find and sketch the domain of the function. In(2 — х) g(x, y) = 1- x² – y?

> Find the differential of the function. T = 1+ uvw

> Find the differential of the function. m = p5q3.

> Find the differential of the function. u = Jx? + 3y2 %3D

> Find the differential of the function. z = e-2x cos 2πt.

> Verify the linear approximation at (0, 0). ex cos (xy) ≈ x + 1

> Explain why the function is differentiable at the given point. Then find the linearization L(x, y) of the function at that point. f (x, y) = 4 arctan (xy), (1, 1)

> Explain why the function is differentiable at the given point. Then find the linearization L(x, y) of the function at that point. f(x, y) =+Y, 1+ x (1, 3)

> Explain why the function is differentiable at the given point. Then find the linearization L(x, y) of the function at that point. fu, y) — Vху, (1,4)

> (a). If a particle moves along a straight line, what can you say about its acceleration vector? (b). If a particle moves with constant speed along a curve, what can you say about its acceleration vector?

> Explain why the function is differentiable at the given point. Then find the linearization L(x, y) of the function at that point. f (x, y) = 1 + x ln (xy – 5), (2, 3)

> The diffusion equation where D is a positive constant, describes the diffusion of heat through a solid, or the concentration of a pollutant at time t at a distance x from the source of the pollution, or the invasion of alien species into a new habitat.

> If u = e4+4; ,++4,, where af + až + . + a; = 1, show that Fu ax? + = u ax? ax?

> If f and t are twice differentiable functions of a single variable, show that the function u (x, t) = f (x + at) + t (x – at) is a solution of the wave equation given in Exercise 78. Exercise 78: Show that each of the following functions is a solution

> A particle has position function r(t). If r'(t) = c × r(t), where c is a constant vector, describe the path of the particle.

> Find the indicated partial derivative(s). u = x*y*z*; ax dy² az³ .3

> Find the indicated partial derivative(s). a³w aw у+ 22 дг ду дх" дх? ду

> Find the indicated partial derivative(s). V = In(r + s² + t); ar as at

> Find the indicated partial derivative(s). W = Ju + v?; 2 au dv

> Find the indicated partial derivative(s). g (r, s, t) = er sin (st); grst

> Find the indicated partial derivative(s). f (x, y) = x4y2 - x3y; fxxx, fxyx

> Verify that the conclusion of Clairaut’s Theorem holds, that is, uxy = uyx. u = ln (x + 2y)

> Determine the signs of the partial derivatives for the function f whose graph is shown. (a). fx (21, 2) (b). fy (21, 2)

> Verify that the conclusion of Clairaut’s Theorem holds, that is, uxy = uyx. u = x4y3 - y4

> Find all the second partial derivatives. w = V1 + uv? ,2

> Find all the second partial derivatives. v = sin (s2 - t2)

> Find all the second partial derivatives. y 2х + Зу

> Find all the second partial derivatives. f (x, y) = ln (ax + by)

> Determine the signs of the partial derivatives for the function f whose graph is shown. (a). fx (1, 2) (b). fy (1, 2)

> Use the definition of partial derivatives as limits (4) to find fx (x, y) and fy (x, y). f(x, y) = x + y?

> Use the definition of partial derivatives as limits (4) to find fx (x, y) and fy (x, y). f (x, y) = xy2 - x3y

> Find the indicated partial derivative. f (x, y, z) = xyz; fz (e, 1, 0)

> Find the indicated partial derivative. 1- f(x, y, z) = In Vx? + y² + z? 1+ Jx? + y? + z² f,(1, 2, 2)

> Find the indicated partial derivative. f (x, y) = y sin-1 (xy); fy (1, 1 2 )

> Find the indicated partial derivative. R (s, t) = tes/t; Rt (0, 1)

> Find the first partial derivatives of the function. u = sin (x1 + 2x2 + ∙ ∙ ∙ + nxn)

> Find the first partial derivatives of the function. Vx} + x} + .… + x금 u =

> Find the first partial derivatives of the function. ах + By? yz + 8t? Ф(х, у, г, 1) -

> A ball with mass 0.8 kg is thrown southward into the air with a speed of 30 m/s at an angle of 30° to the ground. A west wind applies a steady force of 4 N to the ball in an easterly direction. Where does the ball land and with what speed?

> Find the first partial derivatives of the function. u = xy/z