Question: The marginal cost function C9sxd was defined
The marginal cost function C9sxd was defined to be the derivative of the cost function. The marginal cost of producing x gallons of orange juice is
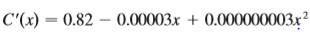
(measured in dollars per gallon). The fixed start-up cost is C(0) = $18,000. Use the Net Change Theorem to find the cost of producing the first 4000 gallons of juice.
Transcribed Image Text:
C'(x) = 0.82 – 0.00003x + 0.000000003x²
> Find the centroid of the region bounded by the given curves. у — 2 — х*, у — х
> A function f is defined by that is, its coefficients are c2n = 1 and c2n+1 = 2 for all n > 0. Find the interval of convergence of the series and find an explicit formula for f(x). f(x) = 1 + 2x + x² + 2x³ + x* + . ||
> Find the centroid of the region bounded by the given curves. y у —х, х— у? x², x=y*
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. y = sin x, y = 0, 0<x<T
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. у —е", у—0, х— 0, х— 1
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. y = Vx, y=0, x= 4 X = 4
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. у — 2х, у— 0, х— 1 y
> The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system. т — 5, т, — 4, тз — 3, т, — 6; P.(-4, 2), Р.0, 5), Р:(3, 2), Р.(1, —2)
> The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system. т, — 4, тз — 2, тз — 4; P (2, — 3), Р.(-3, 1), P:(3, 5)
> The function A defined by is called an Airy function after the English mathematician and astronomer Sir George Airy (1801–1892). (a) Find the domain of the Airy function. (b) Graph the first several partial sums on a common screen. (c)
> A metal plate was found submerged vertically in seawater, which has density 64 lb/ft3. Measurements of the width of the plate were taken at the indicated depths. Use Simpson’s Rule to estimate the force of the water against the plate.
> A swimming pool is 20 ft wide and 40 ft long and its bottom is an inclined plane, the shallow end having a depth of 3 ft and the deep end, 9 ft. If the pool is full of water, find the hydro static force on (a) the shallow end, (b) the deep end, (c) one o
> A dam is inclined at an angle of 30° from the vertical and has the shape of an isosceles trapezoid 100 ft wide at the top and 50 ft wide at the bottom and with a slant height of 70 ft. Find the hydrostatic force on the dam when it is full of water.
> A cube with 20-cm-long sides is sitting on the bottom of an aquarium in which the water is one meter deep. Find the hydrostatic force on (a) the top of the cube and (b) one of the sides of the cube.
> A vertical dam has a semicircular gate as shown in the figure. Find the hydrostatic force against the gate. ]} 2 m `water level 12 m 4 m
> A trough is filled with a liquid of density 840 kg/m3. The ends of the trough are equilateral triangles with sides 8 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough.
> A milk truck carries milk with density 64.6 lb/ft3 in a horizontal cylindrical tank with diameter 6 ft. (a) Find the force exerted by the milk on one end of the tank when the tank is full. (b) What if the tank is half full?
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 2а h
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. a a
> The function J1 defined by is called the Bessel function of order 1. (a) Find its domain. (b) Graph the first several partial sums on a common screen. (c) If your CAS has built-in Bessel functions, graph J1 on the same screen as the partial sums in part
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 ft
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. -2 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 1 4
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 2 ft
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 3 ft
> A tank is 8 m long, 4 m wide, 2 m high, and contains kerosene with density 820 kg/m3 to a depth of 1.5 m. Find (a) the hydrostatic pressure on the bottom of the tank, (b) the hydrostatic force on the bottom, and (c) the hydrostatic force on one end of th
> An aquarium 5 ft long, 2 ft wide, and 3 ft deep is full of water. Find (a) the hydrostatic pressure on the bottom of the aquarium, (b) the hydrostatic force on the bottom, and (c) the hydrostatic force on one end of the aquarium.
> The graph of the concentration function c(t) is shown after a 7-mg injection of dye into a heart. Use Simpson’s Rule to estimate the cardiac output. (mg/L) 4 0 2 4 6 8 10 12 14 í(seconds) 2.
> After a 5.5-mg injection of dye, the readings of dye concentration, in mg/L, at two-second intervals are as shown in the table. Use Simpson’s Rule to estimate the cardiac output. t c(t) t c(1) 0.0 10 4.3 2 4.1 12 2.5 4 8.9 14 1.2 8
> The dye dilution method is used to measure cardiac output with 6 mg of dye. The dye concentrations, in mg/L, are modeled by / where t is measured in seconds. Find the cardiac output.
> High blood pressure results from constriction of the arteries. To maintain a normal flow rate (flux), the heart has to pump harder, thus increasing the blood pressure. Use Poiseuille’s Law to show that if R0 and P0 are normal values of
> A hot, wet summer is causing a mosquito population explosion in a lake resort area. The number of mosquitoes is increasing at an estimated rate of 2200 + 10e0.8t per week (where t is measured in weeks). By how much does the mosquito population increase b
> Pareto’s Law of Income states that the number of people with incomes between / where A and k are constants with A > 0 and k > 1. The average income of these people is Calculate x. x - a and x = b is N – L Ax * dx, ·
> The present value of an income stream is the amount that would need to be invested now to match the future value as described in Exercise 15 and is given by / Find the present value of the income stream in Exercise 15. Data from Exercise 15: If income
> If income is continuously collected at a rate of f(t) dollars per year and will be invested at a constant interest rate r (compounded continuously) for a period of T years, then the future value of the income is given by / Compute the future value after
> A movie theater has been charging $10.00 per person and selling about 500 tickets on a typical weeknight. After surveying their customers, the theater management estimates that for every 50 cents that they lower the price, the number of movie goers will
> A company modeled the demand curve for its product (in dollars) by the equation Use a graph to estimate the sales level when the selling price is $16. Then find (approximately) the consumer surplus for this sales level. 800,000e/S000 p = x + 20,000
> Is it possible to find a power series whose interval of convergence is [0,∞]? Explain.
> A camera company estimates that the demand function for its new digital camera is p(x) = 312e0.14x and the supply function is estimated to be pS(x) = 26e0.2x, where x is measured in thousands. Compute the maximum total surplus.
> The sum of consumer surplus and producer surplus is called the total surplus; it is one measure economists use as an indicator of the economic health of a society. Total surplus is maximized when the market for a good is in equilibrium. (a) The demand fu
> In a purely competitive market, the price of a good is naturally driven to the value where the quantity demanded by consumers matches the quantity made by producers, and the market is said to be in equilibrium. These values are the coordinates of the poi
> If a supply curve is modeled by the equation p = 125 + 0.002x2, find the producer surplus when the selling price is $625.
> The supply function pS(x) for a commodity gives the relation between the selling price and the number of units that manufacturers will produce at that price. For a higher price, manufacturers will produce more units, so pS is an increasing function of x.
> A demand curve is given by p = 450/(x + 8). Find the consumer surplus when the selling price is $10.
> A mining company estimates that the marginal cost of extracting x tons of copper ore from a mine is 0.6 + 0.008x, measured in thousands of dollars per ton. Start-up costs are $100,000. What is the cost of extracting the first 50 tons of copper? What abou
> A company estimates that the marginal revenue (in dollars per unit) realized by selling x units of a product is 48 - 0.0012x. Assuming the estimate is accurate, find the increase in revenue if sales increase from 5000 units to 10,000 units.
> Let p and q be real numbers with p (а) (р, q) (b) (р, q] (c) [р, 9) (d) [р, q]
> The hydrogen atom is composed of one proton in the nucleus and one electron, which moves about the nucleus. In the quantum theory of atomic structure, it is assumed that the electron does not move in a well-defined orbit. Instead, it occupies a state kno
> For any normal distribution, find the probability that the random variable lies within two standard deviations of the mean.
> Show that the probability density function for a normally distributed random variable has inflection points at /
> The speeds of vehicles on a highway with speed limit 100 km/h are normally distributed with mean 112 km/h and standard deviation 8 km/h. (a) What is the probability that a randomly chosen vehicle is traveling at a legal speed? (b) If police are instructe
> Boxes are labeled as containing 500 g of cereal. The machine filling the boxes produces weights that are normally distributed with standard deviation 12 g. (a) If the target weight is 500 g, what is the probability that the machine produces a box with le
> The “Garbage Project” at the University of Arizona reports that the amount of paper discarded by households per week is normally distributed with mean 9.4 lb and standard deviation 4.2 lb. What percentage of households throw out at least 10 lb of paper a
> According to the National Health Survey, the heights of adult males in the United States are normally distributed with mean 69.0 inches and standard deviation 2.8 inches. (a) What is the probability that an adult male chosen at random is between 65 inche
> REM sleep is the phase of sleep when most active dreaming occurs. In a study, the amount of REM sleep during the first four hours of sleep was described by a random variable T with probability density function where t is measured in minutes. (a) What is
> The time between infection and the display of symptoms for streptococcal sore throat is a random variable whose probabililty density function can be approximated by / otherwise (t measured in hours). (a) What is the probability that an infected patient
> If k is a positive integer, find the radius of convergence of the series (n!)* Σ (kn)! R-0
> An online retailer has determined that the average time for credit card transactions to be electronically approved is 1.6 seconds. (a) Use an exponential density function to find the probability that a customer waits less than a second for credit card ap
> Show that the median waiting time for a phone call to the company described in Example 4 is about 3.5 minutes.
> (a) Explain why the function whose graph is shown is a probability density function. (b) Use the graph to find the following probabilities: (i) P(X (ii) P(3 (c) Calculate the mean. y. 0.2 y= f(x) 0.1 2 4 8 10
> A spinner from a board game randomly indicates a real number between 0 and 10. The spinner is fair in the sense that it indicates a number in a given interval with the same probability as it indicates a number in any other interval of the same length. (a
> Let f(x) = k (3x – x2) if 0 ≤ x ≤ 3 and f(x) = 0 if x 3. (a) For what value of k is f a probability density function? (b) For that value of k, find P(X > 1). (c) Find the mean.
> Let f(x) = c/(1 = x2). (a) For what value of c is f a probability density function? (b) For that value of c, find P(21 , X , 1).
> The density function is an example of a logistic distribution. (a) Verify that f is a probability density function. (b) Find P(3 (c) Graph f. What does the mean appear to be? What about the median? e3-1 f(x) (1 + e³ =)²
> Let f(x) = 30x2 (1 – x)2 for 0 ≤ x ≤ 1 and f(x) − 0 for all other values of x. (a) Verify that f is a probability density function. (b) Find P(X <).
> Let f(t) be the probability density function for the time it takes you to drive to school in the morning, where t is measured in minutes. Express the following probabilities as integrals. (a) The probability that you drive to school in less than 15 minut
> Let f(x) be the probability density function for the lifetime of a manufacturer’s highest quality car tire, where x is measured in miles. Explain the meaning of each integral. r40,000 (а) У30,000 f(x) dx (b) 25,000 km f(x) dx my
> Von Bertalanffy’s equation states that the rate of growth in length of an individual fish is proportional to the difference between the current length L and the asymptotic length L` (in centimeters). (a) Write a differential equation that expresses this
> Psychologists interested in learning theory study learning curves. A learning curve is the graph of a function P(t), the performance of someone learning a skill as a function of the training time t. The derivative dP/dt represents the rate at which perfo
> Suppose you have just poured a cup of freshly brewed coffee with temperature 95°C in a room where the temperature is 20°C. (a) When do you think the coffee cools most quickly? What happens to the rate of cooling as time goes by? Explain. (b) Newton’s Law
> Match the differential equations with the solution graphs labeled I–IV. Give reasons for your choices. (a) y' = 1 + x? + y² (b) у' — хе * y? 1 (c) y' (d) y' = sin(xy) cos(xy) 1 + e*²+y" I II III IV yA
> The function with the given graph is a solution of one of the following differential equations. Decide which is the correct equation and justify your answer. А. у'— 1 + ху B. y' = -2xy С. у'— 1 - 2ху
> Explain why the functions with the given graphs can’t be solutions of the differential equation dy e'(y – 1)? dt (а) Уд (b) У 1
> The Fitzhugh-Nagumo model for the electrical impulse in a neuron states that, in the absence of relaxation effects, the electrical potential in a neuron v(t) obeys the differential equation where a is a positive constant such that 0 (a) For what values o
> A population is modeled by the differential equation (a) For what values of P is the population increasing? (b) For what values of P is the population decreasing? (c) What are the equilibrium solutions? dP P 1.2P dt 4200
> (a) What can you say about the graph of a solution of the equation / when x is close to 0? What if x is large? (b) Verify that all members of the family / are solutions of the differential equation / (c) Graph several members of the family of solutions
> (a) What can you say about a solution of the equation y’ = -y2 just by looking at the differential equation? (b) Verify that all members of the family /are solutions of the equation in part (a). (c) Can you think of a solution of the di
> (a) Show that every member of the family of functions y = (In x + C)/x is a solution of the differential equation / (b) Illustrate part (a) by graphing several members of the family of solutions on a common screen. (c) Find a solution of the differential
> Which of the following functions are solutions of the differential equation / у" + у— sin x? SI
> Verify that y = -t cos t = t is a solution of the initial value problem dy =y + t°sin t y(7) = 0 dt
> In Exercise 9.1.14 we considered a 958C cup of coffee in a 208C room. Suppose it is known that the coffee cools at a rate of 18C per minute when its temperature is 70°C. (a) What does the differential equation become in this case? (b) Sketch a direction
> The figure shows a circuit containing an electromotive force, a capacitor with a capacitance of C farads (F), and a resistor with a resistance of R ohms (V). The voltage drop across the capacitor is Q/C, where Q is the charge (in coulombs, C), so in this
> (a) Program your computer algebra system, using Euler’s method with step size 0.01, to calculate ys2d, where y is the solution of the initial-value problem (b) Check your work by using the CAS to draw the solution curve. y' = x' -
> Find the radius of convergence and interval of convergence of the series. n!x" Σ 1.3· 5. .... (2n – 1)
> (a) Program a calculator or computer to use Euler’s method to compute ys1d, where y(x) is the solution of the initial value problem (b) Verify that y = 2 + e2x3 is the exact solution of the differential equation. (c) Find the errors in
> (a) Use Euler’s method with step size 0.2 to estimate ys0.6d, where y(x) is the solution of the initial-value problem / (b) Repeat part (a) with step size 0.1.
> Use Euler’s method with step size 0.1 to estimate ys0.5d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.2 to estimate ys1d, where y(x) is the solution of the initial-value problem /
> Use Euler’s method with step size 0.5 to compute the approximate y-values y1, y2, y3, and y4 of the solution of the initial-value problem /
> A direction field for a differential equation is shown. Draw, with a ruler, the graphs of the Euler approximations to the solution curve that passes through the origin. Use step sizes h = 1 and h = 0.5. Will the Euler estimates be underestimates or overe
> (a) Use Euler’s method with each of the following step sizes to estimate the value of y(0.4), where y is the solution of the initial-value problem / / (b) We know that the exact solution of the initial-value problem in part (a) is y − ex. Draw, as accur
> Make a rough sketch of a direction field for the autonomous differential equation / where the graph off is as shown. How does the limiting behavior of solutions depend on the value of y(0)? y' = f(y).
> Use a computer algebra system to draw a direction field for the differential equation / Get a printout and sketch on it solutions that satisfy the initial condition y(0) = c for various values of c. For what values of c does / What are the possible value
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Find the radius of convergence and interval of convergence of the series. x" Σ 1 1 · 3 · 5 · .. 1:3. 5. ... · (2n – 1)
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point y' - x + y', (0, 0)

