Question: The outstretched hands and arms of a
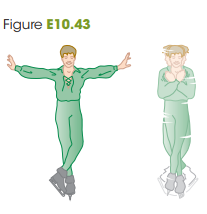
The outstretched hands and arms of a figure skater preparing for a spin can be considered a slender rod pivoting about an axis through its center (Fig. E10.43). When the skater’s hands and arms are brought in and wrapped around his body to execute the spin, the hands and arms can be considered a thin walled, hollow cylinder. His hands and arms have a combined mass of 8.0 kg. When outstretched, they span 1.8 m; when wrapped, they form a cylinder of radius 25 cm. The moment of inertia about the rotation axis of the remainder of his body is constant and equal to 0.40 kg.m2. If his original angular speed is 0.40 rev/s, what is his final angular speed?
Fig. E10.43:
Transcribed Image Text:
Figure E10.43
> The solid wood door of a gymnasium is 1.00 m wide and 2.00 m high, has total mass 35.0 kg, and is hinged along one side. The door is open and at rest when a stray basketball hits the center of the door head-on, applying an average force of 1500 N to the
> Tarzan has foolishly gotten himself into another scrape with the animals and must be rescued once again by Jane. The 60.0-kg Jane starts from rest at a height of 5.00 m in the trees and swings down to the ground using a thin, but very rigid, 30.0-kg vine
> A uniform solid cylinder with mass M and radius 2R rests on a horizontal tabletop. A string is attached by a yoke to a frictionless axle through the center of the cylinder so that the cylinder can rotate about the axle. The string runs over a disk-shaped
> A uniform, 0.0300-kg rod of length 0.400 m rotates in a horizontal plane about a fixed axis through its center and perpendicular to the rod. Two small rings, each with mass 0.0200 kg, are mounted so that they can slide along the rod. They are initially h
> A 42.0-cm-diameter wheel, consisting of a rim and six spokes, is constructed from a thin, rigid plastic material having a linear mass density of 25.0 g/cm. This wheel is released from rest at the top of a hill 58.0 m high. (a) How fast is it rolling when
> You are designing a system for moving aluminum cylinders from the ground to a loading dock. You use a sturdy wooden ramp that is 6.00 m long and inclined at 37.0o above the horizontal. Each cylinder is fitted with a light, frictionless yoke through its c
> A solid, uniform, spherical boulder starts from rest and rolls down a 50.0-m-high hill, as shown in Fig. P10.71. The top half of the hill is rough enough to cause the boulder to roll without slipping, but the lower half is covered with ice and there is n
> A solid uniform ball rolls without slipping up a hill (Fig. P10.70). At the top of the hill, it is moving horizontally, and then it goes over the vertical cliff. (a) How far from the foot of the cliff does the ball land, and how fast is it moving just be
> A basketball (which can be closely modeled as a hollow spherical shell) rolls down a mountainside into a valley and then up the opposite side, starting from rest at a height H0 above the bottom. In Fig. P10.69, the rough part of the terrain prevents slip
> A thin-walled, hollow spherical shell of mass m and radius r starts from rest and rolls without slipping down a track (Fig. P10.68). Points A and B are on a circular part of the track having radius R. The diameter of the shell is very small compared to h
> A yo-yo is made from two uniform disks, each with mass m and radius R, connected by a light axle of radius b. A light, thin string is wound several times around the axle and then held stationary while the yo-yo is released from rest, dropping as the stri
> When a tall, heavy refrigerator is pushed across a rough floor, what factors determine whether it slides or tips?
> You complain about fire safety to the landlord of your high-rise apartment building. He is willing to install an evacuation device if it is cheap and reliable, and he asks you to design it. Your proposal is to mount a large wheel (radius 0.400 m) on an a
> Two weights are connected by a very light, flexible cord that passes over an 80.0-N frictionless pulley of radius 0.300 m. The pulley is a solid uniform disk and is supported by a hook connected to the ceiling (Fig. P10.65). What force does the ceiling e
> A lawn roller in the form of a thin-walled, hollow cylinder with mass M is pulled horizontally with a constant horizontal force F applied by a handle attached to the axle. If it rolls without slipping, find the acceleration and the friction force.
> Two metal disks, one with radius R1 = 2.50 cm and mass M1 = 0.80 kg and the other with radius R2 = 5.00 cm and mass M2 = 1.60 kg, are welded together and mounted on a frictionless axis through their common center, as in Problem 9.77. (a) A light string i
> A block with mass m = 5.00 kg slides down a surface inclined 36.9° to the horizontal (Fig. P10.62). The coefficient of kinetic friction is 0.25. A string attached to the block is wrapped around a flywheel on a fixed axis at O. The flywheel has
> A large 16.0-kg roll of paper with radius R = 18.0 cm rests against the wall and is held in place by a bracket attached to a rod through the center of the roll (Fig. P10.61). The rod turns without friction in the bracket, and the moment of inertia of the
> The mechanism shown in Fig. P10.60 is used to raise a crate of supplies from a ship’s hold. The crate has total mass 50 kg. A rope is wrapped around a wooden cylinder that turns on a metal axle. The cylinder has radius 0.25 m and moment of inertia I = 2.
> Figure P10.59 illustrates an Atwood’s machine. Find the linear accelerations of blocks A and B, the angular acceleration of the wheel C, and the tension in each side of the cord if there is no slipping between the cord and the surface o
> You are designing a simple elevator system for an old warehouse that is being converted to loft apartments. A 22,500-N elevator is to be accelerated upward by connecting it to a counterweight by means of a light (but strong!) cable passing over a solid u
> A thin, uniform, 3.80-kg bar, 80.0 cm long, has very small 2.50-kg balls glued on at either end (Fig. P10.57). It is supported horizontally by a thin, horizontal, frictionless axle passing through its center and perpendicular to the bar. Suddenly the rig
> In Example 10.10 (Section 10.6) the angular speed v changes, and this must mean that there is nonzero angular acceleration. But there is no torque about the rotation axis if the forces the professor applies to the weights are directly, radially inward. T
> A uniform, 8.40-kg, spherical shell 50.0 cm in diameter has four small 2.00-kg masses attached to its outer surface and equally spaced around it. This combination is spinning about an axis running through the center of the sphere and two of the small mas
> A grindstone in the shape of a solid disk with diameter 0.520 m and a mass of 50.0 kg is rotating at 850 rev/min. You press an ax against the rim with a normal force of 160 N (Fig. P10.54), and the grindstone comes to rest in 7.50 s. Find the coefficient
> A 50.0-kg grindstone is a solid disk 0.520 m in diameter. You press an ax down on the rim with a normal force of 160 N (Fig. P10.54). The coefficient of kinetic friction between the blade and the stone is 0.60, and there is a constant friction torque of
> In a simplified version of the musculature action in leg raises, the abdominal muscles pull on the femur (thigh bone) to raise the leg by pivoting it about one end (Fig. P11.53). When you are lying horizontally, these muscles make an angle of approximate
> A loaded cement mixer drives onto an old drawbridge, where it stalls with its center of gravity three-quarters of the way across the span. The truck driver radios for help, sets the handbrake, and waits. Meanwhile, a boat approaches, so the drawbridge is
> A therapist tells a 74-kg patient with a broken leg that he must have his leg in a cast suspended horizontally. For minimum discomfort, the leg should be supported by a vertical strap attached at the center of mass of the leg–cast syste
> End A of the bar AB in Fig. P11.50 rests on a frictionless horizontal surface, and end B is hinged. A horizontal force
> You open a restaurant and hope to entice customers by hanging out a sign (Fig. P11.49). The uniform horizontal beam supporting the sign is 1.50 m long, has a mass of 16.0 kg, and is hinged to the wall. The sign itself is uniform with a mass of 28.0 kg an
> A claw hammer is used to pull a nail out of a board (Fig. P11.48). The nail is at an angle of 60° to the board, and a force F S 1 of magnitude 400 N applied to the nail is required to pull it from the board. The hammer head contacts the board at point A,
> A uniform, 255-N rod that is 2.00 m long carries a 225-N weight at its right end and an unknown weight W toward the left end (Fig. P11.47). When W is placed 50.0 cm from the left end of the rod, the system just balances horizontally when the fulcrum is l
> Why is a tapered water glass with a narrow base easier to tip over than a glass with straight sides? Does it matter whether the glass is full or empty?
> Suppose you could use wheels of any type in the design of a soapbox-derby racer (an unpowered, four-wheel vehicle that coasts from rest down a hill). To conform to the rules on the total weight of the vehicle and rider, should you design with large massi
> A uniform, 8.0-m, 1150-kg beam is hinged to a wall and supported by a thin cable attached 2.0 m from the free end of the beam (Fig. P11.46). The beam is supported at an angle of 30.0° above the horizontal. (a) Draw a free-body diagram of the b
> Mountaineers often use a rope to lower themselves down the face of a cliff (this is called rappelling). They do this with their body nearly horizontal and their feet pushing against the cliff (Fig. P11.45). Suppose that an 82.0-kg climber, who is 1.90 m
> Sir Lancelot rides slowly out of the castle at Camelot and onto the 12.0-m-long drawbridge that passes over the moat (Fig. P11.44). Unbeknownst to him, his enemies have partially severed the vertical cable holding up the front end of the bridge so that i
> A box of negligible mass rests at the left end of a 2.00-m, 25.0-kg plank (Fig. P11.43). The width of the box is 75.0 cm, and sand is to be distributed uniformly throughout it. The center of gravity of the non-uniform plank is 50.0 cm from the right end.
> A door 1.00 m wide and 2.00 m high weighs 330 N and is supported by two hinges, one 0.50 m from the top and the other 0.50 m from the bottom. Each hinge supports half the total weight of the door. Assuming that the door’s center of gravity is at its cent
> A 350-N, uniform, 1.50-m bar is suspended horizontally by two vertical cables at each end. Cable A can support a maximum tension of 500.0 N without breaking, and cable B can support up to 400.0 N. You want to place a small weight on this bar. (a) What is
> A 60.0-cm, uniform, 50.0-N shelf is supported horizontally by two vertical wires attached to the sloping ceiling (Fig. E11.8). A very small 25.0-N tool is placed on the shelf midway between the points where the wires are attached to it. Find the tension
> Two people carry a heavy electric motor by placing it on a light board 2.00 m long. One person lifts at one end with a force of 400 N, and the other lifts the opposite end with a force of 600 N. (a) What is the weight of the motor, and where along the bo
> Two people are carrying a uniform wooden board that is 3.00 m long and weighs 160 N. If one person applies an upward force equal to 60 N at one end, at what point does the other person lift? Begin with a free-body diagram of the board.
> A ladder carried by a fire truck is 20.0 m long. The ladder weighs 3400 N and its center of gravity is at its center. The ladder is pivoted at one end (A) about a pin (Fig. E11.5); ignore the friction torque at the pin. The ladder is raised into position
> A student is sitting on a frictionless rotating stool with her arms outstretched as she holds equal heavy weights in each hand. If she suddenly lets go of the weights, will her angular speed increase, stay the same, or decrease? Explain.
> A steel cable with cross-sectional area 3.00 cm2 has an elastic limit of 2.40 × 108 Pa. Find the maximum upward acceleration that can be given a 1200-kg elevator supported by the cable if the stress is not to exceed one-third of the elastic limit.
> A 4.0-m-long steel wire has a cross-sectional area of 0.050 cm2. Its proportional limit has a value of 0.0016 times its Young’s modulus. Its breaking stress has a value of 0.0065 times its Young’s modulus. The wire is fastened at its upper end and hangs
> A solid wood door 1.00 m wide and 2.00 m high is hinged along one side and has a total mass of 40.0 kg. Initially open and at rest, the door is struck at its center by a handful of sticky mud with mass 0.500 kg, traveling perpendicular to the door at 12.
> A diver comes off a board with arms straight up and legs straight down, giving her a moment of inertia about her rotation axis of 18 kg.m2. She then tucks into a small ball, decreasing this moment of inertia to 3.6 kg.m2. While tucked, she makes two comp
> Under some circumstances, a star can collapse into an extremely dense object made mostly of neutrons and called a neutron star. The density of a neutron star is roughly 1014 times as great as that of ordinary solid matter. Suppose we represent the star a
> A small block on a frictionless, horizontal surface has a mass of 0.0250 kg. It is attached to a massless cord passing through a hole in the surface (Fig. E10.40). The block is originally revolving at a distance of 0.300 m from the hole with an angular s
> A hollow, thin-walled sphere of mass 12.0 kg and diameter 48.0 cm is rotating about an axle through its center. The angle (in radians) through which it turns as a function of time (in seconds) is given by
> (a) Calculate the magnitude of the angular momentum of the earth in a circular orbit around the sun. Is it reasonable to model it as a particle? (b) Calculate the magnitude of the angular momentum of the earth due to its rotation around an axis through t
> Find the magnitude of the angular momentum of the second hand on a clock about an axis through the center of the clock face. The clock hand has a length of 15.0 cm and a mass of 6.00 g. Take the second hand to be a slender rod rotating with constant angu
> If two spinning objects have the same angular momentum, do they necessarily have the same rotational kinetic energy? If they have the same rotational kinetic energy, do they necessarily have the same angular momentum? Explain.
> A woman with mass 50 kg is standing on the rim of a large disk that is rotating at 0.80 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.0 m. Calculate the magnitude of the total angular momentum of the woman–disk system. (As
> A 2.00-kg rock has a horizontal velocity of magnitude 12.0 m/s when it is at point P in Fig. E10.35. (a) At this instant, what are the magnitude and direction of its angular momentum relative to point O? (b) If the only force acting on the rock is its we
> An airplane propeller is 2.08 m in length (from tip to tip) and has a mass of 117 kg. When the airplane’s engine is first started, it applies a constant torque of 1950 N.m to the propeller, which starts from rest. (a) What is the angular acceleration of
> (a) Compute the torque developed by an industrial motor whose output is 150 kW at an angular speed of 4000 rev/min. (b) A drum with negligible mass, 0.400 m in diameter, is attached to the motor shaft, and the power output of the motor is used to raise a
> An electric motor consumes 9.00 kJ of electrical energy in 1.00 min. If one-third of this energy goes into heat and other forms of internal energy of the motor, with the rest going to the motor output, how much torque will this engine develop if you run
> A 2.80-kg grinding wheel is in the form of a solid cylinder of radius 0.100 m. (a) What constant torque will bring it from rest to an angular speed of 1200 rev/min in 2.5 s? (b) Through what angle has it turned during that time? (c) Use Eq. (10.21) to ca
> An engine delivers 175 h p to an aircraft propeller at 2400 rev/min. (a) How much torque does the aircraft engine provide? (b) How much work does the engine do in one revolution of the propeller?
> A playground merry-go-round has radius 2.40 m and moment of inertia 2100 kg#m2 about a vertical axle through its center, and it turns with negligible friction. (a) A child applies an 18.0-N force tangentially to the edge of the merry-go-round for 15.0 s.
> A bicycle racer is going downhill at 11.0 m/s when, to his horror, one of his 2.25-kg wheels comes off as he is 75.0 m above the foot of the hill. We can model the wheel as a thin-walled cylinder 85.0 cm in diameter and ignore the small mass of the spoke
> A size-5 soccer ball of diameter 22.6 cm and mass 426 g rolls up a hill without slipping, reaching a maximum height of 5.00 m above the base of the hill. We can model this ball as a thin-walled hollow sphere. (a) At what rate was it rotating at the base
> If the earth’s climate continues to warm, ice near the poles will melt, and the water will be added to the oceans. What effect will this have on the length of the day? Justify your answer.
> A bowling ball rolls without slipping up a ramp that slopes upward at an angle b to the horizontal (see Example 10.7 in Section 10.3). Treat the ball as a uniform solid sphere, ignoring the finger holes. (a) Draw the free body diagram for the ball. Expla
> A thin, light string is wrapped around the outer rim of a uniform hollow cylinder of mass 4.75 kg having inner and outer radii as shown in Fig. E10.25. The cylinder is then released from rest. (a) How far must the cylinder fall before its center is movin
> A uniform marble rolls down a symmetrical bowl, starting from rest at the top of the left side. The top of each side is a distance h above the bottom of the bowl. The left half of the bowl is rough enough to cause the marble to roll without slipping, but
> A 392-N wheel comes off a moving truck and rolls without slipping along a highway. At the bottom of a hill it is rotating at 25.0 rad/s. The radius of the wheel is 0.600 m, and its moment of inertia about its rotation axis is 0.800MR2. Friction does work
> A hollow, spherical shell with mass 2.00 kg rolls without slipping down a 38.0° slope. (a) Find the acceleration, the friction force, and the minimum coefficient of friction needed to prevent slipping. (b) How would your answers to part (a) change if the
> A solid ball is released from rest and slides down a hillside that slopes downward at 65.0° from the horizontal. (a) What minimum value must the coefficient of static friction between the hill and ball surfaces have for no slipping to occur? (b) Would th
> A string is wrapped several times around the rim of a small hoop with radius 8.00 cm and mass 0.180 kg. The free end of the string is held in place and the hoop is released from rest (Fig. E10.20). After the hoop has descended 75.0 cm, calculate (a) the
> What fraction of the total kinetic energy is rotational for the following objects rolling without slipping on a horizontal surface? (a) A uniform solid cylinder; (b) a uniform sphere; (c) a thin-walled, hollow sphere; (d) a hollow cylinder with outer rad
> We can roughly model a gymnastic tumbler as a uniform solid cylinder of mass 75 kg and diameter 1.0 m. If this tumbler rolls forward at 0.50 rev/s, (a) how much total kinetic energy does he have, and (b) what percent of his total kinetic energy is rotati
> A 2.20-kg hoop 1.20 m in diameter is rolling to the right without slipping on a horizontal floor at a steady 2.60 rad/s. (a) How fast is its center moving? (b) What is the total kinetic energy of the hoop? (c) Find the velocity vector of each of the foll
> You are standing at the center of a large horizontal turntable in a carnival funhouse. The turntable is set rotating on frictionless bearings, and it rotates freely (that is, there is no motor driving the turntable). As you walk toward the edge of the tu
> A 12.0-kg box resting on a horizontal, frictionless surface is attached to a 5.00-kg weight by a thin, light wire that passes over a frictionless pulley (Fig. E10.16). The pulley has the shape of a uniform solid disk of mass 2.00 kg and diameter 0.500 m.
> A wheel rotates without friction about a stationary horizontal axis at the center of the wheel. A constant tangential force equal to 80.0 N is applied to the rim of the wheel. The wheel has radius 0.120 m. Starting from rest, the wheel has an angular spe
> A 15.0-kg bucket of water is suspended by a very light rope wrapped around a solid uniform cylinder 0.300 m in diameter with mass 12.0 kg. The cylinder pivots on a frictionless axle through its center. The bucket is released from rest at the top of a wel
> A 2.00-kg textbook rests on a frictionless, horizontal surface. A cord attached to the book passes over a pulley whose diameter is 0.150 m, to a hanging book with mass 3.00 kg. The system is released from rest, and the books are observed to move 1.20 m i
> A stone is suspended from the free end of a wire that is wrapped around the outer rim of a pulley, similar to what is shown in Fig. 10.10. The pulley is a uniform disk with mass 10.0 kg and radius 30.0 cm and turns on frictionless bearings. You measure t
> A machine part has the shape of a solid uniform sphere of mass 225 g and diameter 3.00 cm. It is spinning about a frictionless axle through its center, but at one point on its equator it is scraping against metal, resulting in a friction force of 0.0200
> A cord is wrapped around the rim of a solid uniform wheel 0.250 m in radius and of mass 9.20 kg. A steady horizontal pull of 40.0 N to the right is exerted on the cord, pulling it off tangentially from the wheel. The wheel is mounted on frictionless bear
> The flywheel of an engine has moment of inertia 1.60 kg.m2 about its rotation axis. What constant torque is required to bring it up to an angular speed of 400 rev/min in 8.00 s, starting from rest?
> A uniform disk with mass 40.0 kg and radius 0.200 m is pivoted at its center about a horizontal, frictionless axle that is stationary. The disk is initially at rest, and then a constant force F = 30.0 N is applied tangent to the rim of the disk. (a) What
> A machinist is using a wrench to loosen a nut. The wrench is 25.0 cm long, and he exerts a 17.0-N force at the end of the handle at 37° with the handle (Fig. E10.7). (a) What torque does the machinist exert about the center of the nut? (b) Wha
> A ball is rolling along at speed v without slipping on a horizontal surface when it comes to a hill that rises at a constant angle above the horizontal. In which case will it go higher up the hill: if the hill has enough friction to prevent slipping or i
> A metal bar is in the x y-plane with one end of the bar at the origin. A force
> One force acting on a machine part is F =(-5.00 N)
> Three forces are applied to a wheel of radius 0.350 m, as shown in Fig. E10.4. One force is perpendicular to the rim, one is tangent to it, and the other one makes a 40.0° angle with the radius. What is the net torque on the wheel due to these
> A square metal plate 0.180 m on each side is pivoted about an axis through point O at its center and perpendicular to the plate (Fig. E10.3). Calculate the net torque about this axis due to the three forces shown in the figure if the magnitudes of the fo
> Calculate the net torque about point O for the two forces applied as in Fig. E10.2. The rod and both forces are in the plane of the page. Fig. E10.2: Figure E10.2 F2 = 12.0 N F, = 8.00 N 30.0° K-2.00 mK 3.00 m
> Calculate the torque (magnitude and direction) about point O due to the force
> Scientists have found evidence that Mars may once have had an ocean 0.500 km deep. The acceleration due to gravity on Mars is 3.71 m/s2. (a) What would be the gauge pressure at the bottom of such an ocean, assuming it was freshwater? (b) To what depth wo
> Black smokers are hot volcanic vents that emit smoke deep in the ocean floor. Many of them teem with exotic creatures, and some biologists think that life on earth may have begun around such vents. The vents range in depth from about 1500 m to 3200 m bel
> A hollow cylindrical copper pipe is 1.50 m long and has an outside diameter of 3.50 cm and an inside diameter of 2.50 cm. How much does it weigh?
> (a) What is the average density of the sun? (b) What is the average density of a neutron star that has the same mass as the sun but a radius of only 20.0 km?
> A hoop, a uniform solid cylinder, a spherical shell, and a uniform solid sphere are released from rest at the top of an incline. What is the order in which they arrive at the bottom of the incline? Does it matter whether or not the masses and radii of th

