Question: The preceding problem was an artificial
The preceding problem was an artiï¬cial model for the charging capacitor, designed to avoid complications associated with the current spreading out over the surface of the plates. For a more realistic model, imagine thin wires that connect to the centers of the plates (Fig. 7.46a). Again, the current I is constant, the radius of the capacitor is a, and the separation of the plates is w(a) Find the electric ï¬eld between the plates, as a function of t .
(b) Find the displacement current through a circle of radius s in the plane mid- way between the plates. Using this circle as your “Amperian loop,†and the flat surface that spans it, ï¬nd the magnetic ï¬eld at a distance s from the axis.
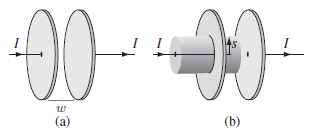
(c) Repeat part (b), but this time use the cylindrical surface in Fig. 7.46(b), which is open at the right end and extends to the left through the plate and terminates outside the capacitor. Notice that the displacement current through this surface is zero, and there are two contributions to Ienc.22
> Picture the electron as a uniformly charged spherical shell, with charge e and radius R, spinning at angular velocity ω. (a) Calculate the total energy contained in the electromagnetic fields. (b) Calculate the total angular momentum contained in the field
> (a) Check the divergence theorem for the function / using as your volume the sphere of radius R, centered at the origin. (b) Do the same for / (If the answer surprises you, look back at Prob. 1.16.)
> A sphere of radius R carries a uniform polarization P and a uniform magnetization M (not necessarily in the same direction). Find the electromagnetic momentum of this configuration. [Answer: (4/9)πμ0 R3(M × P)]
> A point charge q is located at the center of a toroidal coil of rectangular cross section, inner radius a, outer radius a+w, and height h, which carries a total of N tightly-wound turns and current I . (a) Find the electromagnetic momentum p of this confi
> An infinitely long cylindrical tube, of radius a, moves at constant speed v along its axis. It carries a net charge per unit length λ, uniformly distributed over its surface. Surrounding it, at radius b, is another cylinder, moving with the same velocity
> A very long solenoid of radius a, with n turns per unit length, carries a current Is . Coaxial with the solenoid, at radius b ((a, is a circular ring of wire, with resistance R. When the current in the solenoid is (gradually) decreased, a current Ir is i
> Derive Eq. 8.43. [Hint: Use the method of Section 7.2.4, building the two currents up from zero to their final values.]
> Derive Eq. 8.39. [Hint: Treat the lower loop as a magnetic dipole.]
> Imagine an iron sphere of radius R that carries a charge Q and a uniform magnetization M = M zˆ. The sphere is initially at rest. (a) Compute the angular momentum stored in the electromagnetic fields. (b) Suppose the sphere is g
> Calculate the power (energy per unit time) transported down the cables of Ex. 7.13 and Prob. 7.62, assuming the two conductors are held at potential difference V, and carry current I (down one and back up the other).
> An infinite number of different surfaces can be fit to a given boundary line, and yet, in defining the magnetic flux through a loop, / I never specified the particular surface to be used. Justify this apparent oversight.
> A square loop of wire (side a) lies on a table, a distance s from a very long straight wire, which carries a current I , as shown in Fig. 7.18. (a) Find the flux of B through the loop. (b) If someone now pulls the loop directly away from t
> Express the unit vectors rˆ, θˆ, φˆ in terms of xˆ, yˆ, zˆ (that is, derive Eq. 1.64). Check your answers several ways (rˆ · rˆ =? 1, θˆ · φˆ =? 0, rˆ × θˆ =? φˆ,.. .). Also work out the inverse formulas, giving xˆ, yˆ, zˆ in terms of rˆ, θˆ,
> A metal bar of mass m slides frictionlessly on two parallel conducting rails a distance l apart (Fig. 7.17). A resistor R is connected across the rails, and a uniform magnetic field B, pointing into the page, fills the entir
> (a) Show that Maxwell’s equations with magnetic charge (Eq. 7.44) are invariant under the duality transformation where / and α is an arbitrary rotation angle in “E/B-space.” Charge and c
> Prove Alfven’s theorem: In a perfectly conducting fluid (say, a gas of free electrons), the magnetic flux through any closed loop moving with the fluid is constant in time. (The magnetic &ium
> A certain transmission line is constructed from two thin metal “rib- bons,” of width w, a very small distance h
> The magnetic field of an infinite straight wire carrying a steady cur- rent I can be obtained from the displacement current term in the Ampère/Maxwell law, as follows: Picture the current as consisting of a uniform line charge λ moving along the z axis at
> Suppose J(r) is constant in time but ρ(r, t) is not—conditions that might prevail, for instance, during the charging of a capacitor. (a) Show that the charge density at any particular point is a linear function of time: Ï
> A rectangular loop of wire is situated so that one end (height h) is between the plates of a parallel-plate capacitor (Fig. 7.9), oriented parallel to the field E. The other end is way outside, where the field is essentially
> An infinite wire runs along the z axis; it carries a current I (z) that is a function of z (but not of t ), and a charge density λ(t) that is a function of t (but not of z). (a) By examining the charge flowing into a segment dz in a time dt , show that dλ/
> A transformer (Prob. 7.57) takes an input AC voltage of amplitude V1, and delivers an output voltage of amplitude V2, which is determined by the turns ratio (V2/ V1 N2/N1). If N2 > N1, the output voltage is greater than the input voltage. Why doesn’t thi
> Two coils are wrapped around a cylindrical form in such a way that the same flux passes through every turn of both coils. (In practice this is achieved by inserting an iron core through the cylinder; this has the effect of concentrating th
> Find formulas for r,θ,φ in terms of x, y, z (the inverse, in other words, of Eq. 1.62).
> (a) Use the Neumann formula (Eq. 7.23) to calculate the mutual inductance of the configuration in Fig. 7.37, assuming a is very small /Compare your answer to Prob. 7.22. (b) For the general case (not assuming a is small), show that where
> In the discussion of motional emf (Sect. 7.1.3) I assumed that the wire loop (Fig. 7.10) has a resistance R; the current generated is then I= v Bh/R. But what if the wire is made out of perfectly conducting material, so that R is zero? In that case, the
> A circular wire loop (radius r , resistance R) encloses a region of uniform magnetic field, B, perpendicular to its plane. The field (occupying the shaded region in Fig. 7.56) increases linearly with time (B= α
> The current in a long solenoid is increasing linearly with time, so the flux is proportional to t : Ф =αt . Two voltmeters are connected to diametrically opposite points ( A and B), together with resistors (R1 and
> An atomic electron (charge q) circles about the nucleus (charge Q) in an orbit of radius r ; the centripetal acceleration is provided, of course, by the Coulomb attraction of opposite charges. Now a small magnetic field dB is slowly turned on, perpendicu
> An infinite wire carrying a constant current / direction is moving in the y direction at a constant speed v. Find the electric field, in the quasistatic approximation, at the instant the wire coincides with the z axis (Fig. 7.54). /
> Electrons undergoing cyclotron motion can be sped up by increasing the magnetic field; the accompanying electric field will impart tangential acceleration. This is the principle of the betatron. One would like to keep the radius of the orbit constant dur
> A battery of emf ε and internal resistance r is hooked up to a variable “load” resistance, R. If you want to deliver the maximum possible power to the load, what resistance R should you choose? (You can’t change E and r , of course.)
> (a) Referring to Prob. 5.52(a) and Eq. 7.18, show that for Faraday-induced electric fields. Check this result by taking the divergence and curl of both sides. (b) A spherical shell of radius R carries a uniform surface charge σ . It spins abou
> Refer to Prob. 7.11 (and use the result of Prob. 5.42): How long does is take a falling circular ring (radius a, mass m, resistance R) to cross the bottom of the magnetic field B, at its (changing) terminal velocity?
> (a) Show that / (b) Show that
> A perfectly conducting spherical shell of radius a rotates about the z axis with angular velocity ω, in a uniform magnetic field Calculate the emf developed between the “north pole” and the e
> If a magnetic dipole levitating above an infinite superconducting plane (Prob. 7.45) is free to rotate, what orientation will it adopt, and how high above the surface will it float?
> A familiar demonstration of superconductivity (Prob. 7.44) is the levitation of a magnet over a piece of superconducting material. This phenomenon can be analyzed using the method of images.31 Treat the magnet as a perfect dipole m, a height z above the
> In a perfect conductor, the conductivity is infinite, so E=0 (Eq. 7.3), and any net charge resides on the surface (just as it does for an imperfect conductor, in electrostatics). (a) Show that the magnetic field is constant (∂B/∂t=0), inside a perfect cond
> The magnetic field outside a long straight wire carrying a steady current I is The electric field inside the wire is uniform: where ρ is the resistivity and a is the radius (see Exs. 7.1 and 7.3). Question: What i
> A rare case in which the electrostatic field E for a circuit can actually be calculated is the following:28 Imagine an infinitely long cylindrical sheet, of uniform resistivity and radius a. A slot (corresponding to the batt
> Two long, straight copper pipes, each of radius a, are held a distance 2d apart (see Fig. 7.50). One is at potential V0, the other at V0. The space surrounding the pipes is filled with weakly conducting material of conductivity σ
> Sea water at frequency / Hz has permittivity / permeability μ=μ0, and resistivity ρ=0.23 Ω m. What is the ratio of conduction current to displacement current? [Hint: Consider a parallel-plate capacitor immersed in sea water and driven by a voltage V0
> Suppose the conductivity of the material separating the cylinders in Ex. 7.2 is not uniform; specifically, σ(s)=k/s, for some constant k. Find the resistance between the cylinders. [Hint: Because σ is a function of position, Eq. 7.5 does not hold, the cha
> Suppose a magnetic monopole qm passes through a resistanceless loop of wire with self-inductance L. What current is induced in the loop?27
> Check Corollary 1 by using the same function and boundary line as in Ex. 1.11, but integrating over the five faces of the cube in Fig. 1.35. The back of the cube is open.
> Assuming that “Coulomb’s law” for magnetic charges (qm ) reads work out the force law for a monopole qm moving with velocity v through electric and magnetic fields E and B.26
> Suppose / (The theta function is defined in Prob. 1.46b). Show that these fields satisfy all of Maxwell’s equations, and determine ρ and J. Describe the physical situation that gives rise to these fields.
> Refer to Prob. 7.16, to which the correct answer was / (a) Find the displacement current density Jd . (b) Integrate it to get the total displacement current, (c) Compare Id and I . (What’s their ratio?) If the outer cylinder were, say,
> A fat wire, radius a, carries a constant current I , uniformly distributed over its cross section. A narrow gap in the wire, of width w
> An infinite cylinder of radius R carries a uniform surface charge σ . We propose to set it spinning about its axis, at a final angular velocity ωf . How much work will this take, per unit length? Do it two ways, and compare your answers: (a) Find the magne
> Two tiny wire loops, with areas a1 and a2, are situated a displacement r apart (Fig. 7.42). (a) Find their mutual inductance. [Hint: Treat them as magnetic dipoles, and use Eq. 5.88.] Is your formula consistent with Eq. 7.24? (b) Suppose a current I1 is
> Suppose the circuit in Fig. 7.41 has been connected for a long time when suddenly, at time t = 0, switch S is thrown from A to B, bypassing the battery. (a) What is the current at any subsequent time t ? (b) What is the total energy delivered to the resi
> A long cable carries current in one direction uniformly distributed over its (circular) cross section. The current returns along the surface (there is a very thin insulating sheath separating the currents). Find the self-inductance per unit length.
> (a) Two metal objects are embedded in weakly conducting material of conductivity σ (Fig. 7.6). Show that the resistance between them is related to the capacitance of the arrangement by / (b) Suppose you connected a battery between 1 and 2, an
> Test Stokes’ theorem for the function v = (xy) xˆ + (2yz) yˆ + (3zx) zˆ, using the triangular shaded area of Fig. 1.34.
> Calculate the energy stored in the toroidal coil of Ex. 7.11, by applying Eq. 7.35. Use the answer to check Eq. 7.28.
> Find the energy stored in a section of length l of a long solenoid (radius R, current I , n turns per unit length), (a) using Eq. 7.30 (you found L in Prob. 7.24); (b) using Eq. 7.31 (we worked out A in Ex. 5.12); (c) using Eq. 7.35; (d) using Eq. 7.3
> A capacitor C is charged up to a voltage V and connected to an inductor L, as shown schematically in Fig. 7.39. At time t= 0, the switch S is closed. Find the current in the circuit as a function of time. How does your answer change if a resistor R is in
> An alternating current I (t)= I0 cos(ωt ) (amplitude 0.5 A, frequency 60 Hz) flows down a straight wire, which runs along the axis of a toroidal coil with rectangular cross section (inner radius 1 cm, outer radius 2 cm, height 1 cm, 1000 turns). The coil
> Try to compute the self-inductance of the “hairpin” loop shown in Fig. 7.38. (Neglect the contribution from the ends; most of the flux comes from the long straight section.) You’ll run
> Find the self-inductance per unit length of a long solenoid, of radius R, carrying n turns per unit length.
> A square loop of wire, of side a, lies midway between two long wires, 3a apart, and in the same plane. (Actually, the long wires are sides of a large rectangular loop, but the short ends are so far away that they can be neglected.) A clock- wise current
> A small loop of wire (radius a) is held a distance z above the center of a large loop (radius b), as shown in Fig. 7.37. The planes of the two loops are parallel, and perpendicular to the common axis. (a) Suppose current I flows in the big loop. Find the
> Imagine a uniform magnetic field, pointing in the z direction and filling all space / A positive charge is at rest, at the origin. Now somebody turns off the magnetic field, thereby inducing an electric field. In what direction does the charge move?16
> Where is ∂B/∂t nonzero, in Figure 7.21(b)? Exploit the analogy between Faraday’s law and Ampère’s law to sketch (qualitatively) the electric field
> Test the divergence theorem for the function v = (xy) xˆ + (2yz) yˆ+ (3zx) zˆ. Take as your volume the cube shown in Fig. 1.30, with sides of length 2.
> A capacitor C has been charged up to potential V0; at time t=0, it is connected to a resistor R, and begins to discharge (Fig. 7.5a). (a) Determine the charge on the capacitor as a function of time, Q(t). What is the current through the resistor, I (t)?
> A toroidal coil has a rectangular cross section, with inner radius a, outer radius a+w, and height h. It carries a total of N tightly wound turns, and the current is increasing at a constant rate (dI/dt=k). If w and h are both much less than a, find the e
> A square loop, side a, resistance R, lies a distance s from an infinite straight wire that carries current I (Fig. 7.29). Now someone cuts the wire, so I drops to zero. In what direction does the induced current in the square loop ï&n
> A long solenoid of radius a, carrying n turns per unit length, is looped by a wire with resistance R, as shown in Fig. 7.28. (a) If the current in the solenoid is increasing at a constant rate (dI/dt= k), what current flows in the loop, an
> An alternating current I=I0 cos (ωt) flows down a long straight wire, and returns along a coaxial conducting tube of radius a. (a) In what direction does the induced electric field point (radial, circumferential, or longitudinal)? (b) Assuming that the fiel
> A long solenoid with radius a and n turns per unit length carries a time-dependent current I (t) in the φˆ direction. Find the electric field (magnitude and direction) at a distance s from the axis (both inside and outside the solenoid), in the quasistati
> As a lecture demonstration a short cylindrical bar magnet is dropped down a vertical aluminum pipe of slightly larger diameter, about 2 meters long. It takes several seconds to emerge at the bottom, whereas an otherwise identical piece of unmagnetized ir
> A square loop of wire, with sides of length a, lies in the first quadrant of the xy plane, with one corner at the origin. In this region, there is a nonuniform time-dependent magnetic field / (where k is a constant). Find the emf induced in the loop.
> A long solenoid, of radius a, is driven by an alternating current, so that the field inside is sinusoidal: / A circular loop of wire, of radius a/2 and resistance R, is placed inside the solenoid, and coaxial with it. Find the current induced in the loop
> A square loop is cut out of a thick sheet of aluminum. It is then placed so that the top portion is in a uniform magnetic field B, and is allowed to fall under gravity (Fig. 7.20). (In the diagram, shading indicates the fiel
> Check the fundamental theorem for gradients, using T = x 2 + 4xy + 2yz3, the points a = (0, 0, 0), b = (1, 1, 1), and the three paths in Fig. 1.28: (a) (0, 0, 0) → (1, 0, 0) → (1, 1, 0) → (1, 1, 1); (
> A square loop (side a) is mounted on a vertical shaft and rotated at angular velocity ω (Fig. 7.19). A uniform magnetic field B points to the right. Find the E(t) for this alternating current generator.
> Two concentric metal spherical shells, of radius a and b, respectively, are separated by weakly conducting material of conductivity σ (Fig. 7.4a). (a) If they are maintained at a potential difference V, what current flows from o
> A short circular cylinder of radius a and length L carries a “frozen-in” uniform magnetization M parallel to its axis. Find the bound current, and sketch the magnetic field of the cylinder. (Make three sketches: one for L ((a, one for L
> A long circular cylinder of radius R carries a magnetization M = ks2 φˆ, where k is a constant, s is the distance from the axis, and φˆ is the usual azimuthal unit vector (Fig. 6.13). Find the
> An infinitely long circular cylinder carries a uniform magnetization M parallel to its axis. Find the magnetic field (due to M) inside and outside the cylinder.
> Of the following materials, which would you expect to be paramagnetic and which diamagnetic: aluminum, copper, copper chloride (CuCl2), carbon, lead, nitrogen (N2), salt (NaCl), sodium, sulfur, water? (Actually, copper is slightly diamagnetic; otherwise
> A uniform current density J = J0 zˆ fills a slab straddling the yz plane, from x = −a to x = +a. A magnetic dipole m = m0 xˆ is situated at the origin. (a) Find the force on the dipole, using Eq. 6.3. (b) Do the same for a dipole pointing in the y directi
> Derive Eq. 6.3. [Here’s one way to do it: Assume the dipole is an infinitesimal square, of side ε (if it’s not, chop it up into squares, and apply the argument to each one). Choose axes as s
> Find the force of attraction between two magnetic dipoles, m1 and m2, oriented as shown in Fig. 6.7, a distance r apart, (a) using Eq. 6.2, and (b) using Eq. 6.3.
> You are asked to referee a grant application, which proposes to determine whether the magnetization of iron is due to “Ampère” dipoles (current loops) or “Gilbert” dipoles (separated magnetic monopoles). The experiment will involve a cylinder of iron (ra
> Calculate the volume integral of the function T z2 over the tetrahedron with corners at (0,0,0), (1,0,0), (0,1,0), and (0,0,1).
> A magnetic dipole m is imbedded at the center of a sphere (radius R) of linear magnetic material (permeability μ). Show that the magnetic field inside the sphere (0 < r ≤ R) is / What is the field outside the sphere?
> At the interface between one linear magnetic material and another, the magnetic field lines bend (Fig. 6.32). Show that tan θ2/ tan θ1 μ2/μ1, assuming there is no free current at the
> Compare Eqs. 2.15, 4.9, and 6.11. Notice that if ρ, P, and M are uniform, the same integral is involved in all three: Therefore, if you happen to know the electric field of a uniformly charged object, you can immediately write d
> Notice the following parallel: Thus, the transcription turns an electrostatic problem into an analogous magnetostatic one. Use this, together with your knowledge of the electrostatic results, to rederive (a) the magnetic field inside a uni
> Imagine two charged magnetic dipoles (charge q, dipole moment m), constrained to move on the z axis (same as Problem 6.23(a), but without gravity). Electrically they repel, but magnetically (if both m’s point in the z direction) they attract. (a) Find th
> A familiar toy consists of donut-shaped permanent magnets (magnetization parallel to the axis), which slide frictionlessly on a vertical rod (Fig. 6.31). Treat the magnets as dipoles, with mass md and dipole moment m. (a) If you put two back-to-back magn
> In Prob. 6.4, you calculated the force on a dipole by “brute force.” Here’s a more elegant approach. First write B(r) as a Taylor expansion about the center of the loop: where r0 is the position of th
> (a) Show that the energy of a magnetic dipole in a magnetic field B is [Assume that the magnitude of the dipole moment is fixed, and all you have to do is move it into place and rotate it into its final orient
> How would you go about demagnetizing a permanent magnet (such as the wrench we have been discussing, at point c in the hysteresis loop)? That is, how could you restore it to its original state, with M = 0 at I = 0?
> Starting from the Lorentz force law, in the form of Eq. 5.16, show that the torque on any steady current distribution (not just a square loop) in a uniform field B is m × B.
> Calculate the surface integral of the function in Ex. 1.7, over the bot- tom of the box. For consistency, let “upward” be the positive direction. Does the surface integral depend only on the boundary line for this function? What is the total flux over the

