Question: The price sensitivity hedge ratio, including yield
The price sensitivity hedge ratio, including yield beta, was shown in this chapter to be
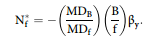
Discuss how changing each of the five input parameters will influence the hedge ratio (assume that all input parameters are positive).
Transcribed Image Text:
MDB MD B' N; : By-
> Using the information in the previous problem, calculate the price of the put described in problem 17, using the Black model for pricing puts.
> Use the Black model to determine a fair price for an interest rate put that expires in 74 days. The forward rate is 9.79 percent, and the exercise rate is 10 percent. The appropriate risk-free rate is 8.38 percent. All rates are continuously compounded.
> Assume the 30-day LIBOR is 5 percent and the 120-day LIBOR is 6 percent. This implies a continuously compounded 90-day forward rate of 6.3448 percent. Verify this result and explain what happens to the continuously compounded forward rate as the number o
> Assume the 30-day LIBOR is 5 percent and the 120-day LIBOR is also 5 percent. This implies a continuously compounded 90-day forward rate of 5.0172 percent. Verify this result and explain what happens to the continuously compounded 90-day forward rate as
> A bank is offering an interest rate call with an expiration of 45 days. The call pays off based on 180-day LIBOR. The volatility of forward rates is 17 percent. The 45-day forward rate for 180-day LIBOR is 0.1322, and the exercise rate is 12 percent. The
> Identify and define three versions of put-call parity.
> In each case examined in this chapter and in the preceding problems, we did not account for the interest on funds invested. One useful way to observe the effect of interest is to look at a conversion or a reverse conversion. Evaluate the August 165 puts
> You are the manager of a bond portfolio of $10 million face value of bonds worth $9,448,456. The portfolio has a yield of 12.25 percent and a duration of 8.33. You plan to liquidate the portfolio in six months and are concerned about an increase in inter
> Assume a standard deviation of 8 percent and use the Black model to determine whether the call option in problem 17 is correctly priced. If not, suggest a riskless hedge strategy.
> Consider a $30 million notional amount interest rate swap with a fixed rate of 7 percent, paid quarterly on the basis of 90 days in the quarter and 360 days in the year. The first floating payment is set at 7.2 percent. Calculate the first net payment an
> On March 16, the June Treasury bond futures contract was priced at 100 17/32 and the September contract was at 99 17/32. Determine the implied repo rate on the spread. Assume that the cheapest bond to deliver on both contracts is the 11 1/4 maturing in 2
> Complete the following table with the correct formula related to various spread strategies. Collar Strategies Straddle with Calls with Calls Item and Puts and Puts Value at expiration Profit Maximum profit Maximum loss Breakeven and
> Complete the following table with the correct formula related to various spread strategies. Bull Вear Butterfly Spread Spread Spread Item with Calls with Puts with Calls Value at еxpiration Profit Maximum profit Maximum loss Breakeven and
> Suppose there is a commodity in which the expected future spot price is $60. To induce investors to buy futures contracts, a risk premium of $4 is required. To store the commodity for the life of the futures contract would cost $5.50. Find the futures pr
> Examine the following pairs of puts, which differ only by exercise price. Determine whether either of them violates the rules regarding relationships between American options that differ only by exercise price. a. August 155 and 160 b. October 160 and
> Examine the following pairs of calls, which differ only by exercise price. Determine whether either of them violates the rules regarding relationships between American options that differ only by exercise price. a. August 155 and 160 b. October 160 and
> Repeat the last problem using the approximation for an at-the-money call. Compare your answer with the one you obtained in problem 13. Is the approximation a good one? Why or why not?
> A swap dealer quotes that the rate on a plain vanilla swap, for it to pay fixed, is the five-year Treasury rate plus 10. To receive fixed, the dealer quotes the rate as the five-year Treasury rate plus 15. Assuming the five-year Treasury rate is 7.60 per
> Construct a table containing the up and down factors for a one-year option with a stock volatility of 55 percent and a risk-free rate of 7 percent for n 1, 5, 10, 50, and 100, where n is the number of binomial periods. Let u and d be defined as = e°V
> Consider a $100 million equity swap with semiannual payments. When the swap is established, the underlying stock is at 1,215.52. One party pays a fixed rate of 5.5 percent based on the assumption of 30 days per month and 360 days in a year. If the stock
> Solve for the price of a forward contract on a generic asset that expires on September 10 whose spot price as of June 10 is $45, assuming that the annually compounded risk-free rate is 6.01 percent.
> A corporation enters into a $35 million notional amount interest rate swap. The swap calls for the corporation to pay a fixed rate and receive a floating rate of LIBOR. The payments will be made every 90 days for one year and will be based on the adjustm
> The CEO of a large corporation holds a position of 25 million shares in her company’s stock, which is currently priced at $20 and pays no dividends. She is concerned that because of her large shareholdings and the fact that her compensation is tied to th
> The U.K. manager of an international bond portfolio would like to synthetically sell a large position in a French government bond, denominated in euros. The bond is selling at its par value of €46.15 million, which is equivalent to £30 million at the cur
> Suppose you are a municipal finance director for a large metropolitan city. Based on your asset-liability analysis, you determine that your rate-sensitive assets are equivalent to a one-year LIBOR deposit and your rate-sensitive liabilities are equivalen
> Suppose a trader has entered two $15 million notional amount equity swaps both with a fixed rate of 6 percent, paid quarterly on the basis of 90 days in the quarter and 360 days in the year. The first swap is a receive fixed and pay three-month total ret
> Suppose a trader has entered two $50 million notional amount interest rate swaps both with a fixed rate of 3 percent, paid quarterly on the basis of 90 days in the quarter and 360 days in the year. The first swap is a receive fixed and pay three-month LI
> An interest rate swap has two primary risks associated with it. Identify and explain each risk.
> On January 31, a firm learns that it will have additional funds available on May 31. It will use the funds to purchase $5,000,000 par value of the APCO 9 1/2 percent bonds maturing in about 21 years. Interest is paid semiannually on March 1 and September
> On January 2 of a particular year, an American firm decided to close out its account at a Canadian bank on February 28. The firm is expected to have 5 million Canadian dollars in the account at the time of the withdrawal. It would convert the funds to U.
> On June 17 of a particular year, an American watch dealer decided to import 100,000 Swiss watches. Each watch costs SF225. The dealer would like to hedge against a change in the dollar/Swiss franc exchange rate. The forward rate was $0.3881. Determine th
> Use the information in problem 16 to construct a euro covered call. Assume that the spot rate at the start is $0.9825.
> On March 16, the March Treasury bond futures settlement price was 101 21/32. Assume that the 12 1/2 percent bond maturing in about 22 years is the cheapest bond to deliver. The CF is 1.4639. Assume that the price at 3:00 P.M. was 150 15/32. Determine the
> For each of the following situations, determine whether a long or short hedge is appropriate. Justify your answers. a. A firm anticipates issuing stock in three months. b. An investor plans to buy a bond in 30 days. c. A firm plan to sell some foreign
> Explain how to determine whether to buy or sell futures when hedging.
> a. Define the minimum variance hedge ratio and the measure of hedging effectiveness. What do these two values tell you? b. What is the price sensitivity hedge ratio? How are the price sensitivity and minimum variance hedge ratios alike? How are they di
> Suppose you are a dealer in sugar. It is September 26, and you hold 112,000 pounds of sugar worth $0.0479 per pound. The price of a futures contract expiring in January is $0.0550 per pound. Each contract is for 112,000 pounds. a. Determine the original
> Recall from the chapters on options that we learned about bull and bear spreads. Intermarket futures spreads also are considered bull and bear spreads. Describe what you think might be a bull spread with T-bonds futures. Be sure to explain your reasoning
> You plan to buy 1,000 shares of Swiss International Airlines stock. The current price is SF950. The current exchange rate is $0.7254/SF. You are interested in speculating on the stock but do not want to assume any currency risk. You plan to hold the posi
> As we discussed in the chapter, futures can be used to eliminate systematic risk in a stock portfolio, leaving it essentially a risk-free portfolio. A portfolio manager can achieve the same result, however, by selling the stocks and replacing them with T
> The manager of a $20 million portfolio of domestic stocks with a beta of 1.10 would like to begin diversifying internationally. He would like to sell $5 million of domestic stock and purchase $5 million of foreign stock. He learns that he can do this usi
> Explain how the implied repo rate on a spread transaction differs from that on a nearby futures contract.
> A euro put with an exercise price of $1.00 is priced at $0.0435. Construct a simple long position in the put.
> You are the manager of a stock portfolio worth $10,500,000. It has a beta of 1.15. During the next three months, you expect a correction in the market that will take the market down about 5 percent; thus, your portfolio is expected to fall about 5.75 per
> On August 20, a stock index future, which expires on September 20, was priced at 429.70. The index was at 428.51. The dividend yield was 2.7 percent. Discuss the concept of the implied repo rate on an index arbitrage trade. Determine the implied repo rat
> On November 1, an analyst who has been studying a firm called Computer Sciences believes that the company will make a major announcement before the end of the year. Computer Sciences currently is priced at 27.63 and has a beta of 0.95. The analyst believ
> During the first six months of the year, yields on long-term government debt have fallen about 100 basis points. You believe that the decline in rates is over, and you are interested in speculating on a rise in rates. You are, however, unwilling to assum
> On March 1, a securities analyst recommended General Cinema stock as a good purchase in the early summer. The portfolio manager plans to buy 20,000 shares of the stock on June 1 but is concerned that the market as a whole will be bullish over the next th
> You are the manager of a stock portfolio. On October 1, your holdings consist of the eight stocks listed in the following table, which you intend to sell on December 31. You are concerned about a market decline over the next three months. The number of s
> Based on the jet fuel exposure information in the previous problem, calculate the hedging effectiveness. Explain how to interpret this number.
> Suppose you are concerned about your firm’s jet fuel exposure. Further, your analysis suggests the best futures contract to hedge jet fuel is unleaded gasoline. The fuel volatility (standard deviation of changes in your firm’s entire jet fuel exposure) i
> On July 1, a portfolio manager holds $1 million face value of Treasury bonds, the 11 l/4s maturing in about 29 years. The price is 107 14/32. The bond will need to be sold on August 30. The manager is concerned about rising interest rates and believes th
> A call option on the euro expiring in six months has an exercise price of $1.00 and is priced at $0.0385. Construct a simple long position in the call.
> A major bread maker is planning to purchase wheat in the near future. Identify and explain the appropriate hedging strategy.
> Assume that there is a forward market for a commodity. The forward price of the commodity is $45. The contract expires in one year. The risk-free rate is 10 percent. Now six months later, the spot price is $52. What is the forward contract worth at this
> Rework the last problem assuming that the index was at 388.14 at expiration. Determine the profit from the arbitrage trade and express it in terms of the profit from the spot and futures sides of the transaction. How does your answer relate to that in pr
> Explain why the Black option on futures pricing model is simply a pricing model for options on instruments with a zero cost of carry.
> Explain why American call options on futures could be exercised early when call options on the spot are not. Assume that there are no dividends.
> On July 10, a farmer observes that the spot price of corn is $2.735 per bushel and the September futures price is $2.76. The farmer would like a prediction of the spot price in September but believes the market is dominated by hedgers holding long positi
> Calculate the net effect that a change in the annually compounded risk-free rate from 6.83 percent to 6.60 percent would make on the price of a commodity futures contract whose spot price as of March 30 was $49.90, assuming that there is a $5.60 storage
> Suppose that a futures margin account pays interest but at a rate that is less than the risk-free rate. Consider a trader who buys the asset and sells a future to form a risk-free hedge. Would the trader believe that the futures price should be lower or
> Suppose there is a futures contract on a portfolio of stocks that currently are worth $100. The futures have a life of 90 days, and during that time, the stocks will pay dividends of $0.75 in 30 days, $0.85 in 60 days, and $0.90 in 90 days. The simple in
> Using the Black–Scholes–Merton option pricing model and the generic carry formula for forward contracts (using continuous compounding), demonstrate that Ce S0,T,X Ce f 0 T ,T,X .
> Buy 100 shares of stock and buy one August 165 put contract. Hold the position until expiration. Determine the profits and graph the results. Determine the breakeven stock price at expiration, the maximum profit, and the maximum loss. For problems 16, 17
> Suppose you observe a one-year futures price of $100, the futures option strike price of $90, and a 5 percent interest rate (annual compounding). If the futures option call price is quoted at $9.40, identify any arbitrage and explain how it would be capt
> Suppose the U.S. interest rate for the next six months is 1.5 percent (annual compounding). The foreign interest rate is 2 percent (annual compounding). The spot price of the foreign currency in dollars is $1,665. The forward price is $1,664. Determine t
> Given an investor holding a long position two days prior to expiration, when will he prefer futures contracts to forward contracts? (Do not assume interest rate certainty.)
> On July 5, a stock index futures contract was at 394.85. The index was at 392.54, the risk-free rate was 2.83 percent, the dividend yield was 2.08 percent, and the contract expired on September 20. Determine whether an arbitrage opportunity was available
> The put–call parity rule can be expressed as C P f 0 T X 1 r T. Consider the following data: f 0 T 102, X 100, r 0 1, T 0 25, C 4, and P 1 75. A few calculations will show that the prices do not conform to the rule. Suggest an arbitrage strategy and show
> Use the following data from January 31 of a particular year for a group of March 480 options on futures contracts to answer parts a through g. Futures price: 483.10 Expiration: March 13 Risk-free rate: 0.0284 percent (simple) Call price: 6.95 Put price:
> On September 12, a stock index futures contract was at 423.70. The December 400 call was at 26.25, and the put was at 3.25. The index was at 420.55. The futures and options expire on December 21. The discrete risk-free rate was 2.75 percent. Determine wh
> The following information was available: spot rate for Japanese yen: $0.009313; 730-day forward rate for Japanese yen: $0.010475 (assume a 365-day year); U.S. risk-free rate: 7.0 percent; Japanese risk-free rate: 1.0 percent a. Assuming annual compoundi
> On a particular day, the September S&P 500 stock index futures was priced at 960.50. The S&P 500 index was at 956.49. The contract expires 73 days later. a. Assuming continuous compounding, suppose the risk-free rate is 5.96 percent and the dividend yie
> On September 26, the spot price of wheat was $3.5225 per bushel and the price of a December wheat futures was $3.64 per bushel. The interest forgone on money tied up in a bushel until expiration is 0.03, and the cost of storing the wheat is 0.0875 per bu
> Repeat the previous problem, but close the position on September 1. Use the spreadsheet to find the profits for the possible stock prices on September 1. Generate a graph and use it to approximate the breakeven stock price.
> Construct an arbitrage example involving an asset that can be sold short and use it to explain the cost of carry model for pricing futures.
> On a particular day, the S&P 500 futures settlement price was 899.30. You buy one contract at the settlement price at around the close of the market. The next day the contract opens at 899.70, and the settlement price at the close of the day is 899.10. D
> Suppose you are expecting the stock price to move substantially over the next three months. You are considering a butterfly spread. Construct an appropriate butterfly spread using the October 160, 165, and 170 calls. Hold the position until expiration. D
> Construct a collar using the October 160 put. First, use the Black–Scholes–Merton model to identify a call that will make the collar have zero up-front cost. Then close the position on September 20. Use the spreadsheet to find the profits for the possibl
> Assume that on March 16, the cheapest bond to deliver on the June Treasury bond futures contract is the 14s, callable in about 19 years and maturing in about 24 years. Coupons are paid on November 15 and May 15. The price of the bond is 161 23/32, and th
> Repeat problem 6, but close the position on September 20. Use the spreadsheet to find the profits for the possible stock prices on September 20. Generate a graph and use it to identify the approximate breakeven stock price.
> Construct a bear money spread using the October 165 and 170 calls. Hold the position until the options expire. Determine the profits and graph the results. Identify the breakeven stock price at expiration and the maximum and minimum profits. Discuss any
> The chapter showed how analyzing a box spread is like a capital budgeting problem using the NPV approach. Consider the internal rate of return method of examining capital budgeting problems and analyze the box spread in that context.
> Many option traders use a combination of a money spread and a calendar spread called a diagonal spread. This transaction involves the purchase of a call with a lower exercise price and longer time to expiration and the sale of a call with a higher exerci
> Another variation of the straddle is called a strangle. A strangle is the purchase of a call with a higher exercise price and a put with a lower exercise price. Evaluate the strangle strategy by examining the purchase of the August 165 put and 170 call.
> Buy 100 shares of stock and write one October 170 call contract. Hold the position until expiration. Determine the profits and graph the results. Identify the breakeven stock price at expiration, the maximum profit, and the maximum loss.
> Pear, Inc. is presently trading at $100 per share; at-the-money one-month calls are trading at $5.43, and puts are trading at $5.01; and at the-money two-month calls are trading at $7.72, and puts are trading at $6.89. At present, these option prices ref
> Explain conceptually the choice of strike prices when it comes to designing a zero-cost collar. Specifically, address the costs and benefits of two strategies. One strategy has a higher put strike price than the second strategy.
> Explain conceptually the choice of strike prices when it comes to designing a call-based bull spread. Specifically, address the costs and benefits of two bull spread strategies. One strategy has the call strike prices further from the current stock price
> Explain why a straddle is not necessarily a good strategy when the underlying event is well known to everyone.
> Analyze the August 160/170 box spread. Determine whether a profit opportunity exists. If it does, explain how to exploit it.
> It is August 20, and you are trying to determine which of two bonds is the cheaper bond to deliver on the December Treasury bond futures contract. The futures price is 89 12/32. Assume that delivery will be made on December 14 and use 7.9 percent as the
> A strip is a variation of a straddle involving two puts and one call. Construct a short strip using the August 170 options. Hold the position until the options expire. Determine the profits and graph the results. Identify the breakeven stock prices at ex
> A slight variation of a straddle is a strap, which uses two calls and one put. Construct a long strap using the October 165 options. Hold the position until expiration. Determine the profits and graph the results. Identify the breakeven stock prices at e
> Identify and discuss four nontraded delivery options related to U.S. Treasury bond futures contracts.
> Buy one August 165 call contract. Hold it until the options expire. Determine the profits and graph the results. Then identify the breakeven stock price at expiration. What is the maximum possible loss on this transaction?
> Buying an at-the-money put has a greater return potential than buying an out-of-the-money put because it is more likely to be in-the-money. Appraise this statement.
> Suppose the stock pays a $1.10 dividend with an ex-dividend date of September 10. Rework part of problem 7 using an appropriate dividend adjusted procedure. Calculate this answer by hand and then recalculate it using BlackScholesMertonBinomial10e.xlsm.
> Use the Black–Scholes–Merton European put option pricing formula for the October 165 put option. Repeat parts a, b, and c of the previous problem with respect to the put.
> Let the standard deviation of the continuously compounded return on the stock is 21 percent. Ignore dividends. Respond to the following: a. What is the theoretical fair value of the October 165 call? Calculate this answer by hand and then recalculate it

