Question: The Riemann zeta-function / is defined by /
The Riemann zeta-function / is defined by
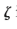
and is used in number theory to study the distribution of prime numbers. What is the domain of /?
Transcribed Image Text:
> Use the substitution u = 1/x to show that
> We can extend our definition of average value of a continuous function to an infinite interval by defining the average value off on the interval / (a) Find the average value of y = tan-1 x on the interval / (b) If / is divergent, show that the average va
> Determine whether the sequence converges or diverges. If it converges, find the limit.
> Use series to approximate the definite integral to within the indicated accuracy. "x'arctan x dx (four decimal places)
> Find the area of the region bounded by the curves y = 1/(2 + Jx), y = 1/(2 – Jx), and x = 1.
> Determine whether the series is convergent or divergent. Σ n-1 n
> (a) Use the reduction formula in Example 6 to show that where n > 2 is an integer. (b) Use part (a) to evaluate (c) Use part (a) to show that, for odd powers of sine, w/2 sin"x dx n - п — 1 w/2 sin" 2x dx Jo Sa/? sin'x dx and " sin'x dx. 2·4· 6 ·
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 3 Σ 5" n
> Find the area of the region bounded by the hyperbola y2 - x2 = 1 and the line y = 3.
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2 + sin x - dx 1 (b) dx V1 + x4 (a)
> Determine whether the sequence converges or diverges. If it converges, find the limit. an cos n + 1
> Suppose you are asked to estimate the volume of a football. You measure and find that a football is 28 cm long. You use a piece of string and measure the circumference at its widest point to be 53 cm. The circumference 7 cm from each end is 45Â&nbs
> A population of honeybees increased at a rate of r(t) bees per week, where the graph of r is as shown. Use Simpson’s Rule with six subintervals to estimate the increase in the bee population during the first 24 weeks. 12000 8000 40
> The speedometer reading (v) on a car was observed at 1-minute intervals and recorded in the chart. Use Simpson’s Rule to estimate the distance traveled by the car. I (min) v (mi/h) 1 (min) v (mi/h) 40 56 1 42 7 57 2 45 8 57 3 49 9
> Evaluate the integral. x - 1 x² + 2x
> Evaluate the indefinite integral as an infinite series. S arctan(x²) dx
> If a surveyor measures differences in elevation when making plans for a highway across a desert, corrections must be made for the curvature of the earth. (a) If R is the radius of the earth and L is the length of the highway, show that the correction is
> Estimate the errors involved in Exercise 63, parts (a) and (b). How large should n be in each case to guarantee an error of less than 0.00001? Data from Exercise 63: (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s R
> Test the series for convergence or divergence. 2n TT E (-1)*. (2n)!
> (a) Prove the reduction formula (b) Use part (a) to evaluate (c) Use parts (a) and (b) to evaluate | cos"x dx 1 cos" 'x sin x + п — 1 | cos" ?x dx n ſ cos?x dx. S cos*x dx.
> Determine whether the sequence converges or diverges. If it converges, find the limit. 4" а, 1+ 9"
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its Σ TT
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 10 – 2 + 0.4 – 0.08 + ·
> (a) Explain the difference between (b) Explain the difference between a and ミ E ai E a; and i-1
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> (a) Find the highest and lowest points on the curve x4 + y4 = x2 + y2. (b) Sketch the curve. (Notice that it is symmetric with respect to both axes and both of the lines y = ±x, so it suffices to consider y > x > 0 initially.) (c) Use polar coordinates a
> Test the series for convergence or divergence. n' (1 + n)"
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(a) — хе 2", а — 0 ()
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain
> Calculate the first eight terms of the sequence of partial sums correct to four decimal places. Does it appear that the series is convergent or divergent? (-1)* "-| n!
> Calculate the first eight terms of the sequence of partial sums correct to four decimal places. Does it appear that the series is convergent or divergent? Σ sinn R-1
> Calculate the first eight terms of the sequence of partial sums correct to four decimal places. Does it appear that the series is convergent or divergent?
> Calculate the first eight terms of the sequence of partial sums correct to four decimal places. Does it appear that the series is convergent or divergent? 1 Σ i n* + n?
> Use a calculator to find the length of the curve correct to four decimal places. If necessary, graph the curve to determine the parameter interval. r = tan 0, 7/6 < 0 < T/3
> he outer circle in the figure has radius 1 and the centers of the interior circular arcs lie on the outer circle. Find the area of the shaded region.
> (a) What is the difference between a sequence and a series? (b) What is a convergent series? What is a divergent series?
> Find all values of c for which the following series converges. n + 1
> Determine whether the series is absolutely convergent or conditionally convergent. sin n 2" n-1
> (a) Use (4) to show that if sn is the nth partial sum of the harmonic series, then (b) The harmonic series diverges, but very slowly. Use part (a) to show that the sum of the first million terms is less than 15 and the sum of the first billion terms is l
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L.2' dr
> (a) Use a computer algebra system to evaluate the following integrals. (b) Based on the pattern of your responses in part (a), guess the value of / Then use your CAS to check your guess. (c) Based on the patterns in parts (a) and (b), make a conjecture a
> (a) Use the sum of the first 10 terms to estimate the sum of the series / How good is this estimate? (b) Improve this estimate using (3) with n = 10. (c) Compare your estimate in part (b) with the exact value given in Exercise 34. (d) Find a value of n t
> Euler also found the sum of the p-series with p = 4: Use Euler’s result to find the sum of the series. IT 3(4) = E n° 90 (a) 2 1 (b) E (k – 2)4 8
> Test the series for convergence or divergence. n? – 1 E (-1)". n2 + 1
> Leonhard Euler was able to calculate the exact sum of the p-series with p = 2: Use this fact to find the sum of each series. 2 IT 3(2) = Σ 6. (a) Σ 1 (b) Σ R-2 n (n + 1)? n-3 1 (c) Σ (2n)?
> Find the values of p for which the series is convergent. In n Σ n-1
> Find the values of p for which the series is convergent. E n(1 + n²)"
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. Sp dp 12
> Find the values of p for which the series is convergent. 1 Σ n In n [In(In n)]P
> Find the values of p for which the series is convergent. 1 Σ n(In n)" -2
> (a) Use a computer algebra system to evaluate the following integrals. (b) Based on the pattern of your responses in part (a), guess the value of (c) Use integration by parts to prove the conjecture that you made in part (b). For what values of n is it v
> Explain why the Integral Test can’t be used to determine whether the series is convergent. CS TN R-1
> Determine whether the series is convergent or divergent. Σ n-1 n* + 1
> Determine whether the series is convergent or divergent. 1 Σ n2 + 3 n-
> Determine whether the series is convergent or divergent. E ke * k-1
> Test the series for convergence or divergence. 2(-1)- n² – 1 n + 1 E(-1) - R-1
> Determine whether the series is convergent or divergent. ke k-1
> Determine whether the series is convergent or divergent. In n -2 n
> Use a Maclaurin series to obtain the Maclaurin series for the given function. f(x) = x² In(1 + x')
> Determine whether the series is convergent or divergent. 1 n-2 n In n
> Determine whether the series is convergent or divergent. Зп — 4 Σ R-3 n 2n
> Determine whether the series is convergent or divergent. 3. Σ -1 n* + 4
> (a) Use a computer algebra system to evaluate the following integrals. (b) Based on the pattern of your responses in part (a), guess the value of the integral (c) Check your guess with a CAS. Then prove it using the techniques of Section 7.2. For what va
> Determine whether the series is convergent or divergent. 1 -1 n? + 2n + 2
> Determine whether the series is convergent or divergent. 1 n2 + 4 8
> Determine whether the series is convergent or divergent. 1 + n³/2
> Determine whether the series is convergent or divergent. Vn + 4 n° ,2
> Determine whether the series is convergent or divergent. 1 + 2/2 1 + 4/4 1 + 3/3 5/5
> Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. S(x) — sin x, a — п/6
> Determine whether the series is convergent or divergent. 1 1 3 11 15 19
> Determine whether the series is convergent or divergent. 11 13
> Determine whether the series is convergent or divergent. Σ 0.9999 n-3
> Use the Integral Test to determine whether the series is convergent or divergent. E n’e * R-1
> (a) Use a computer algebra system to evaluate the following integrals. (b) Based on the pattern of your responses in part (a), guess the value of the integral if a ≠b. What if a = b? (c) Check your guess by asking your CAS to evaluate
> Use the Integral Test to determine whether the series is convergent or divergent. Σ A n² + 1
> Use the Integral Test to determine whether the series is convergent or divergent. 1 Σ (Зл — 1)*
> Use the Integral Test to determine whether the series is convergent or divergent. 2 Σ 5n – 1 ー1
> Use the Integral Test to determine whether the series is convergent or divergent. En 0.3 R-1 8
> Use the Integral Test to determine whether the series is convergent or divergent. En R-1
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 · dx (2х + 1)°
> Suppose f is a continuous positive decreasing function for x > 1 and an = f (n). By drawing a picture, rank the following three quantities in increasing order: 5 E ai E ai i-2 i-I
> Draw a picture to show that What can you conclude about the series? 1 Σ 1.3 -2 n 1.3
> For values of k between 3.6 and 4, compute and plot at least 100 terms and comment on the behavior of the sequence. What happens if you change p0 by 0.001? This type of behavior is called chaotic and is exhibited by insect populations under certain condi
> Evaluate the integral. tan 2y dy
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 3 — 4х 00
> (a) Show that the function defined by is not equal to its Maclaurin series. (b) Graph the function in part (a) and comment on its behavior near the origin. 1/22 if x + 0 f(x) = if x- 0
> The meaning of the decimal representation of a number 0.d1d2d3 ... (where the digit di is one of the numbers 0, 1, 2, . . . , 9) is that Show that this series always converges. di 0.d,d;dzd4 . .. 10 dz dz d4 102 103 104
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. 1 -1 3" + 4"
> Experiment with values of k between 3.4 and 3.5. What happens to the terms?
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. E 5 "cos’n cos'n 2.
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. 1/m nº
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x(2 – y) II yA --
> Determine whether the sequence converges or diverges. If it converges, find the limit. tan 'n an n
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. 1 5 + n*
> Determine whether the series converges or diverges. Σ 1+1/m
> Determine whether the series converges or diverges. Σ sin

