Question: The scores below are a modification of
The scores below are a modification of the scores in Problem 6:
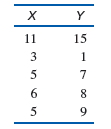
a. Compute SS for X and Y and SP. Compare these values to your answer for part a of Problem 6.
b. Compute the Pearson correlation. Compare your results to what you got for part b of Problem 6.
Problem 6:
> For random samples of size n = 16 selected from a normal distribution with a mean of μ = 75 and a standard deviation of σ = 20, find each of the following: a. The range of sample means that defines the middle 95% of the distribution of sample means. b. T
> Use summation notation to express each of the following calculations: a. Add the scores and then square the sum. b. Square each score and then add the squared values. c. Subtract 2 points from each score and then add the resulting values. d. Subtract 1 p
> Briefly define each of the following: a. Distribution of sample means b. Central limit theorem c. Expected value of M d. Standard error of M
> A report in 2016 indicates that Americans between the ages of 8 and 18 spend an average of μ = 10 hours per day using some sort of electronic device such as a smartphone computer, or tablet. Assume that the distribution of times is normal with a standard
> Define sampling with replacement and explain why it is used.
> On an exam with a mean of M = 40, you obtain a score of X = 35. a. Relative to other students, would your performance on the exam be better with a standard deviation of s = 2 or with a standard deviation of s = 8? (Hint: Sketch each distribution and find
> An important reason that students struggle in college is that they are sometimes unaware that they have not yet mastered a new skill. Struggling students often overestimate their level of mastery in part because the skills needed to master a topic are th
> IQ test scores are standardized to produce a normal distribution with a mean of μ = 100 and a standard deviation of σ = 15. Find the proportion of the population in each of the following IQ categories. a. Genius or near genius: IQ over 140 b. Very superi
> A normal distribution has a mean of m 5 70 and a standard deviation of s 5 12. For each of the following scores, indicate whether the body is to the right or left of the score and find the proportion of the distribution located in the body. a. X = 74 b.
> A normal distribution has a mean of m = 50 and a standard deviation of s = 5. For each of the following scores, indicate whether the tail is to the right or left of the score and find the proportion of the distribution located in the tail. a. X = 45 b. X
> The range is completely determined by the two extreme scores in a distribution. The standard deviation, on the other hand, uses every score. a. Compute the range (choose either definition), the variance, and the standard deviation for the following sampl
> A population with a mean of μ = 41 and a standard deviation of σ = 4 is transformed into a standardized distribution with μ = 100 and σ = 20. Find the new, standardized score for each of the following values from the original population. a. X = 39 b. X =
> Use summation notation to express the following calculations. a. Multiply scores X and Y and then add each product. b. Sum the scores X and sum the scores Y and then multiply the sums. c. Subtract X from Y and sum the differences. d. Sum the X scores.
> For each of the following, identify the exam score that should lead to the better grade. In each case, explain your answer. a. A score of X = 70 on an exam with μ = 82 and σ 5 8; or a score of X = 60 on an exam with μ = 72 and σ = 12. b. A score of X = 5
> In a sample distribution, a score of X = 21 corresponds to z = -1.00 and a score of X = 12 corresponds to z = -2.50. Find the mean and standard deviation for the sample.
> Solve the following problems. a. After 6 points have been added to every score in a sample, the mean is found to be M = 70 and the standard deviation is s = 13. What were the values for the mean and standard deviation for the original sample? b. After ev
> Calculate SS, σ2, and σ for the following population of N = 4 scores: 0, 6, 6, 8.
> For the following population of scores: 1, 4, 7 a. Calculate the population mean and population variance. b. Complete the following table that lists all possible samples of n = 2 scores from the population. Use the first three rows (Samples aâ€
> For the following sample of n = 10 scores, 6, 5, 4, 3, 3, 3, 2, 2, 2, 1 a. Assume that the scores are measurements of a discrete variable and find the median. b. Assume that the scores are measurements of a continuous variable and find the precise median
> For the following scores, find the value of each expression:
> For a sample of n = 12 scores, what value should be used in the denominator of the formula for variance? What value should be used in the denominator of the formula for the mean? Explain why the two formulas use different values in the denominator.
> Doebel and Munakata (2018) discovered that delay of gratification by children is influenced by social context. All children were told that they were in the “green group” and were placed in a room with a single marshmallow. Participants were told that the
> Dwyer, Figuerooa, Gasalla, and Lopez (2018) showed that learning of flavor preferences depends on the relative value of the reward with which a flavor is paired. In their experiment, rats received pairings of a cherry flavor with 8% sucrose solution afte
> For the following set of scores, find the value of each expression:
> Ackerman and Goldsmith (2011) compared learning performance for students who studied material printed on paper versus students who studied the same material presented on a computer screen. All students were then given a test on the material and the resea
> A survey given to a sample of college students contained questions about the following variables. For each variable, identify the kind of graph that should be used to display the distribution of scores (histogram, polygon, or bar graph). a. Age b. Birth-
> Deters and Mehl (2013) studied the effect of Facebook status updates on feelings of loneliness. Eighty-six participants were randomly assigned to two groups. One group was instructed to post more social media status updates and the other group was not. T
> Calculate the mean for both of the following sets of scores. Use both the computational and definitional formulas to compute SS for both sets of scores. Round to two decimal places for each calculation. Why is there a difference in the calculated SS for
> The results of a recent study showed that children who routinely drank reduced fat milk (1% or skim) were more likely to be overweight or obese at ages 2 and 4 compared to children who drank whole or 2% milk (Scharf, Demmer, & DeBoer, 2013). a. Is this a
> There are two different formulas or methods that can be used to calculate SS. a. Under what circumstances is the definitional formula easy to use? b. Under what circumstances is the computational formula preferred?
> One sample has a mean of M = 6, and a second sample has a mean of M = 12. The two samples are combined into a single set of scores. a. What is the mean for the combined set if both the original samples have n = 4 scores? b. What is the mean for the combi
> Your friend measures the temperature of her coffee to be 70° Celsius. Your friend also notices that the temperature outside is 35° Celsius. Why is it incorrect to say that the coffee is twice as warm as the temperature outside?
> Four scales of measurement were introduced in this chapter, from simple classification on a nominal scale to the more informative measurements from a ratio scale. a. What additional information is obtained from measurements on an ordinal scale compared t
> In a sample of n = 6 scores, five of the scores are each above the mean by one point. Where is the sixth score located relative to the mean?
> Two scores, X and Y, are recorded for each of n 5 5 participants. For these scores, find the value of each expression.
> A tax form asks people to identify their age, annual income, number of dependents, and social security number. For each of these four variables, identify the scale of measurement that probably is used and identify whether the variable is continuous or di
> Explain why honesty is a hypothetical construct instead of a concrete variable. Describe how honesty might be measured and defined using an operational definition.
> A professor is interested in whether student performance on exams is better in the afternoon than in the morning. One sample of students was randomly assigned to receive the exam in the morning and another sample was randomly assigned to receive the exam
> For the following set of scores: a. Construct a frequency distribution table to organize the scores. Include cumulative frequency and cumulative percent. b. What is the percentile rank of the upper real limit of X = 15? c. What is the upper real limit of
> For each of the following, calculate the pooled variance and the estimated standard error for the sample mean difference a. The first sample has n = 4 scores and a variance of s2 = 17, and the second sample has n = 8 scores and a variance of s2 = 27. b.
> In Problem 8, a researcher asked college students to evaluate three new smartphone designs. However, the researcher suspects that college students may have criteria that are different from those used by older adults. To test this hypothesis, the research
> Research indicates that people who volunteer to participate in research studies tend to have higher intelligence than nonvolunteers. To test this phenomenon, a researcher obtains a sample of 200 high school students. The students are given a description
> Suppose that a researcher is interested in differences between young adults and older adults with respect to social media preferences. The researcher asked participants to indicate their preference for a specific social media application by checking all
> Many businesses use some type of customer loyalty program to encourage repeat customers. A common example is the buy-ten-get-one-free punch card. Drèze and Nunes (2006) examined a simple variation of this program that appears to give customer
> Liu et al. (2015) recently reported the results of a study examining whether happy people live longer. The study followed a large sample of British women, aged 50 to 69 over a 10-year period. At the beginning of the study the women were asked several que
> For the following set of scores, find the value of each expression:
> Earlier in the chapter, we introduced the chi-square test of independence with a study examining the relationship between personality and color preference. The following table shows the frequency distribution for a group of n = 200 students who were clas
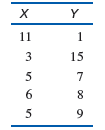
> With a small sample, a single point can have a large effect on the magnitude of the correlation. To create the following data, we started with the scores from Problem 8 and changed the first X value from X = 3 to X = 8. a. Sketch a scatter plot and estim
> For the following scores, a. Sketch a scatter plot and estimate the value of the Pearson correlation. b. Compute the Pearson correlation.
> For the following scores, a. Compute SS for X and Y and SP. b. Compute the Pearson correlation.
> For the following scores, a. Sketch a scatter plot and estimate the Pearson correlation. b. Compute the Pearson correlation.
> For the following scores, a. Sketch a scatter plot and estimate the Pearson correlation. b. Compute the Pearson correlation.
> a. A researcher computes the linear regression equation for a sample of n = 20 pairs of scores, X and Y values. If an analysis of regression is used to test the significance of the equation, what are the df values for the F-ratio? b. A researcher evaluat
> Does the regression equation from Problem 25 account for a significant portion of the variance in the Y scores? Use a = .05 to evaluate the F-ratio. Problem: 25
> a. One set of 10 pairs of scores, X and Y values, produces a correlation of r = 0.60. If SSY = 200, find the standard error of estimate for the regression line. b. A second set of 10 pairs of X and Y values produces a correlation of r = 0.40. If SSY = 20
> For the following set of scores, find the value of each expression:
> The regression equation is computed for a set of n = 18 pairs of X and Y values with a correlation of r = +0.50 and SSY = 48. a. Find the standard error of estimate for the regression equation. b. How big would the standard error be if the sample size we
> For the following scores: a. Find the regression equation for predicting Y from X. b. Calculate the predicted Y value for each X.
> For the following data: a. Find the regression equation for predicting Y from X. b. Calculate the Pearson correlation for these data. Use r2 and SSY to compute SSresidual and the standard error of estimate for the equation.
> For the following set of data, compute the Pearson correlation statistic and find the linear regression equation for predicting Y from X:
> In general, how is the magnitude of the standard error of estimate related to the value of the correlation?
> Briefly explain what is measured by the standard error of estimate.
> A set of n = 15 pairs of scores (X and Y values) produces a regression equation of Y⁄ = 3X + 8. Find the predicted Y value for each of the following X scores: 1, 2, 3, and 6.
> Calculate SP (the sum of products of deviations) for the following scores. Note: Both means are decimal values, so the computational formula works well.
> A set of n = 18 pairs of scores (X and Y values) has SSX = 16, SSY = 64, and SP = 20. If the mean for the X values is MX = 6 and the mean for the Y values is MY = 8: a. Calculate the Pearson correlation for the scores. b. Find the regression equation for
> Sketch a graph showing the line for the equation Y = 2X - 1. On the same graph, show the line for Y = -X + 8.
> For the following set of scores: a. Construct a stem and leaf plot. b. What is the shape of the distribution?
> Problem 13 in Chapter 10 presented data demonstrating that participants who binge-watched a television series enjoyed the show less than participants who watched the series in daily sessions. In the study, one group watched the complete television series
> In Problem 14, do the data suggest that increased learning ability caused starlings to have greater social status? Explain. Problem 14:
> It appears that there is a significant relationship between cognitive ability and social status, at least for birds. Boogert, Reader, and Laland (2006) measured social status and individual learning ability for a group of starlings. The following data re
> For a two-tailed test with a = .05, use Table B.6 to determine how large a Pearson correlation is necessary to be statistically significant for each of the following samples: a. A sample of n = 6 b. A sample of n = 12 c. A sample of n = 24
> In recent years, researchers have differentiated between two types of Internet harassment: cyberbullying and Internet trolling. In a recent study of cyber harassment, a large sample of online participants answered survey questions related to personality,
> Judge and Cable (2010) demonstrated a positive relationship between weight and income for a group of men. The following are data similar to those obtained in the study. To simplify the weight variable, the men are classified into five categories that mea
> For the following set of scores, a. Compute the Pearson correlation. b. Add 2 points to each X value and compute the correlation for the modified scores. How does adding a constant to every score affect the value of the correlation? c. Multiply each of t
> Calculate SP (the sum of products of deviations) for the following scores. Note: Both means are whole numbers, so the definitional formula works well.
> A researcher conducts an independent-measures, two-factor study with two levels of factor A and three levels of factor B, using a sample of n = 10 participants in each treatment condition. a. What are the df values for the F-ratio evaluating the main eff
> The following matrix presents the results of a two-factor study with n = 10 scores in each of the six treatment conditions. Note that one of the treatment means is missing. a. What value for the missing mean would result in no main effect for factor A? b
> Ford and Torok (2008) found that motivational signs were effective in increasing physical activity on a college campus. Signs such as “Step up to a healthier lifestyle” and “An average person burns 10 calories a minute walking up the stairs” were posted
> Suppose that a researcher was interested in the effect of caffeine on memory. She measured memory performance either immediately after studying (0-day delay) or after a 10-day delay. Half of the participants in each delay group received either a cup of d
> Eyewitnesses in jury trials are influenced by memory processes like forgetting. Jurors seem to also be influenced by instructions that encourage skepticism and the language used in eyewitness testimony. In a recent study of jury decision making (Kurinec
> The diathesis stress approach to mental illness proposes that neither environmental stress alone nor genetic factors alone are enough to produce mental illness. Instead, both environmental stress and genetic predisposition to mental illness are required
> The following table summarizes the results from a two-factor study with two levels of factor A and three levels of factor B using a separate sample of n = 8 participants in each treatment condition. Fill in the missing values. (Hint: Start with the df va
> The following table summarizes the results from a two-factor study with two levels of factor A and three levels of factor B using a separate sample of n = 5 participants in each treatment condition. Fill in the missing values. (Hint: Start with the df va
> The following results are from an independent-measures, two-factor study with n = 4 participants in each treatment condition. Use a two-factor ANOVA with a = .05 to evaluate the main effects and the interaction.
> A researcher reports an F-ratio with dfbetween = 3 and dfwithin = 40 for an independent-measures ANOVA. a. How many treatment conditions were compared in the experiment? b. How many subjects participated in the experiment? c. Use Appendix B to find the c
> A researcher uses an ANOVA to compare six treatment conditions with a sample of n = 12 in each treatment. For this analysis, find dftotal, dfbetween, and dfwithin.
> Calculate SStotal, SSbetween, and SSwithin for the following set of data:
> Calculate SStotal, SSbetween, and SSwithin for the following set of data:
> Your instructors, your parents, and your feelings of stress during finals week all tell you that cramming is a bad way to prepare for exams. Participants in Kornell’s (2009) research study received two sets of flash cards with vocabular
> Describe some of the reasons that group means might be different from each other in an analysis of variance. Describe some of the reasons that individual scores might be different from each other.
> An ANOVA produces an F-ratio with df = 1, 34. Could the data have been analyzed with a t test? What would be the degrees of freedom for the t statistic?
> What value is expected for the F-ratio, on average, if the null hypothesis is true in an ANOVA? Explain why.
> The following data were observed in an independent-measures study comparing three treatment conditions. a. Use an ANOVA with a = .05 to determine whether there are any significant differences among the three treatment means. Note: Because the samples are
> The following data were obtained from an independent-measures study comparing three treatment conditions. a. Calculate the sample variance for each of the three samples. b. Use an ANOVA with a = .05 to determine whether there are any significant differen
> A researcher used ANOVA and computed F = 4.25 for the following data. a. If the mean for Treatment III were changed to M = 25, what would happen to the size of the F-ratio (increase or decrease)? Explain your answer. b. If the SS for Treatment I were cha
> Several factors influence the size of the F-ratio. For each of the following, indicate whether it would influence the numerator or the denominator of the F-ratio, and indicate whether the size of the F-ratio would increase or decrease. a. Increase the di
> A research report from an independent-measures study states that there are significant differences between treatments, F(4, 40) = 3.45, p < .05. a. How many treatment conditions were compared in the study? b. What was the total number of participants in
> The following values are from an independent-measures study comparing three treatment conditions. a. Compute the variance for each sample. b. Compute MSwithin, which would be the denominator of the F-ratio for an ANOVA. Because the samples are all the sa
> A research study comparing three treatment conditions produces T = 28 with n = 7 for the first treatment, T = 32 with n = 8 for the second treatment, and T = 108 with n = 9 for the third treatment. Calculate SSbetween treatments for these data.
> Weinstein, McDermott, and Roediger (2010) published an experimental study examining different techniques that students use to prepare for a test. Students read a passage, knowing that they would have a quiz on the material. After reading the passage, stu

