Question: The table shows the numbers of cell
The table shows the numbers of cell phone subscribers (in millions) in the United States for selected years. (Source: CTIA-The Wireless Association)
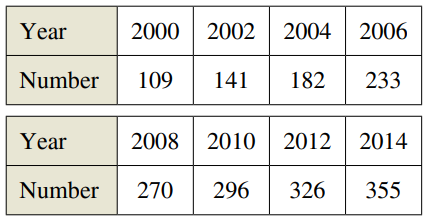
Use the regression capabilities of a graphing utility to find a mathematical model of the form y = at2 + bt + c for the data. In the model, y represents the number of subscribers (in millions) and t represents the year, with t = 0 corresponding to 2000.
Use a graphing utility to plot the data and graph the model. Compare the data with the model.
Use the model to predict the number of cell phone subscribers in the United States in the year 2024.
> Find an equation of the line that passes through the point and has the indicated slope. Then sketch the line. Point: (-8, 1) Slope: m is undefined
> Find an equation of the line that passes through the point and has the indicated slope. Then sketch the line. Point: (3, -5) Slope: m = 7/4
> Plot the pair of points and find the slope of the line passing through them. (-7, 8) , (-1, 8)
> Plot the pair of points and find the slope of the line passing through them. (3/2, 1) , (5, 5/2)
> Find any intercepts.
> Find the points of intersection of the graphs of the equations. x2 + y2 = 1 -x + y = 1
> Find the points of intersection of the graphs of the equations. x − y = −5 x2 – y = 1
> Find the points of intersection of the graphs of the equations. 2x + 4y = 9 6x – 4y = 7
> Find the points of intersection of the graphs of the equations. 5x + 3y = −1 x – y = -5
> Consider the circle x2 + y2 − 6x − 8y = 0 as shown in the figure. Find the center and radius of the circle. Find an equation of the tangent line to the circle at the point (0, 0). Find an equation of the tangent line t
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = │x − 4│ − 4
> Sketch a graph of the function and find its domain and range. Use a graphing utility to verify your graph. f(x) = √9 − x2
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 2 √4-x
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y2 = 9 – x
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 9x − x3
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = −x2 + 4
> Find any intercepts. y = (x − 1)√x2 + 1
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. The graph of a function of x cannot have symmetry with respect to the x-axis.
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = −1/2x + 3
> Test for symmetry with respect to each axis and to the origin. xy = −2
> The function y = 3 cos(x/3) has a period that is three times that of the function y = cos x.
> Test for symmetry with respect to each axis and to the origin. y2 = x2 – 5
> Test for symmetry with respect to each axis and to the origin. y = x4 − x2 + 3
> Test for symmetry with respect to each axis and to the origin. y = x2 + 4x
> Amplitude is always positive.
> Find any intercepts. y = (x-3) √x + 4
> Plot the pair of points and find the slope of the line passing through them. (4, 6), (4, 1)
> Plot the pair of points and find the slope of the line passing through them. (0, 0), (-2, 3)
> Plot the pair of points and find the slope of the line passing through them. (3, −4), (5, 2)
> Estimate the slope of the line from its graph.
> Estimate the slope of the line from its graph.
> Estimate the slope of the line from its graph.
> Estimate the slope of the line from its graph.
> Sketch a graph of the function and find its domain and range. Use a graphing utility to verify your graph. f(x) = 1/4 x3 + 3
> Is it possible for two lines with positive slopes to be perpendicular? Why or why not?
> In the form y = mx + b, what does m represent? What does b represent?
> Match the equation with its graph. [The graphs are labeled (a), (b), (c), and (d).] y = -(3/2) x + 3
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If b2 − 4ac = 0 and a ≠ 0, then the graph of y = ax2 + bx + c has only one x-intercept.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If b2 − 4ac > 0 and a ≠ 0, then the graph of y = ax2 + bx + c has two x-intercepts.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If (−4, −5) is a point on a graph that is symmetric with respect to the y-axis, then (4, −5) is also a point on the graph.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If (−4, −5) is a point on a graph that is symmetric with respect to the x-axis, then (4, −5) is also a point on the graph.
> Use the graphs of the two equations to answer the questions below. What are the intercepts for each equation? Determine the symmetry for each equation. Determine the point of intersection of the two equations.
> A graph is symmetric with respect to one axis and to the origin. Is the graph also symmetric with respect to the other axis? Explain
> A graph is symmetric with respect to the x-axis and to the y-axis. Is the graph also symmetric with respect to the origin? Explain.
> Find any intercepts. y = x-3 / x-4
> Write an equation whose graph has intercepts at x = −(3/2), x = 4, and x = 5 /2. (There is more than one correct answer.)
> For what values of k does the graph of y2 = 4kx pass through the point? a. (1, 1) b. (2, 4) c. (0, 0) d. (3, 3)
> How can you check that an ordered pair is a point of intersection of two graphs?
> Find the sales necessary to break even (R = C) when the cost C of producing x units is C = 2.04x + 5600 and the revenue R from selling x units is R = 3.29x.
> The table shows the Gross Domestic Product, or GDP (in trillions of dollars), for 2009 through 2014. (Source: U.S. Bureau of Economic Analysis) Use the regression capabilities of a graphing utility to find a mathematical model of the form y = at + b fo
> Use a graphing utility to find the points of intersection of the graphs of the equations. Check your results analytically. y = -│2x - 3│ + 6 y = 6 - x
> Use a graphing utility to find the points of intersection of the graphs of the equations. Check your results analytically. y = √x+6 y = √-x2 -4x
> Use a graphing utility to find the points of intersection of the graphs of the equations. Check your results analytically. y = x4 − 2x2 + 1 y = 1 − x2
> Find any intercepts. y = x2 − 8x + 12
> Use a graphing utility to find the points of intersection of the graphs of the equations. Check your results analytically. y = x3 − 2x2 + x – 1 y = −x2 + 3x – 1
> Find the points of intersection of the graphs of the equations. x2 + y2 = 16 x + 2y = 4
> Find the points of intersection of the graphs of the equations. x2 + y2 = 5 x – y = 1
> Describe how to find the x- and y-intercepts of the graph of an equation.
> Find the points of intersection of the graphs of the equations. x = 3 − y2 y = x – 1
> Find the points of intersection of the graphs of the equations. x2 + y = 15 −3x + y = 11
> Find the points of intersection of the graphs of the equations. 3x − 2y = −4 4x + 2y = −10
> Find the points of intersection of the graphs of the equations. x + y = 8 4x − y = 7
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. x2 + 4y2 = 4
> Find any intercepts. y = 5x – 8
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. 3y2 – x = 9
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = │6 − x│
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 6 − │x│
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 10 /(x2 + 1)
> find the domain and range of the function. g(x) = x2 − 5
> Let R be the region consisting of the points (x, y) of the Cartesian plane satisfying both ∣x∣ − ∣y∣ ≤ 1 and ∣y∣ ≤ 1. Sketch the region R and find its area.
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 8 / x
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. x = y4 - 16
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. x = y3
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = √25 – x2
> Find any intercepts. y = x√16 – x2
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = x √x + 5
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = x3 – 4x
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = x3 + 2
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 2x2 + x
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 9 - x2
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = (2/3)x + 1
> Find the domain and range of the function. f(x) = 4x2
> Find any intercepts and test for symmetry. Then sketch the graph of the equation. y = 2 − 3x
> Test for symmetry with respect to each axis and to the origin. │y│ - x = 3
> Let d1 and d2 be the distances from the point (x, y) to the points (−1, 0) and (1, 0), respectively, as shown in the figure. Show that the equation of the graph of all points (x, y) satisfying d1d2 = 1 is (x2 + y2)2 = 2(x2 âˆ
> The function y = ½ sin 2x has an amplitude that is twice that of the function y = sin x.
> Test for symmetry with respect to each axis and to the origin. y = │x3 + x│
> Test for symmetry with respect to each axis and to the origin. y = x5 / 4-x2
> Prove that the function is even. f(x) = a2nx2n + a2n-2x2n−2 + . . . + a2x2 + a0
> Prove that the function is odd f(x) = a2nx2n + a2nx2n-2 + . . . + a3x3 + a1x
> Use a graphing utility to graph the polynomial functions p1(x) = x3 − x + 1 and p2(x) = x3 − x. How many zeros does each function have? Is there a cubic polynomial that has no zeros? Explain
> The horsepower H required to overcome wind drag on a certain automobile is H(x) = 0.00004636x3 where x is the speed of the car in miles per hour. a. Use a graphing utility to graph H. b. Rewrite H so that x represents the speed in kilometers per hour. [
> Water runs into a vase of height 30 centimeters at a constant rate. The vase is full after 5 seconds. Use this information and the shape of the vase shown to answer the questions when d is the depth of the water in centimeters and t is the time in second
> An electronically controlled thermostat is programmed to lower the temperature during the night automatically (see figure). The temperature T in degrees Celsius is given in terms of t, the time in hours on a 24-hour clock. Approximate T(4) and T(15).
> Determine whether the function f(x) = 0 is even, odd, both, or neither. Explain.
> Does the degree of a polynomial function determine whether the function is even or odd? Explain.
> Suppose the speakers in Exercise 13 are 4 meters apart and the sound intensity of one speaker is k times that of the other, as shown in the figure. To print an enlarged copy of the graph, go to MathGraphs.com. a. Find the equation of all locations (x, y)
> Give an example of functions f and g such that f ∘ g = g ∘ f and f(x) ≠ g(x).
> Test for symmetry with respect to each axis and to the origin.
> Can the graph of a one-to-one function intersect a horizontal line more than once? Explain.

