Question: The three cases in the First Derivative
The three cases in the First Derivative Test cover the situations one commonly encounters but do not exhaust all possibilities. Consider the functions f, g, and h whose values at 0 are all 0 and, for x ≠0,
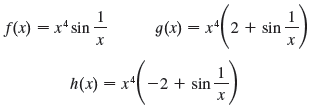
(a) Show that 0 is a critical number of all three functions but their derivatives change sign infinitely often on both sides of 0.
(b) Show that f has neither a local maximum nor a local minimum at 0, g has a local minimum, and h has a local maximum.
Transcribed Image Text:
f(x) = x*sin - g(x) = x 2 + sin - h(x) = x* -2 + sin
> A simply supported wood beam having a span length L = 12 ft is subjected to unsymmetrical point loads, as shown in the figure. Select a suitable size for the beam from the table in Appendix G. The allowable bending stress is 1800 psi and the wood weighs
> A thin strip of hard copper (E = 16,000 ksi) having length L = 90 in and thickness t = 3/32 in is bent into a circle and held with the ends just touching (see figure). (a) Calculate the maximum bending stress σmax in the strip. (b) By what per
> A cantilever beam is subjected to a concentrated moment at B. The length of the beam L = 3 m and the height h = 600 mm. The longitudinal strain at the top of the beam is 0.0005 and the distance from the neutral surface to the bottom surface of the beam i
> A simply supported beam with a length L = 10 ft and height 7 in. is bent by couples Mo into a circular arc with downward deflection d at the midpoint. If the curvature of the beam is 0.003 ft-1, calculate the deflection, d, at the mid-span of the beam an
> A bar of rectangular cross section is loaded and supported as shown in the figure. The distance between supports is L = 1.75 m, and the height of the bar is h = 140 mm. The deflection at the midpoint is measured as 2.5 mm. (a) What is the maximum normal
> A thin strip of steel with a length of L = 19 in and thickness of t = 0.275 in is bent by couples Mo (see figure). The deflection at the midpoint of the strip (measured from a line joining its end points) is found to be 0.30 in. (a) Determine the longitu
> A cantilever beam AB is loaded by a couple 0M at its free end (see figure). The length of the beam is L = 2.0 m, and the longitudinal normal strain at the top surface is ε = 0.0010. The distance from the top surface of the beam to the neutra
> A 4.75-in. outside diameter polyethylene pipe designed to carry chemical waste is placed in a trench and bent around a quarter-circular 908 bend (see figure). The bent section of the pipe is 52 ft long. (a) Determine the maximum compressive strain Î
> A copper wire having a diameter of d = 4mm is bent into a circle and held with the ends just touching (see figure). (a) If the maximum permissible strain in the copper is εmax = 0.0024, what is the shortest length L of wire that can be used?
> A palm tree weighing 1000 lb is inclined at an angle of 60° (see figure). The weight of the tree may be resolved into two resultant forces: a force P1 = 900 lb acting at a point 12 ft from the base and a force P2 = 100 lb acting at the top of
> A steel wire with a diameter of d = 1/16 in is bent around a cylindrical drum with a radius of R = 36 in (see figure). (a) Determine the maximum normal strain εmax. (b) What is the minimum acceptable radius of the drum if the maximum normal
> Beam ABCDE has a moment release just right of joint B and has concentrated moment loads at D and E. In addition, a cable with tension P is attached at F and runs over a pulley at C (Fig. a). The beam is constructed using two steel plates, which are welde
> A steel post (E = 3 0 × 106 psi) having thickness t = 1/8 in and height L = 72 in supports a stop sign (see figure), where s = 12.5 in. The height of the post L is measured from the base to the centroid of the sign. The stop sign is subjecte
> A foot bridge on a hiking trail is constructed using two timber logs each having a diameter d = 0.5 m (see figure a). The bridge is simply supported and has a length L = 4 m. The top of each log is trimmed to form the walking surface (see Fig. b). A simp
> A small dam of a height h = 6 ft is constructed of vertical wood beams AB, as shown in the figure. The wood beams, which have a thickness t = 2.5 in, are simply supported by horizontal steel beams at A and B. Construct a graph showing the maximum bending
> Consider the compound beam with segments AB and BCD joined by a pin connection (moment release) just right of B (see figure part a). The beam cross section is a double-T made up from three 50mm × 150 mm wood members (actual dimensions, see f
> A beam with a T-section is supported and loaded as shown in the figure. The cross section has width b = 21/2 in, height h = 3 in, and thickness t = 3/8 in. (a) Determine the maximum tensile and compressive stresses in the beam. (b) If the allowable stre
> A cantilever beam AB with a rectangular cross section has a longitudinal hole drilled throughout its length (see figure). The beam supports a load P = 600 N. The cross section is 25 mm wide and 50 mm high, and the hole has a diameter of 10 mm. Find the b
> A beam ABC with an overhang from B to C supports a uniform load of 200 lb/ft throughout its length (see figure). The beam is a channel section with dimensions as shown in the figure. The moment of inertia about the z axis (the neutral axis) equals 8.13 i
> A rigid frame ABC is formed by welding two steel pipes at B (see figure). Each pipe has cross- sectional area A = 11.31 × 103 mm2, moment of inertia I = 46.37 × 106 mm4, and outside diameter d = 200 mm Find the maximum tensile a
> A cantilever beam, a C12 × 30 section, is subjected to its own weight and a point load at B. Find the maximum permissible value of load P at B (kips) if the allowable stress in tension and compression is σa = 18 ksi. P q = 30
> A cantilever beam AB of an isosceles trapezoidal cross section has a length L = 0.8 m, dimensions b1 = 80 mm and b2 = 90 mm, and height h = 110 mm (see figure). The beam is made of brass weighing 85 kN/m3. (a) Determine the maximum tensile stress Ï&
> A cantilever beam AB, loaded by a uniform load and a concentrated load (see figure), is constructed of a channel section. (a) Find the maximum tensile stress σt and maximum compressive stress σc if the cross section has the dimensio
> Determine the maximum tensile stress σt and maximum compressive stress σc due to the load P acting on the simple beam AB (see figure). (a) Data are P = 6.2 kN, L = 3.2m, d = 1.25 m, b = 80 mm, t = 25 mm, h = 120 mm, and h1 = 90 mm.
> A simple beam AB of a span length L = 24 ft is subjected to two wheel loads acting at a distance d = 5 ft apart (see figure). Each wheel transmits a load P = 3.0 kips, and the carriage may occupy any position on the beam. (a) Determine the maximum bendin
> Determine the maximum bending stress σmax (due to pure bending by a moment M) for a beam having a cross section in the form of a circular core (see figure). The circle has diameter d and the angle β = 60°. -d-
> Determine the maximum tensile stress σt (due to pure bending about a horizontal axis through C by positive bending moments M) for beams having cross sections as follows (see figure). (a) A semicircle of diameter d. (b) An isosceles trapezoid w
> A small dam of height h = 2.0 m is constructed of vertical wood beams AB of thickness t = 120 mm, as shown in the figure. Consider the beams to be simply supported at the top and bottom. Determine the maximum bending stress σmax in the beams,
> A fiberglass pipe is lifted by a sling, as shown in the figure. The outer diameter of the pipe is 6.0 in., its thickness is 0.25 in, and its weight density is 0.053 lb/in3. The length of the pipe is L = 36 ft and the distance between lifting points is s
> A railroad tie (or sleeper) is subjected to two rail loads, each of magnitude P = 175 kN, acting as shown in the figure. The reaction q of the ballast is assumed to be uniformly distributed over the length of the tie, which has cross-sectional dimensions
> A curved bar ABC having a circular axis (radius r = 12 in.) is loaded by forces P = 400 lb (see figure). The cross section of the bar is rectangular with height h and thickness t. If the allowable tensile stress in the bar is 12,000 psi and the height h
> The horizontal beam ABC of an oil-well pump has the cross section shown in the figure. If the vertical pumping force acting at end C is 9 kips and if the distance from the line of action of that force to point B is 16 ft, what is the maximum bending stre
> During construction of a highway bridge, the main girders are cantilevered outward from one pier toward the next (see figure). Each girder has a cantilever length of 48 m and an I-shaped cross section with dimensions shown in the figure. The load on each
> A seesaw weighing 3 lb/ft of length is occupied by two children, each weighing 90 lb (see figure). The center of gravity of each child is 8 ft from the fulcrum. The board is 19 ft long, 8 in. wide, and 1.5 in. thick. What is the maximum bending stress in
> A freight-car axle AB is loaded approximately as shown in the figure, with the forces P representing the car loads (transmitted to the axle through the axle boxes) and the forces R representing the rail loads (transmitted to the axle through the wheels).
> Each girder of the lift bridge (see figure) is 180 ft long and simply supported at the ends. The design load for each girder is a uniform load of intensity 1.6 kips/ft. The girders are fabricated by welding three steel plates to form an I-shaped cross se
> Beam ABC has simple supports at A and B and an overhang from B to C. The beam is constructed from a steel W 16 × 31. The beam must carry its own weight in addition to uniform load q = 150 lb/ft. Determine the maximum tensile and compressive
> A simply supported wood beam AB with a span length L = 4 m carries a uniform load of intensity q = 5.8 kN/m (see figure). (a) Calculate the maximum bending stress σmax due to the load q if the beam has a rectangular cross section with width b
> A thin, high-strength steel rule (E = 30 × 106 psi) having a thickness t = 0.175 in and length L = 48 in is bent by couples Mo into a circular arc subtending a central angle α = 40° (see figure). (a) What is the maxi
> A steel wire (E = 200 GPa) of a diameter d = 1.25 mm is bent around a pulley of a radius Ro = 500 mm (see figure). (a) What is the maximum stress σmax in the wire? (b) By what percent does the stress increase or decrease if the radius of the p
> An aluminum pole for a street light weighs 4600Â N and supports an arm that weighs 660 N (see figure). The center of gravity of the arm is 1.2 m from the axis of the pole. A wind force of 300 N also acts in the (2y) direction at 9 m above the
> The graph of the derivative f 9 of a function f is shown. (a) On what intervals is f increasing or decreasing? (b) At what values of x does f have a local maximum or minimum? y y= f'(x) 2 4 6
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other; that is, every curve in one family is orthogonal to every curve in the oth
> The graph of the derivative f 9 of a function f is shown. (a) On what intervals is f increasing or decreasing? (b) At what values of x does f have a local maximum or minimum? y y = f'(x) + 2 4 6.
> Sketch the graph of a function that satisfies all of the given conditions. (a) f ‘(x) > 0 and f ‘‘(x) < 0 for all x (b) f ‘(x) < 0 and f ‘‘(x) > 0 for all x
> (a) State the First Derivative Test. (b) State the Second Derivative Test. Under what circumstances is it inconclusive? What do you do if it fails?
> Suppose you are given a formula for a function f. (a) How do you determine where f is increasing or decreasing? (b) How do you determine where the graph of f is concave upward or concave downward? (c) How do you locate inflection points?
> Use the given graph of f to find the following. (a) The open intervals on which f is increasing. (b) The open intervals on which f is decreasing. (c) The open intervals on which f is concave upward. (d) The open intervals on which f is concave downward.
> Use the given graph of f to find the following. (a) The open intervals on which f is increasing. (b) The open intervals on which f is decreasing. (c) The open intervals on which f is concave upward. (d) The open intervals on which f is concave downward.
> Suppose f is differentiable on an interval I and f ‘(x) > 0 for all numbers x in I except for a single number c. Prove that f is increasing on the entire interval I.
> Suppose that f ’’’ is continuous and f ‘(c) = f ’’(c) = 0, but f ’’’(c) > 0. Does f have a local maximum or minimum at c? Does f have a point of inflection at c?
> Show that the function g(x) = x |x | has an inflection point at (0, 0) but g ’’(0) does not exist.
> (a) Use the Product Rule twice to prove that if f , g, and h are differentiable, then s (fgh)’ = f’ gh +fg’ h + fgh’ . (b) Taking f = g = h in part (a), show that (c) Use part (b) to
> Sketch the graph of a function that satisfies all of the given conditions. (a) f ‘(x) < 0 and f ‘‘(x) < 0 for all x (b) f ‘(x) > 0 and f ‘‘(x) > 0 for all x
> Show that if f (x) = x4, then f ’’(0) = 0, but (0, 0) is not an inflection point of the graph of f .
> Prove that if (c, f (c)) is a point of inflection of the graph of f and f ’’ exists in an open interval that contains c, then f ’’(c) = 0.
> For what values of c does the polynomial P(x) = x4 + cx3 + x2 have two inflection points? One inflection point? None? Illustrate by graphing P for several values of c. How does the graph change as c decreases?
> Show that a cubic function (a third-degree polynomial) always has exactly one point of inflection. If its graph has three x-intercepts x1, x2, and x3, show that the x-coordinate of the inflection point is (x1 + x2 + x3)/3.
> Show that tan x > x for 0 < x < π/2.
> Suppose f and g are both concave upward on (-∞,∞). Under what condition on f will the composite function h(x) = f (g(x)) be concave upward?
> (a) If f and g are positive, increasing, concave upward functions on I, show that the product function fg is concave upward on I. (b) Show that part (a) remains true if f and g are both decreasing. (c) Suppose f is increasing and t is decreasing. Show, b
> Assume that all of the functions are twice differentiable and the second derivatives are never 0. (a) If f and g are concave upward on I, show that f + g is concave upward on I. (b) If f is positive and concave upward on I, show that the function g(x) =
> Show that the inflection points of the curve y = x sin x lie on the curve y2(x2 + 4) = 4x2.
> Suppose f ‘ is continuous on (-∞, ∞). (a) If f (2) = 0 and f ’’(2) = -5, what can you say about f ? (b) If f ‘(6) = 0 and f ’’(6) = 0, what can you say about f ?
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other; that is, every curve in one family is orthogonal to every curve in the oth
> Show that the curves y = e-x and y = -e-x touch the curve y = e-x sin x at its inflection points.
> Show that the curve y = (1 + x)/(1 + x2) has three points of inflection and they all lie on one straight line.
> For what values of a and b is (2, 2.5) an inflection point of the curve x2y + ax + by = 0? What additional inflection points does the curve have?
> (a) If the function f (x) = x3 + ax2 + bx has the local minimum value − 2 9 3 at x = 1/ 3 , what are the values of a and b? (b) Which of the tangent lines to the curve in part (a) has the smallest slope?
> Find a cubic function f (x) = ax3 + bx2 + cx + d that has a local maximum value of 3 at x = -2 and a local minimum value of 0 at x = 1.
> A drug response curve describes the level of medication in the bloodstream after a drug is administered. A surge function S(t) = Atpe-kt is often used to model the response curve, reflecting an initial surge in the drug level and then a more gradual decl
> (a) Find the critical numbers of f (x) = x4(x – 1)3. (b) What does the Second Derivative Test tell you about the behavior of f at these critical numbers? (c) What does the First Derivative Test tell you?
> Coffee is being poured into the mug shown in the figure at a constant rate (measured in volume per unit time). Sketch a rough graph of the depth of the coffee in the mug as a function of time. Account for the shape of the graph in terms of concavity. Wha
> Let K(t) be a measure of the knowledge you gain by studying for a test for t hours. Which do you think is larger, K(8) – K(7) or K(3) – K(2)? Is the graph of K concave upward or concave downward? Why?
> Two curves are orthogonal if their tangent lines are perpendicular at each point of intersection. Show that the given families of curves are orthogonal trajectories of each other; that is, every curve in one family is orthogonal to every curve in the oth
> Let f (t) be the temperature at time t where you live and suppose that at time t = 3 you feel uncomfortably hot. How do you feel about the given data in each case? (a) f ‘(3) = 2, f ‘(3) = 4 (b) f ‘(3) = 2, f ‘(3) = 24 (c) f ‘(3) = 22, f ‘(3) = 4 (d) f ‘
> The president announces that the national deficit is increasing, but at a decreasing rate. Interpret this statement in terms of a function and its first and second derivatives.
> In an episode of The Simpsons television show, Homer reads from a newspaper and announces “Here’s good news! According to this eye-catching article, SAT scores are declining at a slower rate.” Interpret Homer’s statement in terms of a function and its fi
> A graph of a population of yeast cells in a new laboratory culture as a function of time is shown. (a) Describe how the rate of population increase varies. (b) When is this rate highest? (c) On what intervals is the population function concave upward o
> Use the methods of this section to sketch the curve y = x3 - 3a2x + 2a3, where a is a positive constant. What do the members of this family of curves have in common? How do they differ from each other?
> Suppose the derivative of a function f is f (x) = (x + 1)2 (x – 3)5 (x – 6)4. On what interval is f increasing?
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = x2 - x - ln x
> Prove the formula for (d/dx)(cos-1x) by the same method as for (d/dx)(sin-1x).
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = x2 ln x
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = e2x + e-x
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) =cos2x - 2 sin x, 0 ≤ x ≤ 2π
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) =sin x + cos x, 0 ≤ x ≤ 2 π
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = x4 - 2x2 + 3
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = 2x3 - 9x2 + 12x - 3
> (a) Find the intervals on which f is increasing or decreasing. (b) Find the local maximum and minimum values of f. (c) Find the intervals of concavity and the inflection points. f(x) = x3 - 3x2 - 9x + 4
> The graph of the first derivative f ‘ of a function f is shown. (a) On what intervals is f increasing? Explain. (b) At what values of x does f have a local maximum or minimum? Explain. (c) On what intervals is f concave upward or concav
> In each part state the x-coordinates of the inflection points of f. Give reasons for your answers. (a) The curve is the graph of f. (b) The curve is the graph of f ‘. (c) The curve is the graph of f ’’
> Verify that the function satisfies the three hypotheses of Rolle’s Theorem on the given interval. Then find all numbers c that satisfy the conclusion of Rolle’s Theorem. f(x) = sin (x/2), [π/2, 3π/2]
> Draw the graph of a function that is continuous on [0, 8] where f (0) = 1 and f (8) = 4 and that does not satisfy the conclusion of the Mean Value Theorem on [0, 8].
> The graph of a function t is shown. (a) Verify that t satisfies the hypotheses of the Mean Value Theorem on the interval [0, 8]. (b) Estimate the value(s) of c that satisfy the conclusion of the Mean Value Theorem on the interval [0, 8]. (c) Estimate t
> Draw the graph of a function defined on [0, 8] such that f (0) = f (8) = 3 and the function does not satisfy the conclusion of Rolle’s Theorem on [0, 8].
> The graph of a function f is shown. Verify that f satisfies the hypotheses of Rolle’s Theorem on the interval [0, 8]. Then estimate the value(s) of c that satisfy the conclusion of Rolle’s Theorem on that interval.
> A number a is called a fixed point of a function f if f (a) = a. Prove that if f ‘(x) ≠ 1 for all real numbers x, then f has at most one fixed point.
> Find the derivative of the function. Simplify where possible. y = cos-1(sin-1 t)
> Two runners start a race at the same time and finish in a tie. Prove that at some time during the race they have the same speed.

