Question: The widths (in meters) of a kidney-
The widths (in meters) of a kidney-shaped swimming pool were measured at 2-meter intervals as indicated in the figure. Use the Midpoint Rule to estimate the area of the pool.
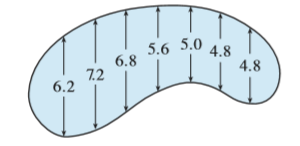
Transcribed Image Text:
5.6 5.0 6.8 7.2 4.8 4.8 6.2
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R2 about AB
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R2 about OC
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у 3 sin x, у—2х/п, х>0 y
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R2 about OA
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R1 about BC
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R, about AB
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) R1 about OC
> Refer to the figure and find the volume generated by rotating the given region about the specified line. C(0, 1)| R2 B(1, 1) y= Vx A(1, 0) Rj about OA
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — х, у — 0, х — 2, х — 4; about x
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. x = y', x = 1 – y²; about x = 3
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. ху— 1, у — 0, х — 1, х— 2;B about x -
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —х', у — 0, х — 1; about x
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = sin x, y = cos x, 0 < x </4; about y = -1
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у — 1/х, у — 1/х, х—2 y
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = 1 + sec x, y = 3; about y = 1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — х", у — 1, х — 2;B about y — -3 |3D
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —х, х — у?;B аbout y — 1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. х — 2 — у?, х —у%;B about the y-aхis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y² = x, x = 2y; about the y-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = 6 – x², y = 2; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = x', y = x, x> 0; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. 2х — у?, х — 0, у — 4;B about the y-ахis
> Suppose that a region / has area A and lies above the x-axis. When / is rotated about the x-axis, it sweeps out a solid with volume V1. When / is rotated about the line y = -k (where k is a positive number), it sweeps out a solid with volume V2. Express
> Some of the pioneers of calculus, such as Kepler and Newton, were inspired by the problem of finding the volumes of wine barrels. (In fact Kepler published a book Stereometria doliorum in 1615 devoted to methods for finding the volumes of barrels.) They
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у — х3 — 4х, у %3 2х y
> A hole of radius r is bored through the center of a sphere of radius R > r. Find the volume of the remaining portion of the sphere.
> A hole of radius r is bored through the middle of a cylinder of radius R < r at right angles to the axis of the cylinder. Set up, but do not evaluate, an integral for the volume cut out.
> A bowl is shaped like a hemisphere with diameter 30 cm. A heavy ball with diameter 10 cm is placed in the bowl and water is poured into the bowl to a depth of h centimeters. Find the volume of water in the bowl.
> Find the volume common to two spheres, each with radius r, if the center of each sphere lies on the surface of the other sphere.
> Find the volume common to two circular cylinders, each with radius r, if the axes of the cylinders intersect at right angles.
> (a) Cavalieri’s Principle states that if a family of parallel planes gives equal cross-sectional areas for two solidsS1 and S2, then the volumes of S1 and S2 are equal. Prove this principle. (b) Use Cavalieri’s Princip
> Solve Example 9 taking cross-sections to be parallel to the line of intersection of the two planes.
> (a) Set up an integral for the volume of a solid torus (the donut-shaped solid shown in the figure) with radii r and R. (b) By interpreting the integral as an area, find the volume of the torus. R-
> The base of S is a circular disk with radius r. Parallel cross sections perpendicular to the base are isosceles triangles with height h and unequal side in the base. (a) Set up an integral for the volume of S. (b) By interpreting the integral as an area,
> For what values of m do the line y = mx and the curve / enclose a region? Find the area of the region.
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у 3 (х — 2), у %3Dх 2)°, y = y =
> Suppose that /. For what value of c is the area of the region enclosed by the curves y = cos x, / equal to the area of the region enclosed by the curves /
> Find the values of c such that the area of the region bounded by the parabolas /
> (a) Find the number a such that the line x − a bisects the area under the curve / (b) Find the number b such that the line y = b bisects the area in part (a).
> Find the number b such that the line y = b divides the region bounded by the curves y = x2 and y = 4 into two regions with equal area.
> Find the area of the region bounded by the parabola y = x2, the tangent line to this parabola at (1, 1), and the x-axis.
> The curve with equation / is called Tschirnhausen’s cubic. If you graph this curve you will see that part of the curve forms a loop. Find the area enclosed by the loop.
> The figure shows graphs of the marginal revenue function R9 and the marginal cost function C9 for a manufacturer. [Recall from Section 4.7 that R(x) and C(x) represent the revenue and cost when x units are manufactured. Assume that R and C are measured i
> Two cars, A and B, start side by side and accelerate from rest. The figure shows the graphs of their velocity functions. (a) Which car is ahead after one minute? Explain. (b) What is the meaning of the area of the shaded region? (c) Which car is ahead af
> The rates at which rain fell, in inches per hour, in two different locations t hours after the start of a storm are given by / and / Compute the area between the graphs for / and interpret your result in this context.
> In Example 5, we modeled a measles pathogenesis curve by a function f. A patient infected with the measles virus who has some immunity to the virus has a pathogenesis curve that can be modeled by, for instance, / (a) If the same threshold concentration
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у 3 sin x, у — х, х— п/2, х— п
> If the birth rate of a population is / people per year and the death rate is / people per year, find the area between these curves for / What does this area represent?
> A cross-section of an airplane wing is shown. Measurements of the thickness of the wing, in centimeters, at 20-centimeter intervals are 5.8, 20.3, 26.7, 29.0, 27.6, 27.3, 23.8, 20.5, 15.1, 8.7, and 2.8. Use the Midpoint Rule to estimate the area of the w
> Racing cars driven by Chris and Kelly are side by side at the start of a race. The table shows the velocities of each car (in miles per hour) during the first ten seconds of the race. Use the Midpoint Rule to estimate how much farther Kelly travels than
> Sketch the region in the xy-plane defined by the inequalities / and find its area.
> Use a computer algebra system to find the exact area enclosed by the curves y = x5 - 6x3 + 4x and y = x.
> Graph the region between the curves and use your calculator to compute the area correct to five decimal places. у — cos x, у —х+2 sin'x y
> Graph the region between the curves and use your calculator to compute the area correct to five decimal places. y = у — tan?x, у — x
> Graph the region between the curves and use your calculator to compute the area correct to five decimal places. y = e' *, y=x*
> Graph the region between the curves and use your calculator to compute the area correct to five decimal places. 2 y = 1 + x* y = x?
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. y = e", y = x? – 1, x=-1, x= 1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. у — 1.3, у— 2
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. у — Зx? — 2х, у—х3 — Зх + 4
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = (x² + 1)²' y = x' – x, x>0
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. у —х sin(x"), у — х", x> 0 y y
> Evaluate the integral and interpret it as the area of a region. Sketch the region. L,13* – 2*| dx
> Evaluate the integral and interpret it as the area of a region. Sketch the region. 1/2 " | sin x – cos 2x| dx
> Use calculus to find the area of the triangle with the given vertices. (2, 0), (0,2), (-1, 1)
> Use calculus to find the area of the triangle with the given vertices. (0, 0), (3, 1), (1, 2)
> Sketch the region enclosed by the given curves and find its area. In x y = - (In x)² y =
> Sketch the region enclosed by the given curves and find its area. x² y 1+ x? y 1 + x³
> Find the area of the shaded region. 4. yA x= y? – 4y (-3, 3) x= 2y – y²
> Find the area of the shaded region. y AI y=r (1, 1) x= 8 y = 1/x
> Use the graph of
> Use your computer algebra system to differentiate
> Use a graph of
> Show that where And a² + b² – 625 0 = arccoS 2ab a? = (9 + x cos a)² + (31 – x sin a)? b? = (9 + x cos a)² + (x sin a – 6)²
> power model often provides a more accurate fit than a quadratic model for a Lorenz function. If you have a computer with Maple or Mathematica, fit a power function (y – axk) to the data in Problem 2 and use it to estimate the Gini index
> The following table gives values for the Lorenz function in the years 1970, 1980, 1990, and 2000. Use the method of Problem 2 to estimate the Gini index for the United States for those years and compare with your answer to Problem 2(c). Do you notice a t
> The following table (derived from data supplied by the US Census Bureau) shows values of the Lorenz function for income distribution in the United States for the year 2010. (a) What percentage of the total US income was received by the richest 20% of t
> (a) Show that the Gini index G is twice the area between the Lorenz curve and the line y = x, that is, (b) What is the value of G for a perfectly egalitarian society (everybody has the same income)? What is the value of G for a perfectly totalitarian soc
> Find the average value of the function on the given interval. f(t) = esin cos t, [0, 7/2]
> Sketch the region enclosed by the given curves and find its area. x> 0 y /1 + x y 9 - x
> Find the average value of the function on the given interval. g(t) [1, 3] /3 + t²
> A variable force of 5x22 pounds moves an object along a straight line when it is x feet from the origin. Calculate the work done in moving the object from x = 1 ft to x = 10 ft.
> How much work is done when a hoist lifts a 200-kg rock to a height of 3 m?
> A 360-lb gorilla climbs a tree to a height of 20 ft. Find the work done if the gorilla reaches that height in (a) 10 seconds (b) 5 seconds
> If f is a continuous function, what is the limit as h → 0 of the average value off on the interval [x, x + h]?
> Find the average value of the function f(t) − sec2t on the interval [0,
> A force of 30 N is required to maintain a spring stretched from its natural length of 12 cm to a length of 15 cm. How much work is done in stretching the spring from 12 cm to 20 cm?
> Each integral represents the volume of a solid. Describe the solid. 2пх сos x dx
> Each integral represents the volume of a solid. Describe the solid. 1/2 2T cos'x dx Jo
> The linear density in a rod 8 m long is / where x is measured in meters from one end of the rod. Find the average density of the rod.
> The graphs of two functions are shown with the areas of the regions between the curves indicated. (a) What is the total area between the curves for 0 < x< 5? (b) What is the value of f [f(x) – g(x)]dx? y 27 12 4 3. 2.
> Find the average value of the function on the given interval. S(к) — х?/(х3 + 3)?, [-1, 1]
> Find the average value of the function on the given interval. д(х) — 3 сos x, [-п/2, п/2]
> Find the average value of the function on the given interval. f(x) = /x, [0, 4]
> Find the average value of the function on the given interval. f(x) — Зх? + 8x, [-1,2] –1, 2]
> The table shows values of a force function f(x) where x is measured in meters and f(x) in newtons. Use the Midpoint Rule to estimate the work done by the force in moving an object from x = 4 to x = 20. 68 10 1 4 12| 14 16 18 f(x) 5.8 7.0 | 8.8 | 9.6
> The figure shows a horizontal line y = c intersecting the curve y = 8x - 27x3. Find the number c such that the areas of the shaded regions are equal.
> There is a line through the origin that divides the region bounded by the parabola y = x - x2 and the x-axis into two regions with equal area. What is the slope of that line?
> (a) Find a positive continuous function f such that the area under the graph off from 0 to t is A(t) = t3 for all t. 0. (b) A solid is generated by rotating about the x-axis the region under the curve y – f(x), where f is a positive function and x > 0.
> If the tangent at a point P on the curve y = x3 intersects the curve again at Q, let A be the area of the region bounded by the curve and the line segment PQ. Let B be the area of the region defined in the same way starting with Q instead of P. What is t
> Suppose we are planning to make a taco from a round tortilla with diameter 8 inches by bending the tortilla so that it is shaped as if it is partially wrapped around a circular cylinder. We will fill the tortilla to the edge (but no more) with meat, chee

