Question: To defrost ice accumulated on the outer
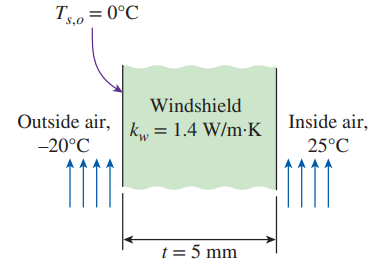
To defrost ice accumulated on the outer surface of an automobile windshield, warm air is blown over the inner surface of the windshield. Consider an automobile windshield (kw = 1.4 W/m⋅K) with an overall height of 0.5 m and thickness of 5 mm. The outside air (1 atm) ambient temperature is −20°C, and the average airflow velocity over the outer windshield surface is 80 km/h, while the ambient temperature inside the automobile is 25°C. Determine the value of the convection heat transfer coefficient for the warm air blowing over the inner surface of the windshield that is needed to cause the accumulated ice to begin melting. Assume the windshield surface can be treated as a flat plate surface.
> Hydrogen gas at 1 atm is flowing in parallel over the upper and lower surfaces of a 3-m-long flat plate at a velocity of 2.5 m/s. The gas temperature is 120°C, and the surface temperature of the plate is maintained at 30°C. Using appropriate software, in
> Parallel plates form a solar collector that covers a roof, as shown in the figure. The plates are maintained at 15°C, while ambient air at 10°C flows over the roof with V = 2 m/s. Determine the rate of convective heat loss from (a)
> Consider a TV set that consumes 120 W of electric power when it is on and is kept on for an average of 6 h per day. For a unit electricity cost of 12 cents per kWh, determine the cost of electricity this TV consumes per month (30 days).
> Hot engine oil at 150°C is flowing in parallel over a flat plate at a velocity of 2 m/s. Surface temperature of the 0.5-m-long flat plate is constant at 50°C. Determine (a) the local convection heat transfer coefficient at 0.2 m from the leading edge and
> Hot carbon dioxide exhaust gas at 1 atm is being cooled by flat plates. The gas at 220°C flows in parallel over the upper and lower surfaces of a 1.5-m-long flat plate at a velocity of 3 m/s. If the flat plate surface temperature is maintained at 80°C, d
> Water at 43.3°C flows over a large plate at a velocity of 30.0 cm/s. The plate is 1.0 m long (in the flow direction), and its surface is maintained at a uniform temperature of 10.0°C. Calculate the steady rate of heat transfer per unit width of the plate
> A desktop computer is to be cooled by a fan. The electronic components of the computer consume 80 W of power under full-load conditions. The computer is to operate in environments at temperatures up to 50°C and at elevations up to 3000 m where the atmosp
> In an experiment, the local heat transfer over a flat plate was correlated in the form of the local Nusselt number as expressed by the following correlation Nux = 0.035Rex0.8Pr1/3 Determine the ratio of the average convection heat transfer coefficient (h
> 100 kg/s of crude oil is heated from 20°C to 40°C through the tube side of a multitube heat exchanger. The crude oil flow is divided evenly among all 100 tubes in the tube bundle. The ID of each tube is 10 mm, and the inside tube-wall temperature is main
> Cold air at 5°C enters a 12-cm-diameter, 20-m-long isothermal pipe at a velocity of 2.5 m/s and leaves at 19°C. Estimate the surface temperature of the pipe.
> Geothermal steam at 165°C condenses in the shell side of a heat exchanger over the tubes through which water flows. Water enters the 4-cm-diameter, 14-m-long tubes at 20°C at a rate of 0.8 kg/s. Determine the exit temperature of water and the rate of con
> Hot exhaust gases leaving a stationary diesel engine at 450°C enter a 15-cm-diameter pipe at an average velocity of 7.2 m/s. The surface temperature of the pipe is 180°C. Determine the pipe length if the exhaust gases are to leave the pipe at 250°C after
> Repeat Prob. 19–121 for a pipe made of copper (k = 386 W/m⋅K) instead of cast iron. Data from Prob. 19-121: Hot water at 90°C enters a 15-m section of a cast iron pipe (k = 52 W/m⋅K) whos
> The force required to expand the gas in a gas spring a distance x is given by F = Constant / xk where the constant is determined by the geometry of this device and k is determined by the gas used in the device. Such a gas spring is arranged to have a con
> Hot water at 90°C enters a 15-m section of a cast iron pipe (k = 52 W/m⋅K) whose inner and outer diameters are 4 and 4.6 cm, respectively, at an average velocity of 1.2 m/s. The outer surface of the pipe, whose emissivity is
> Air is flowing through a smooth, thin-walled, 4-in-diameter copper tube that is submerged in water. The water maintains a constant temperature of 60°F and a convection heat transfer coefficient of 176 Btu/hâ‹…ft2â‹&#
> During air cooling of oranges, grapefruit, and tangelos, the heat transfer coefficient for combined convection, radiation, and evaporation for air velocities of 0.11
> The exhaust gases of an automotive engine leave the combustion chamber and enter an 8-ft-long and 3.5-in-diameter thin-walled steel exhaust pipe at 800°F and 15.5 psia at a rate of 0.05 lbm/s. The surrounding ambient air is at a temperature of 80°F, and
> Water at 1500 kg/h and 10°C enters a 10-mm-diameter smooth tube whose wall temperature is maintained at 49°C. Calculate (a) the tube length necessary to heat the water to 40°C, and (b) the water outlet temperature if the tube length is doubled. Assume av
> Repeat Prob. 19–116 for a flow rate of 20 kg/s. Data from Prob. 19-116: Water is heated at a rate of 10 kg/s from a temperature of 15°C to 35°C by passing it through five identical tubes, each 5.0 cm in diameter, whose surface temperature is 60.0°C. Est
> Water is heated at a rate of 10 kg/s from a temperature of 15°C to 35°C by passing it through five identical tubes, each 5.0 cm in diameter, whose surface temperature is 60.0°C. Estimate (a) the steady rate of heat transfer and (b) the length of tubes ne
> In the effort to find the best way to cool a smooth, thin-walled copper tube, an engineer decided to flow air either through the tube or across the outer tube surface. The tube has a diameter of 5 cm, and the surface temperature is held constant. Determi
> Liquid mercury is flowing at 0.6 kg/s through a 5-cm-diameter tube with inlet and outlet mean temperatures of 100°C and 200°C, respectively. The tube surface temperature is kept constant at 250°C. Determine the tube length using (a) the appropriate Nusse
> To cool a storehouse in the summer without using a conventional air-conditioning system, the owner decided to hire an engineer to design an alternative system that would make use of the water in the nearby lake. The engineer decided to flow air through a
> The force F required to compress a spring a distance x is given by F – F0 = kx where k is the spring constant and F0 is the preload. Determine the work, in kJ, required to compress a spring a distance of 1 cm when its spring constant is 300 N/cm and the
> Air (1 atm) enters a 5-mm-diameter circular tube at an average velocity of 5 m/s. The tube wall is maintained at a constant surface temperature. Determine the convection heat transfer coefficient for (a) a 10-cm-long tube and (b) a 50-cm-long tube. Evalu
> Crude oil at 22°C enters a 20-cm-diameter pipe with an average velocity of 32 cm/s. The average pipe wall temperature is 2°C. Crude oil properties are as given below. Calculate the rate of heat transfer and the pipe length if the cr
> A fluid (ρ = 1000 kg/m3, μ = 1.4 × 10−3 kg/m⋅s, cp = 4.2 kJ/kg⋅K, and k = 0.58 W/m⋅K) flows with an average velocity of 0.3 m/s through a 14-m-long tube with inside diameter of 0.01 m. Heat is uniformly added to the entire tube at the rate of 1500 W/m2.
> Consider airflow over a plate surface maintained at a temperature of 220°C. The temperature profile of the airflow is given as The airflow at 1 atm has a free stream velocity and temperature of 0.08 m/s and 20°C, respectively. Deter
> Repeat Prob. 19–108, assuming the inner surface of the tank to be at 0°C but by taking the thermal resistance of the tank and heat transfer by radiation into consideration. Assume the average surrounding surface temperature f
> During a fire, the trunks of some dry oak trees (k = 0.17 W/mâ‹…K and α = 1.28 × 10−7 m2/s) that are initially at a uniform temperature of 30°C are exposed to hot gases at 600Â
> A 0.55-m-internal-diameter spherical tank made of 1-cm-thick stainless steel (k = 15 W/m⋅K) is used to store iced water at 0°C. The tank is located outdoors at 30°C and is subjected to winds at 8 km/h. Assuming the
> In an annealing process, a 50-mm-thick stainless steel plate (ρ = 8238 kg/m3, cp = 468 J/kg⋅K, k = 13.4 W/m⋅K, and α = 3.48 × 10−6 m2/s ) was reheated in a furnace from an initial uniform temperature of 230°C. The ambient temperature inside the furnace
> Steam at 250°C flows in a stainless steel pipe (k = 15 W/m⋅K) whose inner and outer diameters are 4 cm and 4.6 cm, respectively. The pipe is covered with 3.5-cm-thick glass wool insulation (k = 0.038 W/m⋅K) whose outer surface has an emissivity of 0.3. H
> A transistor with a height of 0.32 in and a diameter of 0.22 in is mounted on a circuit board. The transistor is cooled by air flowing over it at a velocity of 600 ft/min. If the air temperature is 120°F and the transistor case temperature is
> A typical household pays about $1200 a year on energy bills, and the U.S. Department of Energy estimates that 46 percent of this energy is used for heating and cooling, 15 percent for heating water, 15 percent for refrigerating and freezing, and the rema
> A 4-kW resistance heater in a water heater runs for 3 hours to raise the water temperature to the desired level. Determine the amount of electric energy used in both kWh and kJ.
> During a picnic on a hot summer day, the only available drinks were those at the ambient temperature of 90°F. In an effort to cool a 12-fluid-oz drink in a can, which is 5 in high and has a diameter of 2.5 in, a person grabs the can and starts shaking it
> Consider a person who is trying to keep cool on a hot summer day by turning a fan on and exposing his body to airflow. The air temperature is 32°C, and the fan is blowing air at a velocity of 5 m/s. The surrounding surfaces are at 40°C, and the emissivit
> Aluminum wires 4 mm in diameter are produced by extrusion. The wires leave the extruder at an average temperature of 350°C and at a linear rate of 10 m/min. Before leaving the extrusion room, the wires are cooled to an average temperature of 50°C by tran
> In the effort to increase the removal of heat from a hot surface at 120°C, a cylindrical pin fin (kf = 237 W/m⋅K) with a diameter of 5 mm is attached to the hot surface. Air at 20°C (1 atm) is flowing across the pi
> A long roll of 2-m-wide and 0.5-cm-thick 1-Mn manganese steel plate coming off a furnace at 820°C is to be quenched in an oil bath (cp = 2.0kJ/kg⋅K) at 45°C. The metal sheet is moving at a steady velocity of 20 m/m
> An airstream at 1 atm flows, with a velocity of 15 m/s, in parallel over a 3-m-long flat plate where there is an unheated starting length of 1 m. The airstream has a temperature of 20°C, and the heated section of the flat plate is maintained at a constan
> Large steel plates 1.0 cm in thickness are quenched from 600°C to 100°C by submerging them in an oil reservoir held at 30°C. The average heat transfer coefficient for both faces of steel plates is 400 W/m2⋅K. Average steel properties are k = 45 W/m⋅K, ρ
> A 20-mm × 20-mm silicon chip is mounted such that the edges are flush in a substrate. The substrate provides an unheated starting length of 20 mm that acts as a turbulator. A turbulator is a device that trips the velocity boundary layer to turbulence. He
> A semi-infinite aluminum cylinder (k = 237 W/m⋅K, α = 9.71 × 10−5 m2/s) of diameter D = 15 cm is initially at a uniform temperature of Ti = 115°C. The cylinder is now placed in water at 10°C, where heat transfer takes place by convection with a heat tra
> The local atmospheric pressure in Denver, Colorado (elevation 1610 m), is 83.4 kPa. Air at this pressure and 20°C flows with a velocity of 8 m/s over a 1.5-m × 6-m flat plate whose temperature is 140°C. Determine the ra
> The U.S. Department of Energy estimates that 570,000 barrels of oil would be saved per day if every household in the United States lowered the thermostat setting in winter by 6°F (3.3°C). Assuming the average heating season to be 180 days and the cost of
> Reconsider Prob. 18–91. Using appropriate software, investigate the effect of the cooling time on the center temperature of the cylinder, the center temperature of the top surface of the cylinder, and the total heat transfer. Let the ti
> A short brass cylinder (ρ = 8530 kg/m3, cp = 0.389 kJ/kg⋅K, k = 110 W/m⋅K, and α = 3.39 × 10−5 m2/s) of diameter 4 cm and height 20 cm is initially at a uniform t
> A 2-cm-high cylindrical ice block (k = 2.22 W/m⋅K and α = 0.124 × 10−7 m2/s) is placed on a table on its base of diameter 2 cm in a room at 24°C. The heat transfer coefficient on the exposed surfaces of the ice block is 13 W/m2⋅K, and heat transfer from
> The upper surface of a 50-cm-thick solid plate (k = 237 W/m⋅K) is being cooled by water with temperature of 20°C. The upper and lower surfaces of the solid plate are maintained at constant temperatures of 60°C and
> Consider two identical 4-kg pieces of roast beef. The first piece is baked as a whole, while the second is baked after being cut into two equal pieces in the same oven. Will there be any difference between the cooking times of the whole and cut roasts? W
> What is forced convection? How does it differ from natural convection? Is convection that is caused by winds forced or natural convection?
> A hot dog can be considered to be a cylinder 5 in long and 0.8 in in diameter whose properties are ρ = 61.2 lbm/ft3, cp = 0.93 Btu/lbm⋅°F, k = 0.44 Btu/h⋅ft⋅°F, and α = 0.0077 ft2/h. A hot dog initially at 40°F is dropped into boiling water at 212°F. If
> Repeat Prob. 18–87 with the heat transfer coefficient at the top and the bottom surfaces of each block being doubled to 80 W/m2⋅K. Data from Prob. 18-87: Consider a cubic block whose sides are 5 cm long and a cylindri
> Consider a cubic block whose sides are 5 cm long and a cylindrical block whose height and diameter are also 5 cm. Both blocks are initially at 20°C and are made of granite (k = 2.5 W/mâ‹…K and α = 1.15 Ã
> A homeowner is considering these heating systems for heating his house: Electric resistance heating with $0.12/kWh and 1 kWh = 3600 kJ, gas heating with $1.24/therm and 1 therm = 105,500 kJ, and oil heating with $2.3/gal and 1 gal of oil = 138,500 kJ. As
> Consider a short cylinder whose top and bottom surfaces are insulated. The cylinder is initially at a uniform temperature Ti and is subjected to convection from its side surface to a medium at temperature T∞ with a heat transfer coefficient of h. Is the
> A short cylinder initially at a uniform temperature Ti is subjected to convection from all of its surfaces to a medium at temperature T∞. Explain how you can determine the temperature of the midpoint of the cylinder at a specified time t.
> How is the product solution used to determine the variation of temperature with time and position in three-dimensional systems?
> What is the product solution method? How is it used to determine the transient temperature distribution in a two dimensional system?
> A barefooted person whose feet are at 32°C steps on a large aluminum block at 20°C. Treating both the feet and the aluminum block as semi-infinite solids, determine the contact surface temperature. What would your answer be if the person stepped on a woo
> Thick slabs of stainless steel (k = 14.9 W/m⋅K and α = 3.95 × 10−6 m2/s) and copper (k = 401 W/m⋅K and α = 117 ×10−6 m2/s) are p
> We often cut a watermelon in half and put it into the freezer to cool it quickly. But usually we forget to check on it and end up having a watermelon with a frozen layer on top. To avoid this potential problem, a person wants to set a timer so that it wi
> Consider a potato being baked in an oven that is maintained at a constant temperature. The temperature of the potato is observed to rise by 5°C during the first minute. Will the temperature rise during the second minute be less than, equal to, or more th
> Reconsider Prob. 18–78. Using appropriate software, plot the soil temperature as a function of the distance from the earth’s surface as the distance varies from 0 m to 1 m, and discuss the results. Data from Prob. 18-
> The soil temperature in the upper layers of the earth varies with variations in the atmospheric conditions. Before a cold front moves in, the earth at a location is initially at a uniform temperature of 15°C. Then the area is subjected to a te
> Consider a homeowner who is replacing his 25-year-old natural gas furnace that has an efficiency of 55 percent. The home owner is considering a conventional furnace that has an efficiency of 82 percent and costs $1600 and a high-efficiency furnace that h
> A thick wood slab (k = 0.17 W/m⋅K and α = 1.28 ×10−7 m2/s) that is initially at a uniform temperature of 25°C is exposed to hot gases at 550°C for 5 min. The heat transfer coefficient between the gases and the wood slab is 35 W/m2⋅K. If the ignition temp
> Thick slabs of stainless steel (k = 14.9 W/m⋅K and α=3.95 × 10−6 m2/s) and copper (k=401 W/m⋅K and α=117 ×10−6 m2/s) are subject
> Refractory bricks are used as linings for furnaces, and they generally have low thermal conductivity to minimize heat loss through the furnace walls. Consider a thick furnace wall lined with refractory bricks (k = 1.0 W/mâ‹…K and Î&
> A thick aluminum block initially at 20°C is subjected to constant heat flux of 4000 W/m2 by an electric resistance heater whose top surface is insulated. Determine how much the surface temperature of the block will rise after 30 min.
> A highway made of asphalt is initially at a uniform temperature of 55°C. Suddenly the highway surface temperature is reduced to 25°C by rain. Determine the temperature at the depth of 3 cm from the highway surface and the heat flux transferred from the h
> A large cast iron container (k = 52 W/m⋅K and α = 1.70 × 10−5 m2/s) with 4-cm-thick walls is initially at a uniform temperature of 0°C and is filled with ice at 0°C. Now
> In areas where the air temperature remains below 0°C for prolonged periods of time, the freezing of water in underground pipes is a major concern. Fortunately, the soil remains relatively warm during those periods, and it takes weeks for the subfreezing
> Consider a curing kiln whose walls are made of 30-cm thick concrete with a thermal diffusivity of α=0.23 × 10−5 m2/s. Initially, the kiln and its walls are in equilibrium with the surroundings at 6°
> Consider heat transfer between two identical hot solid bodies and their environments. The first solid is dropped in a large container filled with water, while the second one is allowed to cool naturally in the air. For which solid is the lumped system an
> The walls of a furnace are made of 1.5-ft-thick concrete (k = 0.64 Btu/h⋅ft⋅°F and α = 0.023 ft2/h). Initially, the furnace and the surrounding air are in thermal equilibrium at 70°F. The furnace is then fired, and the inner surfaces of the furnace are s
> Consider a classroom for 55 students and one instructor, each generating heat at a rate of 100 W. Lighting is provided by 18 fluorescent lightbulbs, 40 W each, and the ballasts consume an additional 10 percent. Determine the rate of internal heat generat
> Consider a hot semi-infinite solid at an initial temperature of Ti that is exposed to convection to a cooler medium at a constant temperature of T∞, with a heat transfer coefficient of h. Explain how you can determine the total amount of heat transfer fr
> What is a semi-infinite medium? Give examples of solid bodies that can be treated as semi-infinite media for heat transfer purposes.
> Under what conditions can a plane wall be treated as a semi-infinite medium?
> Repeat Prob. 18–64 for a roast rib that is to be “welldone” instead of “rare.” A rib is considered to be well-done when its center temperature reaches 77°C, and the roasting in this case takes about 4 h 15 min. Data from Prob. 18-64: In Betty Crocker’s
> In Betty Crocker’s Cookbook, it is stated that it takes 2 h 45 min to roast a 3.2-kg rib initially at 4.5°C to “rare” in an oven maintained at 163°C. It is recommended that a meat thermometer be used to monitor the cooking, and the rib is considered rare
> A 9-cm-diameter potato (ρ=1100 kg/m3, cp =3900 J/kg⋅K, k = 0.6 W/m⋅K, and α = 1.4 × 10−7 m2/s) that is initially at a uniform temperature of 25°C is baked in an oven at 170°C until a temperature sensor inserted into the center of the potato indicates a r
> Explain how the fins enhance heat transfer from a surface. Also, explain how the addition of fins may actually decrease heat transfer from a surface.
> An experiment is to be conducted to determine the heat transfer coefficient on the surfaces of tomatoes that are placed in cold water at 7°C. The tomatoes (k = 0.59 W/m⋅K, α = 0.141 ×10−6 m2/s, ρ = 999 kg/m3, cp = 3.99 kJ/kg⋅K) with an initial uniform te
> White potatoes (k=0.50 W/m⋅K and α=0.13 × 10−6 m2/s) that are initially at a uniform temperature of 20°C and have an average diameter of 6 cm are to be cooled by refrigerated air a
> The fins attached to a surface are determined to have an effectiveness of 0.9. Do you think the rate of heat transfer from the surface has increased or decreased as a result of the addition of these fins?
> Some engineers have developed a device that provides lighting to rural areas with no access to grid electricity. The device is intended for indoor use. It is driven by gravity, and it works as follows: A bag of rock or sand is raised by human power to a
> Oranges of 2.5-in diameter (k = 0.26 Btu/h⋅ft⋅°F and α = 1.4 × 10−6 ft2/s) initially at a uniform temperature of 78°F are to be cooled by refrigerated air at 25°F flowing at a velocity of 1 ft/s. The average heat transfer coefficient between the oranges
> What is the difference between the fin effectiveness and the fin efficiency?
> Consider heat transfer between two identical hot solid bodies and the air surrounding them. The first solid is being cooled by a fan while the second one is allowed to cool naturally. For which solid is the lumped system analysis more likely to be applic
> What is the reason for the widespread use of fins on surfaces?
> Hot air is to be cooled as it is forced to flow through the tubes exposed to atmospheric air. Fins are to be added in order to enhance heat transfer. Would you recommend attaching the fins inside or outside the tubes? Why? When would you recommend attach
> Reconsider Prob. 18–58. Using appropriate software, investigate the effect of the final center temperature of the egg on the time it will take for the center to reach this temperature. Let the temperature vary from 50°C to 95
> Reconsider Prob. 17–93. Using appropriate software, plot the rate of heat transfer from the ball as a function of the plastic insulation thickness in the range of 0.5 mm to 20 mm. Discuss the results. Data from Prob. 17-93: A 4-mm-diam
> An ordinary egg can be approximated as a 5.5-cm diameter sphere whose properties are roughly k = 0.6 W/mâ‹…K and α = 0.14 × 10−6 m2/s. The egg is initially at a uniform temperature of 4Â&
> A 4-mm-diameter spherical ball at 50°C is covered by 1-mm-thick plastic insulation (k = 0.13 W/m⋅K). The ball is exposed to a medium at 15°C, with a combined convection and radiation heat transfer coefficient of 20

