Question: Two light sources of identical strength are
Two light sources of identical strength are placed 10 m apart.
An object is to be placed at a point P on a line l parallel to the line joining the light sources and at a distance meter from it (see the figure). We want to locate P on l so that the intensity of illumination is minimized. We need to use the fact that the intensity of illumination for a single source is directly proportional to the strength of the source and inversely proportional to the square of the distance from the source.
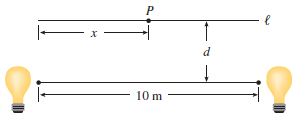
(a). Find an expression for the intensity I (x) at the point P.
(b). If d = 5m, use graphs of I (x) and I'(x) to show that the intensity is minimized when x = 5m, that is, when P is at the midpoint of l.
(c). If d = 10m, show that the intensity (perhaps surprisingly) is not minimized at the midpoint.
(d). Somewhere between d = 5m and d = 10m there is a transitional value of at which the point of minimal illumination abruptly changes. Estimate this value of d by graphical methods. Then find the exact value of d.
Transcribed Image Text:
P d 10 m
> The MSCI 2016 Survey of Women on Boards Survey showed that there continues to be a slow increase in the overall percentage of women on boards globally. The study reported that 69 of 70 (99%) French companies sampled, 39 of 53 (74%) German companies sampl
> What kinds of activities do you engage in when using a device while viewing video content on a TV screen? An IAB and MARU Matchbox study captured multitasking activities of adults who use different devices while watching TV. The study reported that 320 o
> Repeat (a) and (b) of Problem 12.16, assuming that only 100 individuals from each business group were surveyed. Discuss the implications of sample size on the χ2 test for differences among more than two populations. Problem 12.16: An Employee Value Prop
> An Employee Value Proposition (EVP) is about defining the essence of a company. The EVP is the value an employee receives from the employer; it defines the commitment the company will make to develop the employee in exchange for the effort the employee p
> Business sensor technology provides a way for companies to learn about their customers, employees, and operations; data captured from sensors can be used to improve engagement, sales, productivity, safety, and much more. A PwC survey of global business a
> How common are financial cost or contractual constraints associated with smartphone ownership? A survey of smartphone owners found that 48% of the 18- to 29-year-olds, 38% of the 30- to 49-year-olds, 25% of the 50- to 64-year-olds, and 19% of those age 6
> Use the following contingency table: a. Compute the expected frequency for each cell. b. Compute x2STAT. Is it significant at α = 0.05?
> The following ANOVA summary table is for a multiple regression model with two independent variables: a. Determine the regression mean square (MSR) and the mean square error (MSE). b. Compute the overall FSTAT test statistic. c. Determine whether the
> For this problem, use the following multiple regression equation: a. Interpret the meaning of the slopes. b. Interpret the meaning of the Y intercept.
> Use l’Hospital’s Rule to help find the asymptotes of f. Then use them, together with information from f' and f", to sketch the graph of f. Check your work with a graphing device. f(x) = (In x)/x
> Use l’Hospital’s Rule to help find the asymptotes of f. Then use them, together with information from f' and f", to sketch the graph of f. Check your work with a graphing device. f) — хе*
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Given that which of the following limits are indeterminate forms? For those that are not an indeterminate form, evaluate the limit where possible. lim f(x) = 0 lim g(x) = 0 lim h(x) = 1 %3D エ→ エ→ロ lim p(x) = 0 lim q(x) = 0 %3D (a) lim [f(x) – p(x)]
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Consider the following problem: A farmer with 750 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens? (a). Draw
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Given that which of the following limits are indeterminate forms? For those that are not an indeterminate form, evaluate the limit where possible. lim f(x) = 0 lim g(x) = 0 lim h(x) = 1 %3D エ→ エ→ロ lim p(x) = 0 lim q(x) = 0 %3D (b) lim [h(x)p(x)] (a
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. e f(x) = x2
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.
> Let (a). Show that f is continuous at 0. (b). Investigate graphically whether f is differentiable at by zooming in several times toward the point (0, 1) on the graph of f. (c). Show that f is not differentiable at 0. How can you reconcile this fact wi
> If f' is continuous, use l’Hospital’s Rule to show that Explain the meaning of this equation with the aid of a diagram. f(x + h) – f(x – h) lim = f'(x) 2h
> For what values of and is the following equation true? lim x→0 (sin 2x/x3 + a + b/x2)
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = 4x 32
> Investigate the family of curves given by f (x) = xe-cx, where c is a real number. Start by computing the limits as x→±∞. Identify any transitional values of where the basic shape changes. What happens to the maximum or minimum points and inflection poin
> (a). Graph the function. (b). Use l’Hospital’s Rule to explain the behavior as x→0. (c). Estimate the minimum value and intervals of concavity. Then use calculus to find the exact values. f(x) —
> The figure shows a sector of a circle with central angle θ. Let A (θ)be the area of the segment between the chord PR and the arc PR. Let B(θ) be the area of the triangle PQR. Find lim θâ†
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = x² –
> (a). Investigate the family of polynomials given by the equation f (x) = 2x3 + cx2 + 2x. For what values of does the curve have maximum and minimum points? (b). Show that the minimum and maximum points of every curve in the family lie on the curve y = x
> (a). Investigate the family of polynomials given by the equation f (x) = cx4 – 2x2 + 1. For what values of does the curve have minimum points? (b). Show that the minimum and maximum points of every curve in the family lie on the parabola y = 1 – x2. Illu
> Investigate the family of curves given by the equation f (x) = x4 + cx2 + x. Start by determining the transitional value of at which the number of inflection points changes. Then graph several members of the family to see what shapes are possible. There
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> If f' is the function considered in Example 3, use a computer algebra system to calculate f' and then graph it to confirm that all the maximum and minimum values are as given in the example. Calculate f" and use it to estimate the intervals of concavity
> Sketch the graph by hand using asymptotes and intercepts, but not derivatives. Then use your sketch as a guide to producing graphs (with a graphing device) that display the major features of the curve. Use these graphs to estimate the maximum and minimum
> Produce graphs of f that reveal all the important aspects of the curve. Estimate the intervals of increase and decrease and intervals of concavity, and use calculus to find these intervals exactly. 2 x 10 f(x - x*
> The speeds of sound c1 in an upper layer and c2 in a lower layer of rock and the thickness h of the upper layer can be determined by seismic exploration if the speed of sound in the lower layer is greater than the speed in the upper layer. A dynamite cha
> Investigate the family of curves given by f (x) = xne-x, where n is a positive integer. What features do these curves have in common? How do they differ from one another? In particular, what happens to the maximum and minimum points and inflection points
> Find the dimensions of a rectangle with area whose perimeter is as small as possible.
> Ornithologists have determined that some species of birds tend to avoid flights over large bodies of water during daylight hours. It is believed that more energy is required to fly over water than over land because air generally rises over land and falls
> (a). Graph the function. (b). Explain the shape of the graph by computing the limit as x→0 or as x→∞. (c). Estimate the maximum and minimum values and then use calculus to find the exact values. (d). Use a graph of f" to estimate the x-coordinates of the
> (a). Graph the function. (b). Explain the shape of the graph by computing the limit as x→0 or as x→∞. (c). Estimate the maximum and minimum values and then use calculus to find the exact values. (d). Use a graph of f" to estimate the x-coordinates of the
> (a). Graph the function. (b). Use l’Hospital’s Rule to explain the behavior as x→0. (c). Estimate the minimum value and intervals of concavity. Then use calculus to find the exact values. 1/1 f(x
> Find the maximum area of a rectangle that can be circumscribed about a given rectangle with length L and width W. [Hint: Express the area as a function of an angle θ.]
> A steel pipe is being carried down a hallway 9 ft wide. At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide. What is the length of the longest pipe that can be carried horizontally around the corner? 6 -- -
> Produce graphs of f that reveal all the important aspects of the curve. Estimate the intervals of increase and decrease and intervals of concavity, and use calculus to find these intervals exactly. 8 f(x) = 1 +-+
> Two vertical poles PQ and ST are secured by a rope PRS going from the top of the first pole to a point R on the ground between the poles and then to the top of the second pole as in the figure. Show that the shortest length of such a rope occurs when &Ic
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = tan x
> The frame for a kite is to be made from six pieces of wood. The four exterior pieces have been cut with the lengths indicated in the figure. To maximize the area of the kite, how long should the diagonal pieces be? b a a
> Find the dimensions of a rectangle with perimeter 100 m whose area is as large as possible.
> Let and be positive numbers. Find the length of the shortest line segment that is cut off by the first quadrant and passes through the point (a, b).
> The manager of a 100-unit apartment complex knows from experience that all units will be occupied if the rent is $800 per month. A market survey suggests that, on average, one additional unit will remain vacant for each $10 increase in rent. What rent sh
> A manufacturer has been selling 1000 television sets a week at $450 each. A market survey indicates that for each $10 rebate offered to the buyer, the number of sets sold will increase by 100 per week. (a). Find the demand function. (b). How large a reba
> During the summer months Terry makes and sells necklaces on the beach. Last summer he sold the necklaces for @10 each and his sales averaged 20 per day. When he increased the price by $1, he found that the average decreased by two sales per day. (a). Fin
> A baseball team plays in a stadium that holds 55,000 spectators. With ticket prices at $10, the average attendance had been 27,000. When ticket prices were lowered to $8, the average attendance rose to 33,000. (a). Find the demand function, assuming that
> (a). Show that if the profit P (x) is a maximum, then the marginal revenue equals the marginal cost. (b). If C (x) 16,000 + 500x – 1.6x2 + 0.004x3 is the cost function and p (x) = 1700 – 7x is the demand function, find the production level that will maxi
> (a). If C (x) is the cost of producing units of a commodity, then the average cost per unit is c (x) = C (x)/x. Show that if the average cost is a minimum, then the marginal cost equals the average cost. (b). If C (x) = 16,000 + 200x + 4x3/2, in dollars,
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = r - x
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. x² – 1 f(x):
> At which points on the curve y = 1 + 40x3 – 3x5 does the tangent line have the largest slope?
> The sum of two positive numbers is 16. What is the smallest possible value of the sum of their squares?
> Find an equation of the line through the point (3, 5) that cuts off the least area from the first quadrant.
> A woman at a point A on the shore of a circular lake with radius 2 mi wants to arrive at the point C diametrically opposite A on the other side of the lake in the shortest possible time (see the figure). She can walk at the rate of 4 mi/h and row a boat
> Given that which of the following limits are indeterminate forms? For those that are not an indeterminate form, evaluate the limit where possible. lim f(x) = 0 lim g(x) = 0 lim h(x) = 1 %3D エ→ エ→ロ lim p(x) = 0 lim q(x) = 0 %3D f(x) (a) lim g(x) 1-a
> Suppose the refinery in Exercise 35 is located 1 km north of the river. Where should P be located? Exercise 35: An oil refinery is located on the north bank of a straight river that is 2 km wide. A pipeline is to be constructed from the refinery to sto
> An oil refinery is located on the north bank of a straight river that is 2 km wide. A pipeline is to be constructed from the refinery to storage tanks located on the south bank of the river 6 km east of the refinery. The cost of laying pipe is $400,000/k
> A boat leaves a dock at 2:00 PM and travels due south at a speed of 20 km/h. Another boat has been heading due east at 15 km/h and reaches the same dock at 3:00 PM. At what time were the two boats closest together?
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> The graph shows the fuel consumption of a car (measured in gallons per hour) as a function of the speed of the car. At very low speeds the engine runs inefficiently, so initially decreases as the speed increases. But at high speeds the fuel consumption i
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = x – 1
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> Describe how the graph of f varies as varies. Graph several members of the family to illustrate the trends that you discover. In particular, you should investigate how maximum and minimum points and inflection points move when c changes. You should also
> The family of functions f (t) = C (e-at – e-bt), where a, b, and C are positive numbers and b > a, has been used to model the concentration of a drug injected into the bloodstream at time t = 0. Graph several members of this family. What do they have in
> Investigate the family of curves given by the parametric equations x= t3 - ct, y =t2. In particular, determine the values of for which there is a loop and find the point where the curve intersects itself. What happens to the loop as c increases? Find the
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. At what points does the curve have vertical or horizontal tangents? x = t* + 41 – 81?, y= 2t2 – t
> Graph the curve in a viewing rectangle that displays all the important aspects of the curve. At what points does the curve have vertical or horizontal tangents? x = t* – 2t° – 2t', y=r°- t
> Use a graph to estimate the coordinates of the leftmost point on the curve x = t4 – t2, y = t + ln t. Then use calculus to find the exact coordinates.
> In Example 4 we considered a member of the family of functions f (x) = sin (x + sin cs) that occur in FM synthesis. Here we investigate the function with c = 3. Start by graphing f in the viewing rectangle [0, π] by [-1.2, 1.2]. How many local maximum po
> Graph f (x) = ex + ln |x – 4| using as many viewing rectangles as you need to depict the true nature of the function.
> Produce graphs of f that reveal all the important aspects of the curve. In particular, you should use graphs of f' and f" to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. f(x) = x° –
> Use a computer algebra system to graph f and to find f' and f". Use graphs of these derivatives to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points of, f. 1- elz 1+ el f(x) = %3D
> Use a computer algebra system to graph f and to find f' and f". Use graphs of these derivatives to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points of, f. f(x) = (x² – 1)e' arctan x
> In this project we investigate the most economical shape for a can. We first interpret this to mean that the volume V of a cylindrical can is given and we need to find the height and radius that minimize the cost of the metal to make the can (see the fig
> Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why.

