Question: Use a graph to estimate the x-
Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the -axis the region enclosed by these curves.
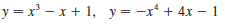
Transcribed Image Text:
y = x' – x + 1, y= -x* + 4x – 1
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x = (y – 3)', x = 4; about y = 1
> Find the total length of the astroid x = a cos3θ, y = sin3θ, where a > 0.
> Find the average value of the function on the given interval. g(x) = x, [1,8]
> Find the interval [a, b] for which the value of the integral fba (2 + x – x2) dx is a maximum.
> Let I = f40 f(x) dx, where f is the function whose graph is shown. (a). Use the graph to find L2, R2, and M2. (b). Are these underestimates or overestimates of I? (c). Use the graph to find T2. How does it compare with I? (d). For any value of n, list
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y = -x² + 6x – 8, y = 0; about the y-axis
> A hawk flying at 15m/s at an altitude of 180 m accidentally drops its prey. The parabolic trajectory of the falling prey is described by the equation y = 180 – x2/45 until it hits the ground, where is its height above the ground and is the horizontal dis
> Use either a CAS or a table of integrals to find the exact length of the curve. y = In x, 1<xs3
> f (x) = 2x/ (1 + x2)2, [0, 2] (a). Find the average value of f on the given interval. (b). Find such that fave = f (c). (c). Sketch the graph of f and a rectangle whose area is the same as the area under the graph of f.
> Find the average value of the function on the given interval. fa) — 4х — х, [О, 4]
> Find the exact length of the curve. x = y3/2, 0 < y < 1
> Find the exact length of the curve. y2 = 4 (x + 4)3, 0 < x < 2, y > 0
> Find the exact length of the curve. x = 1 + 3t2, y = 4 + 2t3, 0 < t < 1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x = t cos t, y =t sin t, 0 st< 27 0 <t< 27
> The figure shows a region consisting of all points inside a square that are closer to the center than to the sides of the square. Find the area of the region. 2. 2. 2.
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x =t + cos t, y=t- sin t, 0st< 2m
> Let f (x) = 0 if is any rational number and f (x) = 1 if is any irrational number. Show that f is not integrable on [0, 1].
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x= y? – 2y, 0 <y<2
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. y = sin x, 0<x<T
> If the region shown in the figure is rotated about the y-axis to form a solid, use Simpson’s Rule with n = 10 to estimate the volume of the solid. y 5 4 1 1 2 3 4 5 6 7 8 9 10 11 12 í 3. 2.
> Use Simpson’s Rule with n = 10 to estimate the volume obtained by rotating about the y-axis the region under the curve y = √1 + x3, 0 < x < 1.
> Find the length of the loop of the curve x = 3t – t3, y = 3t2.
> (a). In Example 2 in Section 1.7 we showed that the parametric equations x = cos t, y = sin t, 0 < t < 2π, represent the unit circle. Use these equations to show that the length of the unit circle has the expected value. (b). In Example 3 in Section 1.7
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by your calculator. x = sin t, y = 1?, 0 st< 2n
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by your calculator. y = xe, 0<I<5
> Sketch the region in the plane consisting of all points (x, y) such that 2xy < |x – y|< x? + y?
> Graph the curve and find its exact length. x = et + e-t, y = 5 – 2t, 0 < t < 3
> Graph the curve and find its exact length. x = et cos t, y = et sin t, 0 < t < π
> On May 7, 1992, the space shuttle Endeavour was launched on mission STS-49, the purpose of which was to install a new perigee kick motor in an Intelsat communications satellite. The table gives the velocity data for the shuttle between liftoff and the je
> Graph the curve and find its exact length. y = x3/3 + 1/4x, 1 < x < 2
> Graph the curve and find its exact length. x = et – t, y = 4et/2, -8 < t < 3
> Find the exact length of the curve. x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ), 0 < θ < π
> Find the exact length of the curve. y = 1/4x2 – 1/2 lnx, 1 < x < 2
> Find the exact length of the curve. y = √x – x2 + sin-1 (√x)
> Use the arc length formula (2) to find the length of the curve y – 2x - 5, -1 < x < 3. Check your answer by noting that the curve is a line segment and calculating its length by the distance formula.
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. х%3D1+y;, х30, у%31, у%3D2
> A cone of radius r centimeters and height h centimeters is lowered point first at a rate of 1 cm/s into a tall cylinder of radius R centimeters that is partially filled with water. How fast is the water level rising at the instant the cone is completely
> Let V be the volume of the solid obtained by rotating about the y-axis the region bounded by y = √x and y = x2. Find V both by slicing and by cylindrical shells. In both cases draw a diagram to explain your method.
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. Sketch the region and a typical shell. y = 4(x – 2), y =x² – 4x + 7
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. Sketch the region and a typical shell. y = 3 + 2x – x², x+ y = 3
> Economists use a cumulative distribution called a Lorenz curve to describe the distribution of income between households in a given country. Typically, a Lorenz curve is defined on [0, 1] with endpoints (0, 0) and (1, 1), and is continuous, increasing, a
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. Sketch the region and a typical shell. y = e*, y = 0, x= 0, x= 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. Sketch the region and a typical shell. y = x², y = 0, x= 1
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x² + (y – 1)? = 1; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y = -x? + 6x – 8, y = 0; about the x-axis
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. Sketch the region and a typical shell. у%3D 1/х, у—0, х— 1, х—2
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x'sin x, y = 0, 0 <x< T; about x = -1
> Given a sphere with radius r, find the height of a pyramid of minimum volume whose base is a square and whose base and triangular face are all tangent to the sphere. What if the base of the pyramid is a regular n-gon? (A regular n-gon is a polygon with e
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = sin?x, y = sin*x, 0 <x< T; about x = T/2
> Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the -axis the region enclosed by these curves.
> Each integral represents the volume of a solid. Describe the solid. y dy 1+ y* (a) 27 (b) * 27 (7 – x)(cos x – sin x) dx
> Explain exactly what is meant by the statement that “differentiation and integration are inverse processes.”
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. y = e*, y = 0, x = 0, x = 4; about x= 5
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = 1- x², y = 0; about the x-axis
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. x = /sin y, 0 sy<T, I= 0; about y = 4
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell. y = x', x = y?; about y = -1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell. y = x', y = 0, x= 1; about y = 1
> ABCD is a square piece of paper with sides of length 1 m. A quarter-circle is drawn from B to D with center A. The piece of paper is folded along EF, with E on AB and A on AD, so that A falls on the quarter-circle. Determine the maximum and minimum areas
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell. у 3х, у —2 — х?; about x — 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell. у%3D 4х — х, у — 3; about x %31
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell.
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. Sketch the region and a typical shell. y = x', y = 0, x = 1; about x = 2
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x+у-3, х%4- (у — 1)2
> (a). Use six rectangles to find estimates of each type for the area under the given graph of f from x = 0 to x = 12. (i). L6 (sample points are left endpoints) (ii). R6 (sample points are right endpoints) (iii). M6 (sample points are midpoints) (b). Is L
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x= 1+ (y – 2), x=2
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x= Vỹ, x= 0, y=1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у%3D2 — х, у — 0, х — 1, х — 2;B about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = x, y = Vr; about y = 1
> For what values of is there a straight line that intersects the curve in four distinct points? Y = x4 + cx3 + 12x2 – 5x + 2
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y =x', x = 2, y = 0; about the y-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y? = x, x = 2y; about the y-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = ¿r², y = 5 – x²; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = x', y = x, x> 0; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = In x, y = 1, y = 2, x= 0; about the y-axis
> Find the volume of the described solid S. A tetrahedron with three mutually perpendicular faces and three mutually perpendicular edges with lengths 3 cm, 4 cm, and 5 cm
> Show that if a > -1 and b > a + 1, then the following integral is convergent. dx Jo 1+ x*
> Graph the astroid x = a cos3θ, y = a sin3θ and set up an integral for the area that it encloses. Then use a computer algebra system to evaluate the integral.
> Find the volume of the described solid S. A frustum of a pyramid with square base of side b, square top of side a, and height h. a b
> Find the volume of the described solid S. A cap of a sphere with radius r and heigh h. h
> For what values of does the curve y = cx3 + ex have inflection points?
> Investigate the family of functions f (x) = ln (sinx + C). What features do the members of this family have in common? How do they differ? For which values of C is f continuous on (-∞, ∞)? For which values of C does f have no graph at all? What happens a
> Find the volume of the described solid S. A frustum of a right circular cone with height h, lower base radius R, and top radius r. -r- h R
> Find the volume of the described solid S. A right circular cone with height h and base radius r.
> (a). A model for the shape of a bird’s egg is obtained by rotating about the -axis the region under the graph of Use a CAS to find the volume of such an egg. (b). For a Red-throated Loon, a = -0.06, b = 0.04, c = 0.1, and d = 0.54. Gr
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. x = 2/y, x= 0, y = 9; about the y-axis %3D
> (a). If the region shown in the figure is rotated about the x-axis to form a solid, use Simpson’s Rule with n = 8 to estimate the volume of the solid. (b). Estimate the volume if the region is rotated about the y-axis. Use Simpson&aci
> A log 10 m long is cut at 1-meter intervals and its cross-sectional areas A (at a distance from the end of the log) are listed in the table. Use the Midpoint Rule with n = 5 to estimate the volume of the log. x (m) A (m²) x (m) A (m²) 0.68 6. 0.53 1
> A CAT scan produces equally spaced cross-sectional views of a human organ that provide information about the organ otherwise obtained only by surgery. Suppose that a CAT scan of a human liver shows cross-sections spaced 1.5 cm apart. The liver is 15 cm l
> Suppose f is continuous on [0, ∞] and limx→∞f (x) = 1. Is it possible that f∞0f (x) dx is convergent?
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A heavy rope, 50 ft long, weighs 0.5 lb/ft and hangs over the edge of a building 120 ft high. (a). How much work is done in pulling the rope
> Each integral represents the volume of a solid. Describe the solid. (a) 7 y dy (b) 7 [(1 (1 + cos x)? – 1°]dx
> For any number c, we let fc (x) be the smaller of the two numbers (x – c)2 and (x – c – 2)2. Then we define Find the maximum and minimum values of g (c) if -2 g(c) f.(x)dx
> Each integral represents the volume of a solid. Describe the solid. *w/2 (а) т cos?x dx (b) (y* – y*) dy
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x, y = xel-/2, about y = 3
> Use a graph to find approximate -coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the -axis the region bounded by these curves. y = 3 s
> Use a graph to find approximate -coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the -axis the region bounded by these curves. y = 2 +
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = cos x, y = 2 – cos x, 0<I< 27; about y 4
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. x² – y? = 1, x= 3; about x = -2
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. y = x', y = Vx; about y = 1
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. y = x', y = Vx; about x = 1

