Question: Use a Riemann sum with n = 4
Use a Riemann sum with n = 4 and left endpoints to estimate the area under the graph in Fig. 1 for 0 ≤ x ≤ 2.
Figure 1:
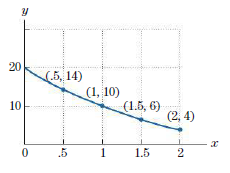
Transcribed Image Text:
20 10 ม 0 (.5, 14) .5 (1, 10) 1 (1.5, 6) 1.5 (2,4) 2
> Figure 4 shows the graphs of several functions f (x) for which f (x) = 2/x. Find the expression for the function f ‘(x) whose graph passes through (1, 2). Figure 4: (1, 2) 6 4 2 y -2. -4- 4 6 + 8 | | | 10 12 X
> Find all functions f (x) that satisfy the given conditions. f ‘(x) = x2 + √x, f (1) = 3
> Find all functions f (x) that satisfy the given conditions. f ‘(x) = √x + 1, f (4) = 0
> Find all functions f (x) that satisfy the given conditions. f ‘ (x) = 8x1/3, f (1) = 4
> Find all functions f (x) that satisfy the given conditions. f ‘(x) = x, f (0) = 3
> Find all functions f (x) that satisfy the given conditions. f ‘(x) = 2x - e-x, f (0) = 1
> Find all functions f (x) that satisfy the given conditions. f ‘(x) = .5e-0.2x, f (0) = 0
> Find all functions f (t) that satisfy the given condition. f ‘(t) = t2 - 5t - 7
> Find all antiderivatives of each following function: f (x) = e-3x
> Find all functions f (t) that satisfy the given condition. f ‘(t) = 0
> Find all functions f (t) that satisfy the given condition. f ‘(t) = 4/(6 + t)
> Find all functions f (t) that satisfy the given condition. f ‘(t) = t3/2
> Find the value of k that makes the antidifferentiation formula true. ∫5/(2 - 3x) dx = k ln |2 - 3x| + C
> Find the value of k that makes the antidifferentiation formula true. ∫3/(2 + x) dx = k ln |2 + x| + C
> Calculate the following integrals. ∫ (x3 + 3x2 - 1)dx
> Calculate the following integrals. ∫ 2/(x + 4) dx
> Calculate the following integrals. ∫ 2x + 1 dx
> Calculate the following integrals. ∫ (x2 - 3x + 2) dx
> Calculate the following integrals. ∫32 dx
> Generalize the result of Exercise 73 as follows: Let n be a positive integer. Show that 0∫1 (n√x – xn) dx = (n-1)/(n+1).
> Find the value of k that makes the antidifferentiation formula true. ∫ (2x - 1)3 dx = k(2x - 1)4 + C
> Show that 0∫1 (√x - x2) dx = 1/3.
> Generalize the result of Exercise 71 as follows: Let n be a positive integer. Show that for any positive number b we have 0∫bn n√x dx + 0∫b xn dx = bn+1
> Show that for any positive number b we have 0∫b2 √x dx + 0∫b x2 dx = b3
> For what value of a is the shaded area in Fig. 4 equal to 1? Figure 4: y = r ย 0 D a, a
> Find a function f (x) whose graph goes through the point (1, 1) and whose slope at any point (x, f (x)) is 3x2 - 2x + 1.
> If money is deposited steadily in a savings account at the rate of $4500 per year, determine the balance at the end of 1 year if the account pays 9% interest compounded continuously.
> The annual world rate of water use t years after 1960, for t ≤ 35, was approximately 860 e0.04t cubic kilometers per year. How much water was used between 1960 and 1995?
> Suppose that water is flowing into a tank at a rate of r (t) gallons per hour, where the rate depends on the time t according to the formula r (t) = 20 - 4t, 0 ≤ t ≤ 5. (a) Consider a brief period of time, say, from t1 to t2. The length of this time peri
> True or false: If 3 ≤ f (x) ≤ 4 whenever 0 ≤ x ≤ 5, then 3 ≤ 1/5 0∫5 f (x) dx ≤ 4.
> In Fig. 3, the rectangle has the same area as the region under the graph of f (x). What is the average value of f (x) on the interval 2 ≤ x ≤ 6? Figure 3: fi 0 2 6 x y 0 y = f(x) 2 6
> Find the value of k that makes the antidifferentiation formula true. ∫ (3x + 2)4 dx = k(3x + 2)5 + C
> What number does the sum [13 + (1 + 1/n)3 + (1 + 2/n)3+ (1 + 3/n)3+ … + (1 + n-1/n)3] * 1/n approach as n gets very large?
> What number does [e0 + e1/n + e2/n + e3/n + … + e(n-1)/n] * 1/n approach as n gets very large?
> Suppose that the interval 0 ≤ t ≤ 3 is divided into 1000 subintervals of width Δt. Let t1, t2, … , t1000 denote the right endpoints of these subintervals. If we need to estimate the
> For each number x satisfying -1 … x … 1, define h(x) by h(x) = -1∫x √ (1 - t2) dt. (a) Give a geometric interpretation of the values h(0) and h(1). (b) Find the derivative h ‘(x).
> Let x be any positive number, and define g(x) to be the number determined by the definite integral g(x) = 0∫x 1/(1 + t2) dt. (a) Give a geometric interpretation of the number g(3). (b) Find the derivative g ‘ (x).
> A retail store sells a certain product at the rate of g(t) units per week at time t, where g(t) = rt. At time t = 0, the store has Q units of the product in inventory. (a) Find a formula f (t) for the amount of product in inventory at time t. (b) Determi
> A store has an inventory of Q units of a certain product at time t = 0. The store sells the product at the steady rate of Q/A units per week and exhausts the inventory in A weeks. (a) Find a formula f (t) for the amount of product in inventory at time t.
> Find the volume of the solid of revolution generated by revolving about the x-axis the region under the curve y = 1 - x2 from x = 0 to x = 1.
> In Fig. 2, three regions are labeled with their areas. Determine a∫c f (x) dx and determine a∫d f (x) dx. Figure 2: y a .68 b .42 1.7 d
> Suppose that the interval 0 ≤ x ≤ 1 is divided into 100 subintervals with a width of Δx = .01. Show that the sum [3e-0.01] Δx + [3e-0.02] Δx + [3e-0.03] Δx + … + [3e-1] Δx is close to 3(1 - e-1).
> Find the value of k that makes the antidifferentiation formula true. ∫7/(8 - x)4 dx = k/(8 - x)3 + C
> Find the average value of f (x) = 1/x3 from x = 1/3 to x = 1/2.
> Three thousand dollars is deposited in the bank at 4% interest compounded continuously. What will be the average value of the money in the account during the next 10 years?
> Find the consumers’ surplus for the demand curve p = √(25 - .04x) at the sales level x = 400.
> Use a Riemann sum with n = 5 and midpoints to estimate the area under the graph of f (x) = e2x on the interval 0 ≤ x ≤ 1. Then, use a definite integral to find the exact value of the area to five decimal places.
> Use a Riemann sum with n = 2 and midpoints to estimate the area under the graph of f (x) = 1/(x + 2) on the interval 0 ≤ x ≤ 2. Then, use a definite integral to find the exact value of the area to five decimal places.
> Redo Exercise 47 using right endpoints. Exercise 47: Use a Riemann sum with n = 4 and left endpoints to estimate the area under the graph in Fig. 1 for 0 ≤ x ≤ 2. Figure 1: 20 10 ม 0 (.5, 14) .5 (1, 10) 1 (1.
> A rock thrown straight up into the air has a velocity of υ(t) = -9.8t + 20 meters per second after t seconds. (a) Determine the distance the rock travels during the first 2 seconds. (b) Represent the answer to part (a) as an area.
> A drug is injected into a patient at the rate of f (t) cubic centimeters per minute at time t. What does the area under the graph of y = f (t) from t = 0 to t = 4 represent?
> If the marginal revenue function for a company is 400 - 3x2, find the additional revenue received from doubling production if 10 units are currently being produced.
> Find the value of k that makes the antidifferentiation formula true. ∫ (4 - x)-1 dx = k ln |4 – x| + C
> An airplane tire plant finds that its marginal cost of producing tires is .04x + $150 at a production level of x tires per day. If fixed costs are $500 per day, find the cost of producing x tires per day.
> Let k be a constant, and let y = f (t) be a function such that y ’ = kty. Show that y = Cekt2/2, for some constant C.
> Describe all solutions of the following differential equations, where y represents a function of t. (a) y ’ = 4t (b) y ’ = 4y (c) y ’ = e4t
> Find the function f (x) for which f ‘(x) = e-5x, f (0) = 1.
> Find the function f (x) for which f ‘ (x) = (x - 5)2, f (8) = 2.
> Find the area of the region between the curves y = 2x2 + x and y = x2 + 2 from x = 0 to x = 2.
> Find the area of the region bounded by the curves y = x3 - 3x + 1 and y = x + 1.
> Find the area of the shaded region. -2 ม y = 2 – 2 – in 3
> Find the area of the shaded region. Y 0 y=e² - ex 1
> Find the area of the shaded region. Y 0 1/2 y=x²-x-1 y = 1-1/x 1 2
> Find the value of k that makes the antidifferentiation formula true. ∫√(x + 1) dx = k(x + 1)3/2 + C
> Find all antiderivatives of each following function: f (x) = e3x
> Find the area of the shaded region. 4 0 y=4-2² 1 y=1-x² 2
> Find the area of the shaded region. 1.21 3 = fi X} = f 0 "
> Find the area of the shaded region. y=e-z Y 0 1 y=e² In 2 1
> Find the area of the shaded region. -2 =R Y 0 y = x³ + 2x 2
> Find the area of the shaded region. x x=k xt = f 0 fi
> Find the area under the curve y = 1 + √x from x = 1 to x = 9.
> Find the area under the curve y = (3x - 2)-3 from x = 1 to x = 2.
> Calculate the following integrals. 0∫1 (3 + e2x)/ex dx
> Calculate the following integrals. 0∫ln 3 (ex + e-x)/ e2x dx
> Calculate the following integrals. ln 2∫ln 3 (ex + e-x) dx
> Find the value of k that makes the antidifferentiation formula true. ∫ (5x - 7)-2 dx = k(5x - 7)-1 + C
> Calculate the following integrals. 0∫ln 2 (ex - e-x) dx
> Calculate the following integrals. -2∫2 3/2e3x dx
> Calculate the following integrals. 0∫5 (5 + 3x)-1 dx
> Calculate the following integrals. 3∫6 e2-(x/3) dx
> Calculate the following integrals. 1∫4 1/x2 dx
> Calculate the following integrals. 2/3 0∫8 √ (x + 1) dx
> Calculate the following integrals. 1∫24/x5 dx
> Calculate the following integrals. 0∫1 [2/(x + 1) – 1/(x + 4)] dx
> Calculate the following integrals. -1∫2 √ (2x + 4) dx
> Calculate the following integrals. 0∫1/8 5√x dx
> Find the value of k that makes the antidifferentiation formula true. ∫4 e3x+1 dx = k e3x+1 + C
> Calculate the following integrals. -1∫1 (x + 1)2 dx
> Calculate the following integrals. ∫ (5/x – x/5) dx
> Calculate the following integrals. ∫ √(4 – x) dx
> Calculate the following integrals. ∫ (2x + 3)7 dx
> Calculate the following integrals. ∫ (3x4 - 4x3) dx
> Calculate the following integrals. ∫5/√(x – 7) dx
> Calculate the following integrals. ∫ e-x/2 dx
> Calculate the following integrals. ∫ 5√(x + 3) dx
> What is a Riemann sum?
> In the formula Δx = (b – a)/n, what do a, b, n, and Δx denote?
> Find the value of k that makes the antidifferentiation formula true. ∫2e4x-1 dx = ke4x-1 + C
> State the formula for 1h(x)dx for each of the following functions. (a) h(x)xr, r ≠ -1 (b) h(x) = ekx (c) h(x) = 1/x (d) h(x) = f (x) + g(x) (e) h(x) = kf (x)
> What does it mean to anti-differentiate a function?

