Question: Use Exercise 22 to find the centroid
Use Exercise 22 to find the centroid of the triangle with vertices (0, 0), (a, 0), and (a, b), where a > 0 and b > 0.
Exercise 22:
Let D be a region bounded by a simple closed path C in the xy-plane. Use Green’s Theorem to prove that the coordinates of the centroid (x, y) of D are
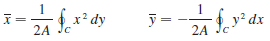
where A is the area of D.
Transcribed Image Text:
x² dy I= 2A Jc 2A
> How do you use power series to solve a differential equation?
> Evaluate the line integral, where C is the given curve. ∫C (x2 + y2 + z2) ds, C: x = t, y = cos 2t, z = sin 2t, 0 < t < π2
> Evaluate the line integral, where C is the given curve. ∫C xeyz ds, C is the line segment from (0, 0, 0) to (1, 2, 3)
> Evaluate the line integral, where C is the given curve. ∫C y2z ds, C is the line segment from (3, 1, 2) to (1, 2, 5)
> If C is a smooth curve given by a vector function r (t), a (v• dr = v · [r(b) – r(a)]
> Evaluate the line integral, where C is the given curve. ∫C y ds, C: x − t2, y = 2t, 0 < t < 3
> A 160-lb man carries a 25-lb can of paint up a helical staircase that encircles a silo with a radius of 20 ft. If the silo is 90 ft high and the man makes exactly three complete revolutions climbing to the top, how much work is done by the man against gr
> An object with mass m moves with position function r(t) = a sin t i + b cos t j + ct k, 0 < t < y2. Find the work done on the object during this time period.
> The position of an object with mass m at time t is r(t) = at2 i + bt3 j, 0 < t < 1. (a). What is the force acting on the object at time t? (b). What is the work done by the force during the time interval 0 < t < 1?
> The force exerted by an electric charge at the origin on a charged particle at a point (x, y, z) with position vector r = 〈x, y, z〉 is F (r) = Kr/|r |3 where K is a constant. (See Example 16.1.5.) Find the work done as the particle moves along a straight
> Find the work done by the force field F (x, y, z) = 〈x - y^2, y - z^2, z - x^2 〉 on a particle that moves along the line segment from (0, 0, 1) to (2, 1, 0).
> Evaluate the line integral. ∫C y3 dx + x2 dy, C is the arc of the parabola x = 1 - y2 from (0, -1) to (0, 1)
> Find the work done by the force field F (x, y) = x2 i + yex j on a particle that moves along the parabola x = y2 + 1 from (1, 0) to (2, 1).
> We have seen that all vector fields of the form F = ∇g satisfy the equation curl F = 0 and that all vector fields of the form F = curl G satisfy the equation div F = 0 (assuming continuity of the appropriate partial derivatives). This suggests the questi
> If a wire with linear density ρ (x, y, z) lies along a space curve C, its moments of inertia about the x-, y-, and z-axes are defined as Find the moments of inertia for the wire in Exercise 35. Exercise 35: (a). Write the formulas similar
> This exercise demonstrates a connection between the curl vector and rotations. Let B be a rigid body rotating about the z-axis. The rotation can be described by the vector w − k, where is the angular speed of B, that is, the tangential
> Use Green’s first identity to show that if f is harmonic on D, and if f (x, y) = 0 on the boundary curve C, then ∫∫D |∇f |2 dA = 0. (Assume the same hypotheses as in Exercise 33.)
> Recall from Section 14.3 that a function t is called harmonic on D if it satisfies Laplace’s equation, that is, ∇2g = 0 on D. Use Green’s first identity (with the same hypotheses as in Exercise 33) to
> Use Green’s first identity (Exercise 33) to prove Green’s second identity: first identity: where D and C satisfy the hypotheses of Green’s Theorem and the appropriate partial derivatives of f and
> Let r = x i + y j + z k and r = |r |. If F = r/rp, find div F. Is there a value of p for which div F = 0?
> Let r = x i + y j + z k and r = |r |. Verify each identity. (a). = r = 3 (b). = ∙ (r r) = 4r (c). ∇2r3 = 12r
> Show that if the vector field F = P i + Q j + R k is conservative and P, Q, R have continuous first-order partial derivatives, then aP aR aR ду ax az ax dz ду
> Evaluate the line integral. ∫C y dx + (x + y2) dy, C is the ellipse 4x2 + 9y2 = 36 with counterclockwise orientation
> Prove the identity, assuming that the appropriate partial derivatives exist and are continuous. If f is a scalar field and F, G are vector fields, then f F, F ∙ G, and F × G are defined by div (f F) = f div F + F â&
> Prove the identity, assuming that the appropriate partial derivatives exist and are continuous. If f is a scalar field and F, G are vector fields, then f F, F ∙ G, and F × G are defined by div (F + G) = div F + div G
> Show that any vector field of the form F (x, y, z) = f (x) i + g (y) j + h (z) k where f, t, h are differentiable functions, is irrotational.
> Is there a vector field G on R3 such that curl G =〈x, y, z〉? Explain.
> Is there a vector field G on R3 such that curl G =〈x sin y, cos y, z - xy〉? Explain.
> Use Green’s Theorem to evaluate the line integral along the given positively oriented curve. ∫C y4 dx + 2xy3 dy, C is the ellipse x2 + 2y2 = 2
> Use Green’s Theorem to evaluate the line integral along the given positively oriented curve. ∫C (y + e^√x) dx + (2x + cos y2) dy, C is the boundary of the region enclosed by the parabolas y = x2 and x = y2
> Use Green’s Theorem to evaluate the line integral along the given positively oriented curve. ∫C (x2 + y2) dx + (x2 - y2) dy, C is the triangle with vertices (0, 0), (2, 1), and (0, 1)
> Use Green’s Theorem to evaluate the line integral along the given positively oriented curve. ∫C yex dx + 2ex dy, C is the rectangle with vertices (0, 0), (3, 0), (3, 4), and (0, 4)
> Evaluate the line integral by two methods: (a) directly and (b) using Green’s Theorem. ∮C x2y2 dx 1 xy dy, C consists of the arc of the parabola y = x2 from (0, 0) to (1, 1) and the line segments from (1, 1) to (0, 1) and from (0, 1) to (0, 0)
> Evaluate the line integral. ∫C yz cos x ds, C: x = t, y = 3 cos t, z = 3 sin t, 0 < t < π
> Find the work done by the force field F (x, y) = x i + (y + 2) j in moving an object along an arch of the cycloid r(t) = (t - sin t) i + (1 - cos t) j 0 < t < 2 π
> If a wire with linear density ρ (x, y) lies along a plane curve C, its moments of inertia about the x- and y-axes are defined as Find the moments of inertia for the wire in Example 3. -[v°ptx, y) ds I, = x°p(x, y) ds
> Find the mass and center of mass of a wire in the shape of the helix x = t, y = cos t, z = sin t, 0 < t < 2 π, if the density at any point is equal to the square of the distance from the origin.
> (a). Write the formulas similar to Equations 4 for the center of mass (z ̅, y ̅, z ̅) of a thin wire in the shape of a space curve C if the wire has density function ρ (x, y, z). (b). Find the center of mass of a wire in the shape of the helix x = 2 sin
> A thin wire has the shape of the first-quadrant part of the circle with center the origin and radius a. If the density function is ρ (x, y) = kxy, find the mass and center of mass of the wire.
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y) = 0.3 i - 0.4 j ZA
> Match the functions f with the plots of their gradient vector fields labeled I–IV. Give reasons for your choices. f (x, y) = sin √ (x^2 + y^2) IV 4 -4 4 سر ه م -4
> What does Clairaut’s Theorem say?
> Complete the proof of the special case of Green’s Theorem by proving Equation 3.
> Evaluate the line integral by two methods: (a) directly and (b) using Green’s Theorem. ∮C xy dx + x2y3 dy, C is the triangle with vertices (0, 0), (1, 0), and (1, 2)
> If F and G are vector fields whose component functions have continuous first partial derivatives, show that curl (F × G) = F div G - G div F + (G ∙ ∇) F – (F ∙∇) G
> Calculate ∫C F ∙ dr, where F (x, y) = 〈x2 + y, 3x - y2〉 and C is the positively oriented boundary curve of a region D that has area 6.
> Plot the gradient vector field of f together with a contour map of f. Explain how they are related to each other. f (x, y) = ln (1 + x2 + 2y2)
> Use Exercise 25 to find the moment of inertia of a circular disk of radius a with constant density ρ about a diameter. (Compare with Example 15.4.4.) Exercise 25: A plane lamina with constant density ρ (x, y) = ρ occupi
> A plane lamina with constant density ρ (x, y) = ρ occupies a region in the xy-plane bounded by a simple closed path C. Show that its moments of inertia about the axes are 1, = x* dy dx 3 3 Jc
> Use Exercise 22 to find the centroid of a quarter-circular region of radius a. Exercise 22: Let D be a region bounded by a simple closed path C in the xy-plane. Use Green’s Theorem to prove that the coordinates of the centroid (x, y)
> Let D be a region bounded by a simple closed path C in the xy-plane. Use Green’s Theorem to prove that the coordinates of the centroid (x, y) of D are where A is the area of D. x² dy I= 2A Jc 2A
> Suppose you’re asked to determine the curve that requires the least work for a force field F to move a particle from one point to another point. You decide to check first whether F is conservative, and indeed it turns out that it is. How would you reply
> If a circle C with radius 1 rolls along the outside of the circle x2 + y2 = 16, a fixed point P on C traces out a curve called an epicycloid, with parametric equations x = 5 cos t - cos 5t, y = 5 sin t - sin 5t. Graph the epicycloid and use (5) to find t
> Evaluate the line integral by two methods: (a) directly and (b) using Green’s Theorem. ∮C y dx - x dy, C is the circle with center the origin and radius 4
> Show that there is no vector field G such that curl G = 2x i + 3yz j - xz2 k
> Show that the line integral is independent of path and evaluate the integral. ∫C 2xe-y dx + (2y - x2e-y) dy, C is any path from (1, 0) to (2, 1)
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F (x, y, z) = yz i + xz j + (xy + 2z) k, C is the line segment from (1, 0, -2) to (4, 6, 3)
> Use Green’s Theorem to evaluate ∫C F ∙ dr. (Check the orientation of the curve before applying the theorem.) F (x, y) =〈√ (x^2 + 1), tan^ (-1) x〉, C is the triangle from (0, 0) to (1, 1) to (0, 1) to (0, 0)
> Evaluate the line integral by two methods: (a) directly and (b) using Green’s Theorem. ∮C y2 dx + x2y dy, C is the rectangle with vertices (0, 0), (5, 0), (5, 4), and (0, 4)
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (y2 cos x + cos y) i + (2y sin x - x sin y) j
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (2xy + y-2) i + (x2 - 2xy-3) j, y > 0
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (yex + sin y) i + (ex + x cos y) j
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = yex i + (ex + ey) j
> Let f be a joint density function of a pair of continuous random variables X and Y. (a). Write a double integral for the probability that X lies between a and b and Y lies between c and d. (b). What properties does f possess? (c). What are the expected v
> If a lamina occupies a plane region D and has density function ρ (x, y), write expressions for each of the following in terms of double integrals. (a). The mass (b). The moments about the axes (c). The center of mass (d). The moments of inertia about the
> Find curl F and div F if F (x, y, z) = e-x sin y i + e-y sin z j + e-z sin x k
> How do you find the length of a space curve given by a vector function r (t)?
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (xy + y2) i + (x2 + 2xy) j
> (a). What is the definition of curvature? (b). Write a formula for curvature in terms of r'(t) and T'(t). (c). Write a formula for curvature in terms of r'(t) and r''(t). (d). Write a formula for the curvature of a plane curve with equation y - f (x).
> Find the gradient vector field ∆f of f and sketch it. f (x, y) = 1/2 (x2 - y2)
> Find the gradient vector field ∆f of f and sketch it. f (x, y) = ½ (x – y)2
> Find the work done by the force field F in moving an object from P to Q. F (x, y) = (2x + y) i + x j; P (1, 1), Q (4, 3)
> Find the work done by the force field F in moving an object from P to Q. F (x, y) = x3 i + y3 j; P (1, 0), Q (2, 2)
> Suppose an experiment determines that the amount of work required for a force field F to move a particle from the point (1, 2) to the point (5, -3) along a curve C1 is 1.2 J and the work done by F in moving the particle along another curve C2 between the
> If u and v are differentiable vector functions, c is a scalar, and f is a real-valued function, write the rules for differentiating the following vector functions. (a). u (t) + v (t) (b). cu (t) (c). f (t) u (t) (d). u(t) ∙ v (t) (e). u (t) × v (t) (
> A table of values of a function f with continuous gradient is given. Find ∫C ∇f dr, where C has parametric equations x = t2 + 1 y = t3 + t 0 < t < 1
> Use Green’s Theorem to evaluate ∫C x2y dx - xy2 dy, where C is the circle x2 + y2 = 4 with counterclockwise orientation.
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F(x, y, z) = sin y i+ (x cos y + cos z)j – y sin z k, C: r(t) = sin ti + tj+ 2t k,
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F(x, y, z) = yze" i + e* j+ xye* k, C: r(t) = (t² + 1) i + (t² – 1) j + (r² - 21)
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F(x, y, z) = (y²z + 2xz²) i + 2xyz j + (xy² + 2x²z) k, C: x= Vī, y = t + 1, z = t²
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F (x, y) = (1 + xy) exy i + x2exy j, C: r (t) = cos t i + 2 sin t j, 0 < t < π/2
> (a) Find a function f such that F = ∆f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F (x, y) = x2y3 i + x3y2 j, C: r (t) =〈t3 - 2t, t3 + 2t〉, 0 < t < 1
> (a) Find a function f such that F = ∇f and (b) use part (a) to evaluate ∫C F ∙ dr along the given curve C. 12. F (x, y) = (3 + 2xy2) i + 2x2y j, C is the arc of the hyperbola y = 1/x from (1, 1) to (4, 1/4)
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y) = -1/2 i + (y – x) j ZA
> Determine whether or not F is a conservative vector field. If it is, find a function f such that F = ∇f. F (x, y) = (ln y + y/x) i + (ln x + x/y) j
> What is a vector function? How do you find its derivative and its integral?
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y) = 1/2 x i + y j ZA
> Use Green’s Theorem to evaluate ∫C √1 + x3 dx + 2xy dy where C is the triangle with vertices (0, 0), (1, 0), and (1, 3).
> Suppose a solid object occupies the region E and has density function ρ (x, y, z). Write expressions for each of the following. (a). The mass (b). The moments about the coordinate planes (c). The coordinates of the center of mass (d). The moments of iner
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y, z) = i ZA
> Write an expression for the area of a surface with equation z = f (x, y), (x, y) ∈ D.
> How do you find the tangent vector to a smooth curve at a point? How do you find the tangent line? The unit tangent vector?
> (a). What does it mean to say that f is continuous at (a, b)? (b). If f is continuous on R2, what can you say about its graph?
> Find the gradient vector field of f. f (x, y, z) = x2yey/z
> Find the gradient vector field of f. f (x, y, z) = √ (x^2 + y^2 + z^2)
> Find the gradient vector field of f. f (s, t) = √ (2s + 3t)
> Find the gradient vector field of f. f (x, y) = y sin (xy)
> What is the connection between vector functions and space curves?
> If a is a constant vector, r = x i + y j + z k, and S is an oriented, smooth surface with a simple, closed, smooth, positively oriented boundary curve C, show that Sf 2a · ds = (a x r) · dr 2а
> Sketch the vector field F by drawing a diagram like Figure 5 or Figure 9. Figure 9: F (x, y) = y i + (x + y) j ZA

