Question: Use the given information to determine the
Use the given information to determine the number of elements in each of the four disjoint subsets in the following Venn diagram.
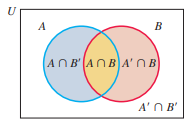
n(A′) = 30, n(B′) = 10, n(A′ ∪ B′) = 35, n(U) = 60
> If you paid $120 to a loan company for the use of $2,000 for 90 days, what annual rate of interest did they charge?
> How long will it take $5,000 to grow to $7,000 if it is invested at 6% compounded quarterly?
> A check for $3,097.50 was used to retire a 5-month $3,000 loan. What annual rate of interest was charged?
> What is the annual percentage yield (APY) for money invested at an annual rate of (A) 3.05% compounded quarterly? (B) 2.95% compounded continuously?
> A loan of $10,000 was repaid at the end of 6 months. What amount (principal and interest) was repaid, if a 6.5% annual rate of interest was charged?
> What is the annual percentage yield (APY) for money invested at an annual rate of (A) 4.32% compounded monthly? (B) 4.31% compounded daily?
> If a 50% annual rate is charged, how much interest will be owed on a loan of $1,000 for 30 days?
> If an investment earns 12% compounded continuously, how much should you deposit now to have $4,800 (A) 48 months from now? (B) 7 years from now?
> simplify each expression assuming that n is an integer and n ( 2.
> If $5,000 is loaned for 9 months at a 6.2% annual rate, how much interest is earned?
> If an investment company pays 8% compounded quarterly, how much should you deposit now to have $6,000 (A) 3 years from now? (B) 6 years from now?
> Discuss the similarities and differences in the graphs of future value A as a function of time t for loans of $400, $800, and $1,200, respectively, each at 7.5% simple interest (see the figure)
> If $2,000 is invested in an account that earns 8.25% compounded annually for 5 years, find the interest earned during each year and the amount in the account at the end of each year. Organize your results in a table.
> Solve each formula for the indicated variable. I = Prt; fort
> Discuss the similarities and differences in the graphs of future value A as a function of time t for loans of $4,000, $8,000, and $12,000, respectively, each at 7.5% compounded monthly for 8 years (see the figure).
> Solve each formula for the indicated variable. A = P + Prt; forr
> If $23,000 is invested at 13.5% compounded continuously, what is the amount after 15 years?
> Solve each formula for the indicated variable. I = Prt; forP
> If $20,000 is invested at 4% compounded monthly, what is the amount after (A) 5 years? (B) 8 years?
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> Solve two ways: (A) using a tree diagram, and (B) using the multiplication principle n how many ways can 3 coins turn up—heads H, or tails T—if combined outcomes such as (H, T, H), (H, H, T), and (T, H, H) are considered as different?
> Solve two ways: (A) using a tree diagram, and (B) using the multiplication principle How many 2-letter code words can be formed from the first 3 letters of the alphabet if no letter can be used more than once?
> Solve for x. 12(x + 5) = x + 122 - 29
> Solve for x. 7x = 51 + 45 - x
> Solve for x. 124 = 73 + 87 - x
> Use formula (2) for the amount to find each of the indicated quantities. A = $410; P = $400; r = 10%; t = ?
> Politics. If 12,457 people voted for a politician in his first election, 15,322 voted for him in his second election, and 9,345 voted for him in the first and second elections, how many people voted for this politician in the first or second election?
> A couple is planning to have 3 children. How many boy–girl combinations are possible? Distinguish between combined outcomes such as (B, B, G), (B, G, B), and (G, B, B). (A) Solve using a tree diagram. (B) Solve using the multiplication principle.
> Refer to the table in Problem 61. (A) How many females are of age 16–19 and earn minimum wage? (B) How many males are of age 16–24 and earn below minimum wage? (C) How many workers are of age 20–24
> A cable company offers its 10,000 customers two special services: high-speed internet and digital phone. If 3,770 customers use high-speed internet, 3,250 use digital phone, and 4,530 do not use either of these services, how many customers use both high-
> A survey of 800 small businesses indicates that 250 own a video conferencing system, 420 own projection equipment, and 180 own a video conferencing system and projection equipment. (A) How many businesses in the survey own either a video conferencing sy
> A manufacturing company in city A wishes to truck its product to 4 different cities: B, C, D, and E. If roads interconnect all 4 cities, how many different route plans can be constructed so that a single truck, starting from A, will visit each city exact
> A corporation plans to fill 2 different positions for vice-president, V1 and V2, from administrative officers in 2 of its manufacturing plants. Plant A has 6 officers and plant B has 8. How many ways can these 2 positions be filled if the V1 position is
> A high school football team with 40 players includes 16 players who played offense last year, 17 who played defense, and 12 who were not on last year’s team. How many players from last year played both offense and defense?
> A class of 30 music students includes 13 who play the piano, 16 who play the guitar, and 5 who play both the piano and the guitar. How many students in the class play neither instrument?
> Refer to the following Venn diagram. Which of the numbers x, y, z, or w must equal 0 if A ∪ B = U?
> If $2,000 is invested at 7% compounded (A) annually (B) quarterly (C) monthly what is the amount after 5 years? How much interest is earned?
> Refer to the following Venn diagram. Which of the numbers x, y, z, or w must equal 0 if A and B are disjoint?
> Explain how three sets, A, B, and C, can be related to each other in order for the following equation to hold true (Venn diagrams may be helpful):
> How many 5-digit ZIP code numbers are possible? How many of these numbers contain no repeated digits?
> A small combination lock has 3 wheels, each labeled with the 10 digits from 0 to 9. How many 3-digit combinations are possible if no digit is repeated? If digits can be repeated? If successive digits must be different?
> Using the English alphabet, how many 5-character case sensitive passwords are possible if each character is a letter or a digit?
> A delicatessen serves meat sandwiches with the following options: 3 kinds of bread, 5 kinds of meat, and lettuce or sprouts. How many different sandwiches are possible, assuming that one item is used out of each category
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample (A) If A and B are disjoint, then n(A ∩ B) = n(A) + n(B). (B) If n(A ∪ B) = n(A) + n(B), then A and B are disjoint.
> Use the given information to complete the following table.
> Use the given information to complete the following table.
> Use the given information to complete the following table.
> Use formula (2) for the amount to find each of the indicated quantities. A = $22,135; P = $19,000; t = 39 weeks; r = ?
> Use the given information to complete the following table.
> Use the given information to determine the number of elements in each of the four disjoint subsets in the following Venn diagram. n(A′) = 70, n(B′) = 170, n(A′ ∩ B′
> Use the given information to determine the number of elements in each of the four disjoint subsets in the following Venn diagram. n(A) = 65, n(B) = 150, n(A ∪ B) = 175, n(U) = 200
> Use the given information to determine the number of elements in each of the four disjoint subsets in the following Venn diagram. n(A) = 40, n(B) = 60, n(A ∩ B) = 20, n(U) = 100
> The 14 colleges of interest to a high school senior include 6 that are expensive (tuition more than $30,000 per year), 7 that are far from home (more than 200 miles away), and 2 that are both expensive and far from home. (A) If the student decides to se
> How many 4-letter code words can be formed from the letters A, B, C, D, E, F, G if no letter is repeated? If letters can be repeated? If adjacent letters must be different?
> A college offers 2 introductory courses in history, 3 in science, 2 in mathematics, 2 in philosophy, and 1 in English. (A) If a freshman takes one course in each area during her first semester, how many course selections are possible? (B) If a part-tim
> Indicate true (T) or false (F). 1 ∊ {10, 11}
> Indicate true (T) or false (F). {3, 2, 1} ⊂ {1, 2, 3, 4}
> Use the given interest rate i per compounding period to find r, the annual rate. 0.47% per month
> Answer yes or no. (If necessary, review Section A.1). If the universal set is the set of integers, is the set of even integers the complement of the set of odd integers?
> Answer yes or no. (If necessary, review Section A.1). Is the set of integers the union of the set of even integers and the set of odd integers?
> Answer yes or no. (If necessary, review Section A.1). Is the set of rational numbers a subset of the set of integers?
> Use the Venn diagram to indicate which of the eight blood types are included in each set. Rh′ ∩ A
> Use the Venn diagram to indicate which of the eight blood types are included in each set. (A ∪ B ∪ Rh)′
> Use the Venn diagram to indicate which of the eight blood types are included in each set. A ∪ B
> Use the Venn diagram to indicate which of the eight blood types are included in each set. A ∩ B
> Voting coalition. The company’s leaders in Problem 89 decide for or against certain measures as follows: The president has 2 votes and each vice-president has 1 vote. Three favorable votes are needed to pass a measure. List all minimal winning coalitions
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Use formula (2) for the amount to find each of the indicated quantities. A = $6,608; r = 24%; t = 3 quarters; P = ?
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Find the indicated number of elements by referring to the following table of enrollments in a finite mathematics class: Let the universal set U be the set of all 120 students in the class, A the set of students from the College of Arts & Sciences, B
> Let A be a set that contains exactly n elements. Find a formula in terms of n for the number of subsets
> Discuss the validity of each statement. Venn diagrams may be helpful. If the statement is true, explain why. If not, give a counter example The empty set is a subset of the empty set.
> Discuss the validity of each statement. Venn diagrams may be helpful. If the statement is true, explain why. If not, give a counter example If A ⊂ B, then B′ ⊂ A′.
> Discuss the validity of each statement. Venn diagrams may be helpful. If the statement is true, explain why. If not, give a counter example If A = ∅, then A ∩ B = ∅.
> Discuss the validity of each statement. Venn diagrams may be helpful. If the statement is true, explain why. If not, give a counter example If A ∩ B = A, then A ⊂ B.
> Use the given interest rate i per compounding period to find r, the annual rate. 3.69% per half-year
> Discuss the validity of each statement. Venn diagrams may be helpful. If the statement is true, explain why. If not, give a counter example If A ⊂ B, then A ∪ B = A.
> Are the given sets disjoint? Let H, T, P, and E denote the sets in Problems 49, 50, 51, and 52, respectively. E and E
> Are the given sets disjoint? Let H, T, P, and E denote the sets in Problems 49, 50, 51, and 52, respectively. E and P
> Draw a Venn diagram for sets A, B, and C and shade the given region. (A ∩ B)′ ∪ C
> Draw a Venn diagram for sets A, B, and C and shade the given region. (A ∪ B)′
> Draw a Venn diagram for sets A, B, and C and shade the given region. A′ ∩ B′ ∩ C
> Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set. {2, 4, 6, 8, 10, … }
> Determine whether the given set is finite or infinite. Consider the set N of positive integers to be the universal set. {n ∈ N| n < 1000}
> For P, Q, and R in Problem 47, find P ∩(Q ∪ R). Data from Problem 47: For P = {1, 2, 3, 4}, Q = {2, 4, 6}, and R = {3, 4, 5,6 }, find P ∪ (Q ∩ R).
> If R = {1, 3, 4} and T = {2, 4, 6}, find (A) {x |x ∊ R and x ∊ T}
> Use formula (2) for the amount to find each of the indicated quantities. P = $3,000; r = 4.5%; t = 30 days; A = ?
> Refer to the Venn diagram below and find the indicated number of elements. n(A ∩ A′)
> Refer to the Venn diagram below and find the indicated number of elements. n(A′ ∩ B′)
> Refer to the Venn diagram below and find the indicated number of elements. n((A ∩ B)′)
> Refer to the Venn diagram below and find the indicated number of elements. n(A ∩ B′)
> Refer to the Venn diagram below and find the indicated number of elements. n(B′)
> Refer to the Venn diagram below and find the indicated number of elements. n(A ∩ B)
> Refer to the Venn diagram below and find the indicated number of elements. n(A)
> For U = {7, 8, 9, 10, 11} and A = {7, 11}, find A′.
> write the resulting set using the listing method. {x | x is a month starting with M}

