Question: Use the table, which shows the years
Use the table, which shows the years of experience of 14 registered nurses and their annual salaries (in thousands of dollars).
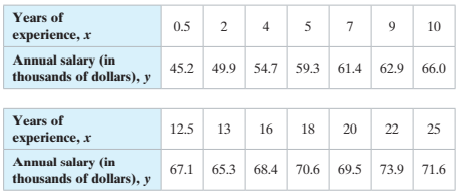
Using the scatter plot of the registered nurse salary data shown below, what type of correlation, if any, do you think the data have? Explain.
Transcribed Image Text:
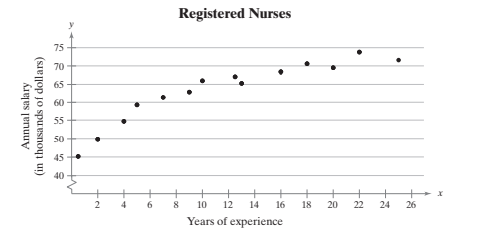
Years of 0.5 4 5 7 9 10 experience, r Annual salary (in thousands of dollars), y 45.2 49.9 54.7 59.3 61.4 62.9 66.0 Years of 12.5 13 16 18 20 22 25 experience, r Annual salary (in thousands of dollars), y 67.1 65.3 68.4 70.6 69.5 73.9 71.6 2. Registered Nurses 75 70 65 60 55 50 45 40 + + + + 10 4 6. 12 14 16 18 20 22 24 26 Years of experience Annual salary (in thousands of dollars)
> Use the figure. Find the standard error of estimate se and interpret the results. Keeping cars longer The median age of vehicles on U.S. roads for eight different years: Median age in years Cars, x Light Trucks, y 10.4 10.5 10.8 11.1 11.3 11.4 11.4
> Use the figure. Find the coefficient of determination r2 and interpret the results. Keeping cars longer The median age of vehicles on U.S. roads for eight different years: Median age in years Cars, x Light Trucks, y 10.4 10.5 10.8 11.1 11.3 11.4 11.
> Use the figure. Find and draw the regression line. Keeping cars longer The median age of vehicles on U.S. roads for eight different years: Median age in years Cars, x Light Trucks, y 10.4 10.5 10.8 11.1 11.3 11.4 11.4 11.5 9.8 10.1 10.5 10.8 11.1 11
> Use the figure. Construct a scatter plot of the data. Show y and x on the graph Keeping cars longer The median age of vehicles on U.S. roads for eight different years: Median age in years Cars, x Light Trucks, y 10.4 10.5 10.8 11.1 11.3 11.4 11.4 11
> Construct the indicated prediction interval and interpret the results. Construct a 99% prediction interval for new-vehicle sales for Honda in Exercise 20 when the number of new vehicles sold by Toyota is 2359 thousand.
> Use the figure. Describe the unexplained variation about a regression line in words and in symbols. (x;. y;). (x;, 7) y = ỹ
> Construct the indicated prediction interval and interpret the results. Construct a 95% prediction interval for new-vehicle sales for General Motors in Exercise 19 when the number of new vehicles sold by Ford is 2628 thousand.
> Construct the indicated prediction interval and interpret the results. Construct a 90% prediction interval for the total assets in federal defined benefit plans in Exercise 18 when the total assets in IRAs is $6200 billion.
> Construct the indicated prediction interval and interpret the results. Construct a 95% prediction interval for the amount of crude oil imported by the United States in Exercise 17 when the amount of crude oil produced by the United States is 8 million ba
> Construct the indicated prediction interval and interpret the results. Construct a 99% prediction interval for number of ballots cast in Exercise 16 when the voting age population is 210 million.
> State H0 and Ha in words and in symbols. Then determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. Explain your reasoning. Sketch a normal sampling distribution and shade the area for the P-value. A report claims that lung c
> a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test, a t-test, or a chi-square test. Explain your reasoning. c. Choose one of the options. Option
> Construct the indicated prediction interval and interpret the results. Construct a 99% prediction interval for the mean annual wage in Exercise 15 when the percentage of employment in STEM occupations is 13% in the industry
> Construct the indicated prediction interval and interpret the results. Construct a 90% prediction interval for the trunk diameter of a tree in Exercise 14 when the height is 80 feet.
> Construct the indicated prediction interval and interpret the results. Construct a 90% prediction interval for total points earned in Exercise 13 when the number of goals allowed by the team is 250.
> Construct the indicated prediction interval and interpret the results. Construct a 95% prediction interval for the median annual earnings of female workers in Exercise 12 when the median annual earnings of male workers is $45,637.
> Construct the indicated prediction interval and interpret the results. Construct a 95% prediction interval for the proceeds from initial public offerings in Exercise 11 when the number of offerings is 450.
> Use the figure. Describe the explained variation about a regression line in words and in symbols. (x;. y;). (x;, 7) y = ỹ
> State H0 and Ha in words and in symbols. Then determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. Explain your reasoning. Sketch a normal sampling distribution and shade the area for the P-value. A golf analyst claims that
> Use the value of the correlation coefficient r to calculate the coefficient of determination r2. What does this tell you about the explained variation of the data about the regression line? about the unexplained variation? r = 0.881
> Use the figure. Describe the total variation about a regression line in words and in symbols. (x;. y;). (x;, 7) y = ỹ
> State H0 and Ha in words and in symbols. Then determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. Explain your reasoning. Sketch a normal sampling distribution and shade the area for the P-value. A manufacturer of grandfath
> Why is it not appropriate to use a regression line to predict y-values for x-values that are not in (or close to) the range of x-values found in the data?
> In order to predict y-values using the equation of a regression line, what must be true about the correlation coefficient of the variables?
> The logarithmic equation is a nonlinear regression equation of the form y = a + b ln x. Use this information and technology. Compare your results in Exercise 46 with the equation of the regression line and its graph. Which equation is a better model for
> The logarithmic equation is a nonlinear regression equation of the form y = a + b ln x. Use this information and technology. Compare your results in Exercise 45 with the equation of the regression line and its graph. Which equation is a better model for
> The logarithmic equation is a nonlinear regression equation of the form y = a + b ln x. Use this information and technology. Find and graph the logarithmic equation for the data in Exercise 26. From Exercise 26: The ages (in years) of 10 infants and the
> The logarithmic equation is a nonlinear regression equation of the form y = a + b ln x. Use this information and technology. Find and graph the logarithmic equation for the data in Exercise 25. From Exercise 25: The shoe sizes and heights (in inches) of
> Use the data shown in the table at the left. Compare your results in Exercise 43 with the equation of the regression line and its graph in Exercise 41. Which equation is a better model for the data? Explain. y 1 695 2 410 3 256 4 110 5 80 75 7 68 8
> Use the data shown in the table at the left. A power equation is a nonlinear regression equation of the form y = axb. Use technology to find and graph the power equation for the original data. Include a scatter plot in your graph. Note that you can also
> Use the data shown in the table at the left. Replace each x-value and y-value in the table with its logarithm. Find the equation of the regression line for the transformed data. Then construct a scatter plot of (log x, log y) and sketch the regression l
> State H0 and Ha in words and in symbols. Then determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. Explain your reasoning. Sketch a normal sampling distribution and shade the area for the P-value. A security expert claims th
> Use the data shown in the table at the left. Find the equation of the regression line for the data. Then construct a scatter plot of (x, y) and sketch the regression line with it. y 1 695 2 410 3 256 4 110 5 80 75 7 68 8 74
> Use the data shown in the table at the left, which shows the number of bacteria present after a certain number of hours. Compare your results in Exercise 39 with the equation of the regression line and its graph in Exercise 37. Which equation is a bette
> For a set of data and a corresponding regression line, describe all values of x that provide meaningful predictions for y.
> Use the data shown in the table at the left, which shows the number of bacteria present after a certain number of hours. An exponential equation is a nonlinear regression equation of the form y = abx. Use technology to find and graph the exponential equ
> Use the data shown in the table at the left, which shows the number of bacteria present after a certain number of hours. Replace each y-value in the table with its logarithm, log y. Find the equation of the regression line for the transformed data. Then
> Use the data shown in the table at the left, which shows the number of bacteria present after a certain number of hours. Find the equation of the regression line for the data. Then construct a scatter plot of (x, y) and sketch the regression line with i
> a. construct a scatter plot of the data, b. identify any possible outliers, and c. determine whether the point is influential. Explain your reasoning. 1 3 6 8 8 12 14 у 4 7 10 9 15 3.
> a. construct a scatter plot of the data, b. identify any possible outliers, and c. determine whether the point is influential. Explain your reasoning. 5 6 9 | 33 28 10 14 17 19 44 32 26 25 23 23 8.
> a. find the equation of the regression line, b. construct a scatter plot of the data and draw the regression line, c. construct a residual plot, and d. determine whether there are any patterns in the residual plot and explain what they suggest about t
> a. find the equation of the regression line, b. construct a scatter plot of the data and draw the regression line, c. construct a residual plot, and d. determine whether there are any patterns in the residual plot and explain what they suggest about t
> Describe type I and type II errors for a hypothesis test of the indicated claim. A cellphone repair shop advertises that the mean cost of repairing a phone screen is less than $75.
> Perform the steps below. a. Find the equation of the regression line for the data, letting Row 1 represent the x-values and Row 2 the y-values. Sketch a scatter plot of the data and draw the regression line. b. Find the equation of the regression line fo
> Perform the steps below. a. Find the equation of the regression line for the data, letting Row 1 represent the x-values and Row 2 the y-values. Sketch a scatter plot of the data and draw the regression line. b. Find the equation of the regression line fo
> Use the table, which shows the years of experience of 14 registered nurses and their annual salaries (in thousands of dollars). A salary analyst claims that the population has a significant correlation for α = 0.01. Test this claim. Ye
> Explain how to predict y-values using the equation of a regression line.
> Use the table, which shows the years of experience of 14 registered nurses and their annual salaries (in thousands of dollars). An analyst used the regression line you found in Exercise 28 to predict the annual salary for a registered nurse with 28 year
> Use the table, which shows the years of experience of 14 registered nurses and their annual salaries (in thousands of dollars). Find an equation of the regression line for the data. Sketch a scatter plot of the data and draw the regression line. Yea
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Describe type I and type II errors for a hypothesis test of the indicated claim. A campus security department publicizes that at most 25% of applicants become campus security officers.
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Two variables have a positive linear correlation. Is the slope of the regression line for the variables positive or negative?
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Find the equation of the regression line for the data. Then construct a scatter plot of the data and draw the regression line. (Each pair of variables has a significant correlation.) Then use the regression equation to predict the value of y for each of
> Describe type I and type II errors for a hypothesis test of the indicated claim. A researcher claims that the percentage of adults in the United States who own a video game system is not 26%.
> What is a residual? Explain when a residual is positive, negative, and zero.
> Determine whether there is a perfect positive linear correlation, a strong positive linear correlation, a perfect negative linear correlation, a strong negative linear correlation, or no linear correlation between the variables.
> In your own words, what does it mean to say “correlation does not imply causation”? List a pair of variables that have correlation but no cause-and-effect relationship.
> What are the null and alternate hypotheses for a two-tailed t-test for the population correlation coefficient ρ? When do you reject the null hypothesis?
> Discuss the difference between r and ρ.
> Describe type I and type II errors for a hypothesis test of the indicated claim. A local chess club claims that the length of time to play a game has a standard deviation of more than 12 minutes.
> Explain how to determine whether a sample correlation coefficient indicates that the population correlation coefficient is significant.
> Give examples of two variables that have perfect positive linear correlation and two variables that have perfect negative linear correlation.
> In Exercise 26, let the time (in seconds) to sprint 10 meters represent the x-values and the maximum weight (in kilograms) for which one repetition of a half squat can be performed represent the y-values. Calculate the correlation coefficient r. What eff
> Perform a hypothesis test using Table 5 in Appendix B to make a conclusion about the correlation coefficient. The table in Exercise 26 shows the maximum weights (in kilograms) for which one repetition of a half squat can be performed and the times (in se
> Perform a hypothesis test using Table 5 in Appendix B to make a conclusion about the correlation coefficient. The table in Exercise 25 shows the maximum weights (in kilograms) for which one repetition of a half squat can be performed and the jump heights
> Perform a hypothesis test using Table 5 in Appendix B to make a conclusion about the correlation coefficient. The weights (in pounds) of eight vehicles and the variabilities of their braking distances (in feet) when stopping on a wet surface are shown in
> Perform a hypothesis test using Table 5 in Appendix B to make a conclusion about the correlation coefficient. The weights (in pounds) of eight vehicles and the variabilities of their braking distances (in feet) when stopping on a dry surface are shown in
> In Exercise 26, add data for an international soccer player who can perform the half squat with a maximum of 210 kilograms and can sprint 10 meters in 2.00 seconds to the data set. Describe how this affects the correlation coefficient r.
> In Exercise 25, remove the data for the international soccer player with a maximum weight of 170 kilograms and a jump height of 64 centimeters from the data set. Describe how this affects the correlation coefficient r.
> In Exercise 24, remove the data for the girl who is 57 inches tall and scored 128 on the IQ test from the data set. Describe how this affects the correlation coefficient r.
> Describe type I and type II errors for a hypothesis test of the indicated claim. An urban planner claims that the noontime mean traffic flow rate on a busy downtown college campus street is 35 cars per minute.
> What does the sample correlation coefficient r measure? Which value indicates a stronger correlation: r = 0.918 or r = -0.932? Explain your reasoning.
> In Exercise 23, add data for a child who is 6 years old and has a vocabulary size of 900 words to the data set. Describe how this affects the correlation coefficient r
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> a. display the data in a scatter plot, b. calculate the sample correlation coefficient r, c. describe the type of correlation, if any, and interpret the correlation in the context of the data, and d. use Table 11 in Appendix B to make a conclusion abo
> Two variables are given that have been shown to have correlation but no cause-and-effect relationship. Describe at least one possible reason for the correlation. Marriage rate in Kentucky and number of deaths caused by falling out of a fishing boat
> Two variables are given that have been shown to have correlation but no cause-and-effect relationship. Describe at least one possible reason for the correlation. Ice cream sales and homicide rates
> Describe type I and type II errors for a hypothesis test of the indicated claim. A used textbook selling website claims that at least 60% of its new customers will return to buy their next textbook.
> Two variables are given that have been shown to have correlation but no cause-and-effect relationship. Describe at least one possible reason for the correlation. Alcohol use and tobacco use
> Describe the range of values for the correlation coefficient.
> Two variables are given that have been shown to have correlation but no cause-and-effect relationship. Describe at least one possible reason for the correlation. Value of home and life span
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> The scatter plots show the results of a survey of 20 randomly selected males ages 24–35. Using age as the explanatory variable, match each graph with the appropriate description. Explain your reasoning. a. Age and body temperature b. A
> Identify the explanatory variable and the response variable. An actuary at an insurance company wants to determine whether the number of hours of safety driving classes can be used to predict the number of driving accidents for each driver.
> Identify the explanatory variable and the response variable. A nutritionist wants to determine whether the amounts of water consumed each day by persons of the same weight and on the same diet can be used to predict individual weight loss.
> Determine whether there is a perfect positive linear correlation, a strong positive linear correlation, a perfect negative linear correlation, a strong negative linear correlation, or no linear correlation between the variables.

