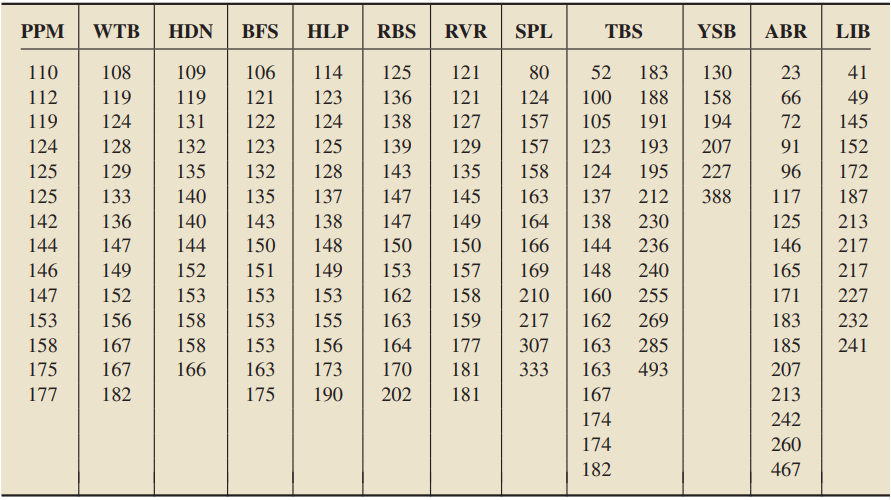
Question: We presented some information on the 12

> Desert Samaritan Hospital in Mesa, Arizona, keeps records of emergency room traffic. Those records reveal that the times between arriving patients have a special type of reverse-J-shaped distribution called an exponential distribution. They also indicate

> We have given population data for a variable. For each exercise, do the following tasks. a. Find the mean, μ, of the variable. b. For each of the possible sample sizes, construct a table and draw a dotplot for the sampling distribution of the sample mean

> For humans, gestation periods are normally distributed with a mean of 266 days and a standard deviation of 16 days. Suppose that you observe the gestation periods for a sample of nine humans. a. Theoretically, what are the mean and standard deviation of

> In an article titled “Great White, Deep Trouble” (National Geographic, Vol. 197(4), pp. 2–29), Peter Benchley—the author of JAWS—discussed various aspects of the Great White Shark (Carcharodon carcharias). Data on the number of pups borne in a lifetime b

> This exercise can be done individually or, better yet, as a class project. a. Use a random-number table or random-number generator to obtain a sample (with replacement) of four digits between 0 and 9. Do so a total of 50 times and compute the mean of eac

> Consider simple random samples of size n without replacement from a population of size N. a. Show that if n ≤ 0.05N, then b. Use part (a) to explain why there is little difference in the values provided by Equations (7.1) and (7.2) when the sample size i

> In Example 7.5, we used the definition of the standard deviation of a variable (Definition 3.12 on page 142) to obtain the standard deviation of the heights of the five starting players on a men’s basketball team and also the standard deviation of x¯ for

> Suppose that a simple random sample is taken without replacement from a finite population of size N. a. Show mathematically that Equations (7.1) and (7.2) are identical for samples of size 1. b. Explain in words why part (a) is true. c. Without doing any

> A statistic is said to be an unbiased estimator of a parameter if the mean of all its possible values equals the parameter; otherwise, it is said to be a biased estimator. An unbiased estimator yields, on average, the correct value of the parameter, wher

> Each year, thousands of high school students bound for college take the Scholastic Assessment Test (SAT). This test measures the verbal and mathematical abilities of prospective college students. Student scores are reported on a scale that ranges from a

> As reported by the U.S. Census Bureau in Educational Attainment in the United States, the percentage of adults in each state who have completed a bachelor’s degree is provided on the WeissStats site. Use the technology of your choice to solve the followi

> According to The Earth: Structure, Composition and Evolution (The Open University, S237), for earthquakes with a magnitude of 7.5 or greater on the Richter scale, the time between successive earthquakes has a mean of 437 days and a standard deviation of

> Alcohol consumption on college and university campuses has gained attention because undergraduate students drink significantly more than young adults who are not students. Researchers I. Balodis et al. studied binge drinking in undergraduates in the arti

> We have given population data for a variable. For each exercise, do the following tasks. a. Find the mean, μ, of the variable. b. For each of the possible sample sizes, construct a table and draw a dotplot for the sampling distribution of the sample mean

> Parkinson’s disease affects internally generated movements such as movements recalled from memory. L-Dopa is a drug that is used in clinical treatment of Parkinson’s disease. In the article, “L-Dopa Induces Under-Damped Visually Guided Motor Responses in

> According to the U.S. Census Bureau publication Manufactured Housing Statistics, the mean price of new mobile homes is $65,100. Assume a standard deviation of $7200. Let x¯ denote the mean price of a sample of new mobile homes. a. For samples of size 50,

> In the article ‘‘Age at Menopause in Puebla, Mexico” (Human Biology, Vol. 75, No. 2, pp. 205 206), authors L. Sievert and S. Hautaniemi compared the age of menopause for different populations. Menopause, the last menstrual period, is a universal phenomen

> The paper ‘‘Are Babies Normal?’’ by T. Clemons and M. Pagano (The American Statistician, Vol. 53, No. 4, pp. 298–302) focused on birth weights of babies. According to the article, the mean birth weight is 3369 grams (7 pounds, 6.5 ounces) with a standard

> Research by R. Pyhala et al. shows that young adults who were born prematurely with very low birth weights (below 1500 grams) have higher blood pressure than those born at term. The study can be found in the article, “Blood Pressure Responses to Physiolo

> Repeat parts (b) and (c) of Exercise 7.41 for samples of size 5. For part (b), use your answer to Exercise 7.15(b). Data from Exercise 7.15: Repeat parts (b)–(e) of Exercise 7.11 for samples of size 5. Data from Exercise 7.11: The winner of the 2012–20

> Repeat parts (b) and (c) of Exercise 7.41 for samples of size 4. For part (b), use your answer to Exercise 7.14(b). Data from Exercise 7.14: Repeat parts (b)–(e) of Exercise 7.11 for samples of size 4. Data from Exercise 7.11: The winner of the 2012–20

> Repeat parts (b) and (c) of Exercise 7.41 for samples of size 3. For part (b), use your answer to Exercise 7.13(b). Data from Exercise 7.13: Repeat parts (b)–(e) of Exercise 7.11 for samples of size 3. Data from Exercise 7.11: The winner of the 2012–20

> Repeat parts (b) and (c) of Exercise 7.41 for samples of size 1. For part (b), use your answer to Exercise 7.12(b). Data from Exercise 7.12: Repeat parts (b)–(e) of Exercise 7.11 for samples of size 1. Data from Exercise 7.11: The winner of the 2012–20

> The winner of the 2012–2013 National Basketball Association (NBA) championship was the Miami Heat. One possible starting lineup for that team is as follows. a. Determine the population mean height, μ, of the five players. b. Consider samples of size 2 wi

> Refer to Exercise 7.10 on page 295. a. Use your answers from Exercise 7.10(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯,

> The number of hospital beds available in community hospitals is decreasing. Through advancement in care and technology, hospitals are getting more efficient. However, the aging and increasingly obese and diabetic population intensifies the need. The Amer

> We have given population data for a variable. For each exercise, do the following tasks. a. Find the mean, μ, of the variable. b. For each of the possible sample sizes, construct a table and draw a dotplot for the sampling distribution of the sample mean

> Refer to Exercise 7.9 on page 295. a. Use your answers from Exercise 7.9(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.8 on page 295. a. Use your answers from Exercise 7.8(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.7 on page 295. a. Use your answers from Exercise 7.7(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.6 on page 295. a. Use your answers from Exercise 7.6(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.5 on page 295. a. Use your answers from Exercise 7.5(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.4 on page 295. a. Use your answers from Exercise 7.4(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> Refer to Exercise 7.3 on page 295. a. Use your answers from Exercise 7.3(b) to determine the mean, μx¯ , of the variable x¯ for each of the possible sample sizes. b. For each of the possible sample sizes, determine the mean, μx¯ , of the variable x¯, usi

> You have seen that the larger the sample size, the smaller the sampling error tends to be in estimating a population mean by a sample mean. This fact is reflected mathematically by the formula for the standard deviation of the sample mean: σx¯ = σ/√n. Fo

> What is another name for the standard deviation of the variable x¯? What is the reason for that name?

> According to the National Health and Nutrition Examination Survey, published by the Centers for Disease Control and Prevention, the average cholesterol level for children between 4 and 19 years of age is 165 mg/dL. A pediatrician who tested the cholester

> Explain why increasing the sample size tends to result in a smaller sampling error when a sample mean is used to estimate a population mean.

> We have given population data for a variable. For each exercise, do the following tasks. a. Find the mean, μ, of the variable. b. For each of the possible sample sizes, construct a table and draw a dotplot for the sampling distribution of the sample mean

> Does the sample size have an effect on the standard deviation of all possible sample means? Explain your answer.

> Does the sample size have an effect on the mean of all possible sample means? Explain your answer.

> Why is obtaining the mean and standard deviation of x¯ a first step in approximating the sampling distribution of the sample mean by a normal distribution?

> Although, in general, you cannot know the sampling distribution of the sample mean exactly, by what distribution can you often approximate it?

> Suppose that a random sample of size 1 is to be taken from a finite population of size N. a. How many possible samples are there? b. Identify the relationship between the possible sample means and the possible observations of the variable under considera

> Suppose that a sample is to be taken without replacement from a finite population of size N. If the sample size is the same as the population size, a. how many possible samples are there? b. what are the possible sample means? c. what is the relationship

> Explain what the dotplots in part (c) of Exercises 7.17–7.22 illustrate about the impact of increasing sample size on sampling error. Data from Exercise 7.17: Each year, Forbes magazine publishes a list of the richest people in the United States. As of

> Repeat parts (b)–(e) of Exercise 7.17 for samples of size 6. What is the relationship between the only possible sample here and the population? Data from Exercise 7.17: Each year, Forbes magazine publishes a list of the richest people in the United Stat

> The Internal Revenue Service (IRS) publishes data on adjusted gross incomes in Statistics of Income, Individual Income Tax Returns. The following relative frequency histogram shows one year’s individual income tax returns for adjusted gross incomes of le

> At the beginning of this chapter, we presented a cross classification of data on eye color and hair color collected as part of a class project by students in an elementary statistics course at the University of Delaware. a. Explain what it would mean for

> n = 10, p = 0.2

> n = 9, p = 0.75

> n = 8, p = 0.5

> n = 6, p = 0.3

> n = 11, p = 0.75, x ≥ 8

> n = 12, p = 0.35, x ≤ 4

> n = 20, p = 0.7, x ≥ 12

> n = 7, p = 0.5, x > 3

> n = 10, p = 0.65, x < 5

> n = 9, p = 0.2, x ≤ 3

> What does it mean when sampling is done without replacement?

> n = 20, p = 0.6, x = 17

> n = 8, p = 0.35, x = 3

> n = 50, p = 0.02, x = 3

> n = 40, p = 0.99, x = 38

> n = 15, p = 0.85, x = 12

> n = 10, p = 0.4, x = 3

> In a town with 400 citizens, 100 randomly selected citizens are asked to identify their religion. The number who identify with a Christian religion is recorded.

> One hundred randomly selected U.S. parents with at least one child under the age of 18 are surveyed and asked if they have ever spanked their child. The number of parents who have spanked their child is recorded.

> A baseball player who reaches base safely 30% of the time is allowed to bat until he reaches base safely for the third time. The number of at-bats required is recorded.

> A basketball player who makes 80% of her free throws is asked to shoot free throws until she misses. The number of free- throw attempts is recorded.

> Define simple random sampling.

> Three cards are selected from a standard 52-card deck with replacement. The number of kings selected is recorded.

> Three cards are selected from a standard 52-card deck without replacement. The number of aces selected is recorded.

> A poll of 1200 registered voters is conducted in which the respondents are asked whether they believe Congress should reform Social Security.

> An experimental drug is administered to 100 randomly selected individuals, with the number of individuals responding favorably recorded.

> A random sample of 30 cars in a used car lot is obtained, and their mileages recorded.

> A random sample of 15 college seniors is obtained, and the individuals selected are asked to state their ages.

> As a rule of thumb, if______ , the probability distribution of a binomial random variable X is approximately bell shaped.

> The expected number of successes in a binomial experiment with n trials and probability of success p is______ .

> The phrase “no more than” is represented by the math symbol ______.

> True or False: In the binomial probability distribution function, nCx represents the number of ways of obtaining x successes in n trials.

> What is a frame?

> What is a random variable?

> A major theme during the 2018 election in both the House and Senate was the popularity of President Trump (a Republican). The scatter diagram below shows the presidential approval rating (percent of registered voters who approve of the job the president

> One question from the Sullivan Statistics Survey I was “How many credit cards do you currently have?” This question was asked only of those individuals who have at least one credit card. Go to www.pearsonhighered.com/sullivanstats to obtain the survey re

> Use the probability distribution from Problem 20 and a DISCRETE command for some statistical software to simulate 100 repetitions of the experiment. Approximate the mean and standard deviation of the random variable X based on the simulation. Repeat the

> After scoring a touchdown in football, the scoring team is entitled to either earn 1 extra point (by kicking the ball through goal posts) or 2 extra points (by advancing the ball past the goal line). Up until the 2016–2017 football season, teams who atte

> Some standardized tests, such as the SAT test, incorporate a penalty for wrong answers. For example, a multiple-choice question with five possible answers will have 1 point awarded for a correct answer and 1/4 point deducted for an incorrect answer. Ques

> Powerball is a multistate lottery. The following probability distribution represents the cash prizes of Powerball with their corresponding probabilities. (a)If the grand prize is $15,000,000, find and interpret the expected cash prize. If a ticket costs

> The following table shows the net winnings from a $1 bet in a video poker game. (a) Compute and interpret the expected net winnings from the player’s point of view. Round your answer to three decimal places (nearest tenth of a penny). (b) Suppose over th

> In the game of roulette, a player can place a $5 bet on the number 17 and have a 1/38 probability of winning. If the metal ball lands on 17, the player wins $175. Otherwise, the casino takes the player’s $5. What is the expected value of the game to the

> An investment counselor calls with a hot stock tip. He believes that if the economy remains strong, the investment will result in a profit of $50,000. If the economy grows at a moderate pace, the investment will result in a profit of $10,000. However, if

> Open the data set 1_3_17 from www.pearsonhighered.com/sullivanstats. The data set represents a list of every high school in the city of Chicago. Suppose you wish to conduct a survey of all the students enrolled for a simple random sample of 8 high school

> Blackjack is a popular casino game in which a player is dealt two cards where the value of the card corresponds to the number on the card, face cards are worth ten, and aces are worth either one or eleven. The object is to get as close to 21 as possible

> To the nearest dollar, what is the standard deviation of the value of the life insurance policy from Problem 26? Why is the value so high?

> To the nearest dollar, what is the standard deviation of the value of the life insurance policy from Problem 25? Why is the value so high?

> A life insurance company sells a $250,000 1-year term life insurance policy to a 20-year-old male for $350. According to the National Vital Statistics Report, 58(21), the probability that the male survives the year is 0.998734. Compute and interpret the

> A life insurance company sells a $250,000 1-year term life insurance policy to a 20-year-old female for $200. According to the National Vital Statistics Report, 58(21), the probability that the female survives the year is 0.999544. Compute and interpret

> The graph of the discrete probability distribution represents the number of rooms in rented housing units in 2017. Source: U.S. Department of Commerce. (a) What is the probability that a randomly selected rental unit has five rooms? (b) What is the proba

> The graph of the discrete probability distribution below represents the number of live births by a mother 50–54 years old who had a live birth in 2017. Source: National Vital Statistics Report. (a) What is the probability that a randomly selected 50- to