Question: You are designing a two-string instrument
You are designing a two-string instrument with metal strings 35.0 cm long, as shown in Fig. P15.54. Both strings are under the same tension. String S1 has a mass of 8.00 g and produces the note middle C (frequency 262 Hz) in its fundamental mode.
(a) What should be the tension in the string?
(b) What should be the mass of string S2 so that it will produce A-sharp (frequency 466 Hz) as its fundamental?
(c) To extend the range of your instrument, you include a fret located just under the strings but not normally touching them. How far from the upper end should you put this fret so that when you press S1 tightly against it, this string will produce C-sharp (frequency 277 Hz) in its fundamental? That is, what is x in the figure?
(d) If you press S2 against the fret, what frequency of sound will it produce in its fundamental?
Fig. P15.54:
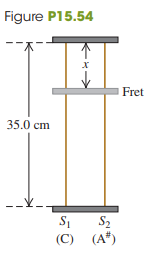
Transcribed Image Text:
Figure P15.54 Fret 35.0 cm S2 (C) (A*)
> Consider a spacecraft in an elliptical orbit around the earth. At the low point, or perigee, of its orbit, it is 400 km above the earth’s surface; at the high point, or apogee, it is 4000 km above the earth’s surface. (a) What is the period of the spacec
> The planet Uranus has a radius of 25,360 km and a surface acceleration due to gravity of 9.0 m>s2 at its poles. Its moon Miranda (discovered by Kuiper in 1948) is in a circular orbit about Uranus at an altitude of 104,000 km above the planet’s surface. M
> At what point in the motion of a simple pendulum is the string tension greatest? Least? In each case give the reasoning behind your answer.
> Comets travel around the sun in elliptical orbits with large eccentricities. If a comet has speed 2.0 × 104 m/s when at a distance of 2.5 × 1011 m from the center of the sun, what is its speed when at a distance of 5.0 × 1010 m?
> Two stars, with masses M1 and M2, are in circular orbits around their center of mass. The star with mass M1 has an orbit of radius R1; the star with mass M2 has an orbit of radius R2. (a) Show that the ratio of the orbital radii of the two stars equals t
> Two identical stars with mass M orbit around their center of mass. Each orbit is circular and has radius R, so that the two stars are always on opposite sides of the circle. (a) Find the gravitational force of one star on the other. (b) Find the orbital
> The preceding problems in this chapter have assumed that the springs had negligible mass. But of course no spring is completely massless. To find the effect of the spring’s mass, consider a spring with mass M, equilibrium length L0, and spring constant k
> Two springs with the same unstretched length but different force constants k1 and k2 are attached to a block with mass m on a level, frictionless surface. Calculate the effective force constant keff in each of the three cases (a), (b), and (c) depicted i
> On July 4, 2005, the NASA spacecraft Deep Impact fired a projectile onto the surface of Comet Tempel 1. This comet is about 9.0 km across. Observations of surface debris released by the impact showed that dust with a speed as low as 1.0 m/s was able to e
> An unmanned spacecraft is in a circular orbit around the moon, observing the lunar surface from an altitude of 50.0 km (see Appendix F). To the dismay of scientists on earth, an electrical fault causes an on-board thruster to fire, decreasing the speed o
> The 0.100-kg sphere in Fig. P13.58 is released from rest at the position shown in the sketch, with its center 0.400 m from the center of the 5.00-kg mass. Assume that the only forces on the 0.100-kg sphere are the gravitational forces exerted by the othe
> You are exploring a distant planet. When your spaceship is in a circular orbit at a distance of 630 km above the planet’s surface, the ship’s orbital speed is 4900 m/s. By observing the planet, you determine its radius to be 4.48 × 106 m. You then land o
> Your starship, the Aimless Wanderer, lands on the mysterious planet Mongo. As chief scientist-engineer, you make the following measurements: A 2.50-kg stone thrown upward from the ground at 12.0 m/s returns to the ground in 4.80 s; the circumference of M
> Can a standing wave be produced on a string by superposing two waves traveling in opposite directions with the same frequency but different amplitudes? Why or why not? Can a standing wave be produced by superposing two waves traveling in opposite directi
> An astronaut, whose mission is to go where no one has gone before, lands on a spherical planet in a distant galaxy. As she stands on the surface of the planet, she releases a small rock from rest and finds that it takes the rock 0.480 s to fall 1.90 m. I
> (a) Suppose you are at the earth’s equator and observe a satellite passing directly overhead and moving from west to east in the sky. Exactly 12.0 hours later, you again observe this satellite to be directly overhead. How far above the earth’s surface is
> Planet X rotates in the same manner as the earth, around an axis through its north and south poles, and is perfectly spherical. An astronaut who weighs 943.0 N on the earth weighs 915.0 N at the north pole of Planet X and only 850.0 N at its equator. The
> A landing craft with mass 12,500 kg is in a circular orbit 5.75 × 105 m above the surface of a planet. The period of the orbit is 5800 s. The astronauts in the lander measure the diameter of the planet to be 9.60 × 106 m. The lander sets down at the nort
> What is the escape speed from a 300-km-diameter asteroid with a density of 2500 kg/m3?
> Mass M is distributed uniformly over a disk of radius a. Find the gravitational force (magnitude and direction) between this disk-shaped mass and a particle with mass m located a distance x above the center of the disk (Fig. P13.81). Does your result red
> An astronaut inside a spacecraft, which protects her from harmful radiation, is orbiting a black hole at a distance of 120 km from its center. The black hole is 5.00 times the mass of the sun and has a Schwarzschild radius of 15.0 km. The astronaut is po
> The most efficient way to send a spacecraft from the earth to another planet is to use a Hohmann transfer orbit (Fig. P13.79). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose pe
> For a planet in our solar system, assume that the axis of orbit is at the sun and is circular. Then the angular momentum about that axis due to the planet’s orbital motion is L = MvR. (a) Derive an expression for L in terms of the planet’s mass M, orbita
> A deep-sea diver is suspended beneath the surface of Loch Ness by a 100-m-long cable that is attached to a boat on the surface (Fig. P15.77). The diver and his suit have a total mass of 120 kg and a volume of 0.0800 m3. The cable has a diameter of 2.00 c
> A planet makes a circular orbit with period T around a star. If the planet were to orbit at the same distance around this star, but the planet had three times as much mass, what would the new period (in terms of T) be: (a) 3T, (b) T√3, (c) T, (d) T/√3,
> You are measuring the frequency dependence of the average power Pav transmitted by traveling waves on a wire. In your experiment you use a wire with linear mass density 3.5 g/m. For a transverse wave on the wire with amplitude 4.0 mm, you measure Pav (in
> In your physics lab, an oscillator is attached to one end of a horizontal string. The other end of the string passes over a frictionless pulley. You suspend a mass M from the free end of the string, producing tension Mg in the string. The oscillator prod
> Scale length is the length of the part of a guitar string that is free to vibrate. A standard value of scale length for an acoustic guitar is 25.5 in. The frequency of the fundamental standing wave on a string is determined by the stringâ€
> A musician tunes the C-string of her instrument to a fundamental frequency of 65.4 Hz. The vibrating portion of the string is 0.600 m long and has a mass of 14.4 g. (a) With what tension must the musician stretch it? (b) What percent increase in tension
> A string or rope will break apart if it is placed under too much tensile stress [see Eq. (11.8)]. Thicker ropes can withstand more tension without breaking because the thicker the rope, the greater the cross-sectional area and the smaller the stress. One
> A large rock that weighs 164.0 N is suspended from the lower end of a thin wire that is 3.00 m long. The density of the rock is 3200 kg/m3. The mass of the wire is small enough that its effect on the tension in the wire can be ignored. The upper end of t
> A string with both ends held fixed is vibrating in its third harmonic. The waves have a speed of 192 m/s and a frequency of 240 Hz. The amplitude of the standing wave at an antinode is 0.400 cm. (a) Calculate the amplitude at points on the string a dista
> A uniform cylindrical steel wire, 55.0 cm long and 1.14 mm in diameter, is fixed at both ends. To what tension must it be adjusted so that, when vibrating in its first overtone, it produces the note D-sharp of frequency 311 Hz? Assume that it stretches a
> A guitar string is vibrating in its fundamental mode, with nodes at each end. The length of the segment of the string that is free to vibrate is 0.386 m. The maximum transverse acceleration of a point at the middle of the segment is 8.40 × 103 m/s2 and t
> A thin string 2.50 m in length is stretched with a tension of 90.0 N between two supports. When the string vibrates in its first overtone, a point at an antinode of the standing wave on the string has an amplitude of 3.50 cm and a maximum transverse spee
> If a projectile is fired straight up from the earth’s surface, what would happen if the total mechanical energy (kinetic plus potential) is (a) less than zero, and (b) greater than zero? In each case, ignore air resistance and the gravitational effects o
> A strong string of mass 3.00 g and length 2.20 m is tied to supports at each end and is vibrating in its fundamental mode. The maximum transverse speed of a point at the middle of the string is 9.00 m/s. The tension in the string is 330 N. (a) What is th
> Clothesline Nodes. Cousin Throckmorton is once again playing with the clothesline in Example 15.2 (Section 15.3). One end of the clothesline is attached to a vertical post. Throcky holds the other end loosely in his hand, so the speed of waves on the cl
> A vibrating string 50.0 cm long is under a tension of 1.00 N. The results from five successive stroboscopic pictures are shown in Fig. P15.64. The strobe rate is set at 5000 flashes per minute, and observations reveal that the maximum displacement occurr
> A sinusoidal transverse wave travels on a string. The string has length 8.00 m and mass 6.00 g. The wave speed is 30.0 m>s, and the wavelength is 0.200 m. (a) If the wave is to have an average power of 50.0 W, what must be the amplitude of the wave? (b)
> A vertical, 1.20-m length of 18-gauge (diameter of 1.024 mm) copper wire has a 100.0-N ball hanging from it. (a) What is the wavelength of the third harmonic for this wire? (b) A 500.0-N ball now replaces the original ball. What is the change in the wave
> A horizontal wire is tied to supports at each end and vibrates in its second-overtone standing wave. The tension in the wire is 5.00 N, and the node-to-node distance in the standing wave is 6.28 cm. (a) What is the length of the wire? (b) A point at an a
> A continuous succession of sinusoidal wave pulses are produced at one end of a very long string and travel along the length of the string. The wave has frequency 70.0 Hz, amplitude 5.00 mm, and wavelength 0.600 m. (a) How long does it take the wave to tr
> A 1.80-m-long uniform bar that weighs 638 N is suspended in a horizontal position by two vertical wires that are attached to the ceiling. One wire is aluminum and the other is copper. The aluminum wire is attached to the left-hand end of the bar, and the
> A 0.800-m-long string with linear mass density m = 7.50 g/m is stretched between two supports. The string has tension F and a standing-wave pattern (not the fundamental) of frequency 624 Hz. With the same tension, the next higher standing-wave frequency
> For a string stretched between two supports, two successive standing-wave frequencies are 525 Hz and 630 Hz. There are other standing-wave frequencies lower than 525 Hz and higher than 630 Hz. If the speed of transverse waves on the string is 384 m/s, wh
> Does the escape speed for an object at the earth’s surface depend on the direction in which it is launched? Explain. Does your answer depend on whether or not you include the effects of air resistance?
> You are exploring a newly discovered planet. The radius of the planet is 7.20 × 107 m. You suspend a lead weight from the lower end of a light string that is 4.00 m long and has mass 0.0280 kg. You measure that it takes 0.0685 s for a transverse pulse to
> A 5.00-m, 0.732-kg wire is used to support two uniform 235-N posts of equal length (Fig. P15.55). Assume that the wire is essentially horizontal and that the speed of sound is 344 m/s. A strong wind is blowing, causing the wire to vibrate in its 5th over
> You must determine the length of a long, thin wire that is suspended from the ceiling in the atrium of a tall building. A 2.00-cm-long piece of the wire is left over from its installation. Using an analytical balance, you determine that the mass of the s
> An ant with mass m is standing peacefully on top of a horizontal, stretched rope. The rope has mass per unit length m and is under tension F. Without warning, Cousin Throckmorton starts a sinusoidal transverse wave of wavelength l propagating along the r
> Three pieces of string, each of length L, are joined together end to end, to make a combined string of length 3L. The first piece of string has mass per unit length m1, the second piece has mass per unit length
> A 1750-N irregular beam is hanging horizontally by its ends from the ceiling by two vertical wires (A and B), each 1.25 m long and weighing 0.290 N. The center of gravity of this beam is one-third of the way along the beam from the end where wire A is at
> A transverse sine wave with an amplitude of 2.50 mm and a wavelength of 1.80 m travels from left to right along a long, horizontal, stretched string with a speed of 36.0 m/s. Take the origin at the left end of the undisturbed string. At time t = 0 the le
> A transverse wave on a rope is given by (a) Find the amplitude, period, frequency, wavelength, and speed of propagation. (b) Sketch the shape of the rope at these values of t: 0, 0.0005 s, 0.0010 s. (c) Is the wave traveling in the +x- or -x-direction?
> CP An experiment is performed in deep space with two uniform spheres, one with mass 50.0 kg and the other with mass 100.0 kg. They have equal radii, r = 0.20 m. The spheres are released from rest with their centers 40.0 m apart. They accelerate toward ea
> A planet is moving at constant speed in a circular orbit around a star. In one complete orbit, what is the net amount of work done on the planet by the star’s gravitational force: positive, negative, or zero? What if the planet’s orbit is an ellipse, so
> On December 25, 2004, the Huygens probe separated from the Cassini spacecraft orbiting Saturn and began a 22-day journey to Saturn’s giant moon Titan, on whose surface it landed. Besides the data in Appendix F, it is useful to know that Titan is 1.22 × 1
> A uniform sphere with mass 50.0 kg is held with its center at the origin, and a second uniform sphere with mass 80.0 kg is held with its center at the point x = 0, y = 3.00 m. (a) What are the magnitude and direction of the net gravitational force due to
> There is strong evidence that Europa, a satellite of Jupiter, has a liquid ocean beneath its icy surface. Many scientists think we should land a vehicle there to search for life. Before launching it, we would want to test such a lander under the gravity
> Three uniform spheres are fixed at the positions shown in Fig. P13.43. (a) What are the magnitude and direction of the force on a 0.0150-kg particle placed at P? (b) If the spheres are in deep outer space and a 0.0150-kg particle is released from rest 30
> Four identical masses of 8.00 kg each are placed at the corners of a square whose side length is 2.00 m. What is the net gravitational force (magnitude and direction) on one of the masses, due to the other three?
> Neutron stars, such as the one at the center of the Crab Nebula, have about the same mass as our sun but have a much smaller diameter. If you weigh 675 N on the earth, what would you weigh at the surface of a neutron star that has the same mass as our su
> A piano tuner stretches a steel piano wire with a tension of 800 N. The steel wire is 0.400 m long and has a mass of 3.00 g. (a) What is the frequency of its fundamental mode of vibration? (b) What is the number of the highest harmonic that could be hear
> Is it possible to have a longitudinal wave on a stretched string? Why or why not? Is it possible to have a transverse wave on a steel rod? Again, why or why not? If your answer is yes in either case, explain how you would create such a wave.
> Since the moon is constantly attracted toward the earth by the gravitational interaction, why doesn’t it crash into the earth?
> A wire with mass 40.0 g is stretched so that its ends are tied down at points 80.0 cm apart. The wire vibrates in its fundamental mode with frequency 60.0 Hz and with an amplitude at the antinodes of 0.300 cm. (a) What is the speed of propagation of tran
> When will you attract the sun more: today at noon, or tonight at midnight? Explain.
> Example 13.2 (Section 13.1) shows that the acceleration of each sphere caused by the gravitational force is inversely proportional to the mass of that sphere. So why does the force of gravity give all masses the same acceleration when they are dropped ne
> Is a pound of butter on the earth the same amount as a pound of butter on Mars? What about a kilogram of butter? Explain.
> Two waves travel on the same string. Is it possible for them to have (a) different frequencies; (b) different wavelengths; (c) different speeds; (d) different amplitudes; (e) the same frequency but different wavelengths? Explain your reasoning.
> Two waves travel on the same string. Is it possible for them to have (a) different frequencies; (b) different wavelengths; (c) different speeds; (d) different amplitudes; (e) the same frequency but different wavelengths? Explain your reasoning.
> If a uniform spring is cut in half, what is the force constant of each half? Justify your answer. How would the frequency of SHM using a half-spring differ from the frequency using the same mass and the entire spring?
> In designing structures in an earthquake-prone region, how should the natural frequencies of oscillation of a structure relate to typical earthquake frequencies? Why? Should the structure have a large or small amount of damping?
> Could a standard of time be based on the period of a certain standard pendulum? What advantages and disadvantages would such a standard have compared to the actual present-day standard discussed in Section 1.3?
> Why do short dogs (like Chihuahuas) walk with quicker strides than do tall dogs (like Great Danes)?
> If a pendulum clock is taken to a mountaintop, does it gain or lose time, assuming it is correct at a lower elevation? Explain.
> A 1.50-m-long rope is stretched between two supports with a tension that makes the speed of transverse waves 62.0 m/s. What are the wavelength and frequency of (a) the fundamental; (b) the second overtone; (c) the fourth harmonic?
> What should you do to the length of the string of a simple pendulum to (a) double its frequency; (b) double its period; (c) double its angular frequency?
> The sun pulls on the moon with a force that is more than twice the magnitude of the force with which the earth attracts the moon. Why, then, doesn’t the sun take the moon away from the earth?
> As part of their training before going into orbit, astronauts ride in an airliner that is flown along the same parabolic trajectory as a freely falling projectile. Explain why this gives the same experience of apparent weightlessness as being in orbit.
> In the elliptical orbit of Comet Halley shown in Fig. 13.21a, the sun’s gravity is responsible for making the comet fall inward from aphelion to perihelion. But what is responsible for making the comet move from perihelion back outward
> A communications firm wants to place a satellite in orbit so that it is always directly above the earth’s 45th parallel (latitude 45° north). This means that the plane of the orbit will not pass through the center of the earth. Is such an orbit possible?
> Discuss whether this statement is correct: “In the absence of air resistance, the trajectory of a projectile thrown near the earth’s surface is an ellipse, not a parabola.”
> What is the purpose of the frets on a guitar? In terms of the frequency of the vibration of the strings, explain their use.
> Violins are short instruments, while cellos and basses are long. In terms of the frequency of the waves they produce, explain why this is so.
> As we discussed in Section 15.1, water waves are a combination of longitudinal and transverse waves. Defend the following statement: “When water waves hit a vertical wall, the wall is a node of the longitudinal displacement but an antinode of the transve
> By touching a string lightly at its center while bowing, a violinist can produce a note exactly one octave above the note to which the string is tuned—that is, a note with exactly twice the frequency. Why is this possible?
> Standing waves on a wire are described by Eq. (15.28), with ASW = 2.50 mm,
> A sinusoidal wave can be described by a cosine function, which is negative just as often as positive. So why isn’t the average power delivered by this wave zero?
> At what point in an elliptical orbit is the acceleration maximum? At what point is it minimum? Justify your answers.
> If you stretch a rubber band and pluck it, you hear a (somewhat) musical tone. How does the frequency of this tone change as you stretch the rubber band further? (Try it!) Does this agree with Eq. (15.35) for a string fixed at both ends? Explain.
> The earth is closer to the sun in November than in May. In which of these months does it move faster in its orbit? Explain why.
> Energy can be transferred along a string by wave motion. However, in a standing wave on a string, no energy can ever be transferred past a node. Why not?
> In a transverse wave on a string, the motion of the string is perpendicular to the length of the string. How, then, is it possible for energy to move along the length of the string?
> A long rope with mass m is suspended from the ceiling and hangs vertically. A wave pulse is produced at the lower end of the rope, and the pulse travels up the rope. Does the speed of the wave pulse change as it moves up the rope, and if so, does it incr
> Two strings of different mass per unit length m1 and m2 are tied together and stretched with a tension F. A wave travels along the string and passes the discontinuity in m. Which of the following wave properties will be the same on both sides of the disc
> Which takes more fuel: a voyage from the earth to the moon or from the moon to the earth? Explain.
> The four strings on a violin have different thicknesses, but are all under approximately the same tension. Do waves travel faster on the thick strings or the thin strings? Why? How does the fundamental vibration frequency compare for the thick versus the
> Does a tuning fork or similar tuning instrument undergo SHM? Why is this a crucial question for musicians?

