Question: A baseball diamond is a square with
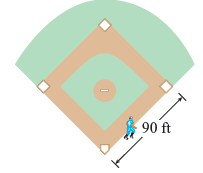
A baseball diamond is a square with side 90 ft. A batter hits the ball and runs toward first base with a speed of 24 ft/s.
(a) At what rate is his distance from second base decreasing when he is halfway to first base?
(b) At what rate is his distance from third base increasing at the same moment?
Transcribed Image Text:
90 ft
> A ladder 10 ft long rests against a vertical wall. Let be the angle between the top of the ladder and the wall and let x be the distance from the bottom of the ladder to the wall. If the bottom of the ladder slides away from the wall, how fast does x c
> For any vectors u and v in V3, |u × v | = |u ||v |.
> For any vectors u and v in V3, |u ∙ v | = |u ||v |.
> For any vectors u and v in V3, |u + v | = |u | + |v |.
> Find an equation of the tangent line to the given curve at the specified point. Y = x2 -1 / x2 + x + 1
> If u and v are in V3, then |u ∙ v | < |u | |v |.
> If u ∙ v = 0 and u × v = 0, then u = 0 or v = 0.
> If u × v = 0, then u = 0 or v = 0.
> An oil storage tank ruptures at time t = 0 and oil leaks from the tank at a rate of r(t) = 100e-0.01t liters per minute. How much oil leaks out during the first hour?
> If u ∙ v = 0, then u = 0 or v = 0.
> In R3 the graph of y = x2 is a paraboloid.
> The set of points {(x, y, z) | x2 + y2 = 1} is a circle.
> A linear equation Ax + By + Cz + D = 0 represents a line in space.
> The vector 3, −1, 2 is parallel to the plane 6x - 2y + 4z = 1
> For any vectors u and v in V3, (u + v) × v = u × v.
> For any vectors u and v in V3, (u × v) ∙ u = 0.
> An elastic band is hung on a hook and a mass is hung on the lower end of the band. When the mass is pulled downward and then released, it vibrates vertically. The equation of motion is s = 2 cos t + 3 sin t, t ≥ 0, where s is measured in centimeters and
> For any vectors u, v, and w in V3, u × (v × w) = (u × v) × w
> For any vectors u, v, and w in V3, u ∙ (v × w) = (u × v) ∙ w
> For any vectors u, v, and w in V3, (u + v) × w = u × w + v × w
> For any vectors u and v in V3 and any scalar k, K (u × v) = (ku) × v
> For any vectors u and v in V3 and any scalar k, K (u ∙ v) = (ku) ∙ v
> For any vectors u and v in V3, u × v = v × u.
> For any vectors u and v in V3, u ∙ v = v ∙ u.
> (a) Draw the line y = 2t + 1 and use geometry to find the area under this line, above the t-axis, and between the vertical lines t = 1 and t = 3. / //
> A mass on a spring vibrates horizontally on a smooth level surface (see the figure). Its equation of motion is x(t) = 8 sin t, where t is in seconds and x in centimeters. (a) Find the velocity and acceleration at time t. (b) Find the position, velocity,
> Which of the following areas are equal? Why? y. yA y= 2xe" y = evt y = esin x sin 2x 2
> Two sides of a triangle have lengths 12 m and 15 m. The angle between them is increasing at a rate of 2º /min. How fast is the length of the third side increasing when the angle between the sides of fixed length is 60°?
> Brain weight B as a function of body weight W in fish has been modeled by the power function B = 0.007W2/3, where B and W are measured in grams. A model for body weight as a function of body length L (measured in centimeters) is W = 0.12L2.53. If, over 1
> If g(x) + x sin g(x) = x2, find g’(0).
> When air expands adiabatically (without gaining or losing heat), its pressure P and volume V are related by the equation PV1.4 = C, where C is a constant. Suppose that at a certain instant the volume is 400 cm3 and the pressure is 80 kPa and is decreasin
> Boyle’s Law states that when a sample of gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation PV = C, where C is a constant. Suppose that at a certain instant the volume is 600 cm3, the pressure is 150 kPa, and th
> A faucet is filling a hemispherical basin of diameter 60 cm with water at a rate of 2 L/min. Find the rate at which the water is rising in the basin when it is half full. [Use the following facts: 1 L is 1000 cm3. The volume of the portion of a sphere wi
> If the minute hand of a clock has length r (in centimeters), find the rate at which it sweeps out area as a function of r.
> According to the model we used to solve Example 2, what happens as the top of the ladder approaches the ground? Is the model appropriate for small values of y? Data from Example 2: A ladder 10 ft long rests against a vertical wall. If the bottom of the
> The top of a ladder slides down a vertical wall at a rate of 0.15 m/s. At the moment when the bottom of the ladder is 3 m from the wall, it slides away from the wall at a rate of 0.2 m/s. How long is the ladder?
> How fast is the angle between the ladder and the ground changing in Example 2 when the bottom of the ladder is 6 ft from the wall? Data from Example 2: A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the w
> The sides of an equilateral triangle are increasing at a rate of 10 cm/min. At what rate is the area of the triangle increasing when the sides are 30 cm long?
> A kite 100 ft above the ground moves horizontally at a speed of 8 ft/s. At what rate is the angle between the string and the horizontal decreasing when 200 ft of string has been let out?
> Gravel is being dumped from a conveyor belt at a rate of 30 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 10
> If f (x) + x2 [f (x)]3 = 10 and f (1) = 2, find f ‘(1).
> A swimming pool is 20 ft wide, 40 ft long, 3 ft deep at the shallow end, and 9 ft deep at its deepest point. A crosssection is shown in the figure. If the pool is being filled at a rate of 0.8 ft3/min, how fast is the water level rising when the depth at
> A water trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of 0.2 m3/min, how fast is the wat
> A trough is 10 ft long and its ends have the shape of isosceles triangles that are 3 ft across at the top and have a height of 1 ft. If the trough is being filled with water at a rate of 12 ft3/min, how fast is the water level rising when the water is 6
> Water is leaking out of an inverted conical tank at a rate of 10,000 cm3/min at the same time that water is being pumped into the tank at a constant rate. The tank has height 6 m and the diameter at the top is 4 m. If the water level is rising at a rate
> A particle moves along the curve y = 2 sins(πx/2). As the particle passes through the point (1/3 , 1), its x-coordinate increases at a rate of 10 cm/s. How fast is the distance from the particle to the origin changing at this instant?
> At noon, ship A is 100 km west of ship B. Ship A is sailing south at 35 km/h and ship B is sailing north at 25 km/h. How fast is the distance between the ships changing at 4:00 pm?
> A boat is pulled into a dock by a rope attached to the bow of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. If the rope is pulled in at a rate of 1 m/s, how fast is the boat approaching the dock when it is
> The altitude of a triangle is increasing at a rate of 1 cm/min while the area of the triangle is increasing at a rate of 2 cm2/min. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 100 cm2?
> A man starts walking north at 4 ft/s from a point P. Five minutes later a woman starts walking south at 5 ft/s from a point 500 ft due east of P. At what rate are the people moving apart 15 min after the woman starts walking?
> Find dy/dx by implicit differentiation. Tan(x – y) = y / 1 + x2
> Find f ’ (x) and f ’’ (x). f (x) = (x3 + 1) ex
> A spotlight on the ground shines on a wall 12 m away. If a man 2 m tall walks from the spotlight toward the building at a speed of 1.6 m/s, how fast is the length of his shadow on the building decreasing when he is 4 m from the building?
> Two cars start moving from the same point. One travels south at 60 mi/h and the other travels west at 25 mi/h. At what rate is the distance between the cars increasing two hours later?
> (a) What quantities are given in the problem? (b) What is the unknown? (c) Draw a picture of the situation for any time t. (d) Write an equation that relates the quantities. (e) Finish solving the problem. At noon, ship A is 150 km west of ship B. Ship A
> (a) What quantities are given in the problem? (b) What is the unknown? (c) Draw a picture of the situation for any time t. (d) Write an equation that relates the quantities. (e) Finish solving the problem. A street light is mounted at the top of a 15-ft-
> For what values of x does the graph of f have a horizontal tangent? f (x) = ex cos x
> Use a graph to give a rough estimate of the area of the region that lies under the given curve. Then find the exact area. y = 2 sin x - sin 2x, 0 ≤ x ≤ π
> The graph of the acceleration a(t) of a car measured in ft/s2 is shown. Use the Midpoint Rule to estimate the increase in the velocity of the car during the six-second time interval. a 12 4 4 6 t(seconds) 2. 00
> Suppose f (π/3) = 4 and f ‘(π/3) = 22, and let g(x)d = f (x) sin x and h(x) = (cos x)/f (x). Find (a) g’(π/3) (b) h’(π/3)
> Water flows into and out of a storage tank. A graph of the rate of change r(t) of the volume of water in the tank, in liters per day, is shown. If the amount of water in the tank at time t = 0 is 25,000 L, use the Midpoint Rule to estimate the amount of
> (a) Use the Quotient Rule to differentiate the function f (x) = tan x – 1 / sec x (b) Simplify the expression for f (x) by writing it in terms of sin x and cos x, and then find f ‘(x). (c) Show that your answers to parts (a) and (b) are equivalent.
> If f (t) = sec t, find f’’ (π/4).
> Suppose that a volcano is erupting and readings of the rate r(t) at which solid materials are spewed into the atmosphere are given in the table. The time t is measured in seconds and the units for r(t) are tonnes (metric tons) per second. (a) Give uppe
> If H( θ) = θ sin θ , find H’( θ) and H’’(θ ).
> Find dy/dx by implicit differentiation. ex/y = x - y
> The velocity of a car was read from its speedometer at 10-second intervals and recorded in the table. Use the Midpoint Rule to estimate the distance traveled by the car. 1 (s) v (mi/h) t (s) v (mi/h) 60 56 10 38 70 53 20 52 80 50 30 58 90 47 40 55 1
> (a) If f (x) = ex cos x, find f ‘(x) an) f ‘’(x). (b) Check to see that your answers to part (a) are reasonable by graphing f , f ‘, and f ‘’.
> Water flows from the bottom of a storage tank at a rate of r(t) = 200 - 4t liters per minute, where 0 ≤ t ≤ 50. Find the amount of water that flows from the tank during the first 10 minutes.
> (a) If f (x) = sec x - x, find f ‘(x). (b) Check to see that your answer to part (a) is reasonable by graphing both f and f‘ for |x | , π/2.
> Find f ’ (x) and f ’’ (x). f(x) = x / x2 - 1
> The acceleration function (in m/s2 ) and the initial velocity are given for a particle moving along a line. Find (a) the velocity at time t and (b) the distance traveled during the given time interval. a(t) = 2t + 3, v(0) = 24, 0 ≤ t ≤ 3
> On May 7, 1992, the space shuttle Endeavour was launched on mission STS-49, the purpose of which was to install a new perigee kick motor in an Intelsat communications satellite. The table gives the velocity data for the shuttle between liftoff and the je
> Shown is the power consumption in the province of Ontario, Canada, for December 9, 2004 (P is measured in megawatts; t is measured in hours starting at midnight). Using the fact that power is the rate of change of energy, estimate the energy used on that
> Shown is the graph of traffic on an Internet service provider’s T1 data line from midnight to 8:00 am. D is the data throughput, measured in megabits per second. Use the Midpoint Rule to estimate the total amount of data transmitted dur
> A bacteria population is 4000 at time t = 0 and its rate of growth is 1000 . 2t bacteria per hour after t hours. What is the population after one hour?
> (a) Fin) an equation of the tangent line to the curve y = 3x + 6 cosx at the point (π/3, π + 3). (b) Illustrate part (a) by graphing the curve an) the tangent line on the same screen.
> For what values of x does the graph of f have a horizontal tangent? f (x) = x + 2 sin x
> Lake Lanier in Georgia, USA, is a reservoir created by Buford Dam on the Chattahoochee River. The table shows the rate of inflow of water, in cubic feet per second, as measured every morning at 7:30 am by the US Army Corps of Engineers. Use the Midpoint
> Find an equation of the tangent line to the curve at the given point. y = cos x - sin x, (π, -1)
> Find an equation of the tangent line to the curve at the given point. y = ex cos x, (0, 1)
> Find f ’ (x) and f ’’ (x). f(x) = x2 / 1+ex
> Find an equation of the tangent line to the curve at the given point. y = sin x + cos x, (0, 1)
> Prove, using the definition of derivative, that if f (x) = cos x, then f ‘(x) = -sin x.
> Find dy/dx by implicit differentiation. ey sin x = x + xy
> Explain exactly what is meant by the statement that “differentiation and integration are inverse processes.”
> Differentiate. f (t) = tet cot t
> The area labeled B is three times the area labeled A. Express b in terms of a. yA y. y= e* y=e* A B a
> Let (a) Find an expression for g(x) similar to the one for f (x). (b) Sketch the graphs of f and g. (c) Where is f differentiable? Where is t differentiable? if x <0 f(x) = 2 if 0 <x<1 - x if 1<x<2 if x > 2 g(x) = f(t) dt
> Justify (3) for the case h (3): f(u) < g(x + h) – g(x) < f(v) h 3.
> Differentiate. f (θ) = cosθ sinθ
> A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 420. (a) Find an expression for the number of bacteria after t hours. (b) Find the number of bacteria after 3 hour
> What is wrong with the equation? sec?x dx = tan. x - = 0 11
> What is wrong with the equation? sec 0 tan 0 d0= sec 0 = -3 T/3 /3
> What is wrong with the equation? 2 4 dx = 3 x? 2 -1
> Differentiate. y = cos x / 1 - sin x
> What is wrong with the equation? -3 3 -3 -2 8 -2
> The acceleration function (in m/s2 ) and the initial velocity are given for a particle moving along a line. Find (a) the velocity at time t and (b) the distance traveled during the given time interval. a(t) = t + 4, v(0) = 5, 0 ≤ t ≤ 10
> (a) Find an equation of the tangent line to the curve y = 2x sin x at the point (π/2, π). (b) Illustrate part (a) by graphing the curve and the tangent line on the same screen.
> The velocity function (in meters per second) is given for a particle moving along a line. Find (a) the displacement and (b) the distance traveled by the particle during the given time interval. v(t) = t2 - 2t – 3, 2 ≤ t ≤ 4

