Question:
(a) Based on the R2 and ANOVA table for your model, how would you assess the fit? (b) Interpret the p-value for the F statistic. (c) Would you say that your model’s fit is good enough to be of practical value?
Midterm and Final Exam Scores for Business Statistics Students Fall Semester 2011 (n = 58 students)
Midterm Exam Score ………………………………………………… Final Exam Score
80 ……………………………………………………………………………………………………. 78
87 ……………………………………………………………………………………………………. 85
72 ……………………………………………………………………………………………………. 81
80 ……………………………………………………………………………………………………. 82
68 ……………………………………………………………………………………………………. 70
73 ……………………………………………………………………………………………………. 69


Transcribed Image Text:
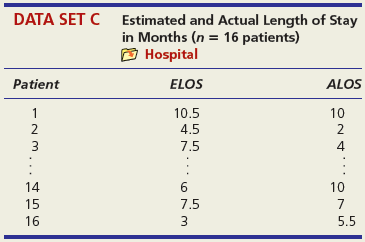
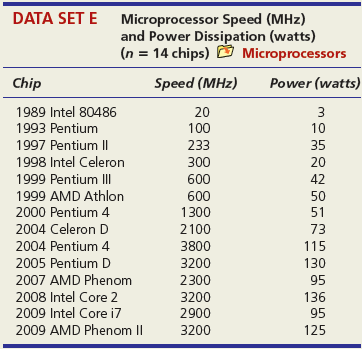
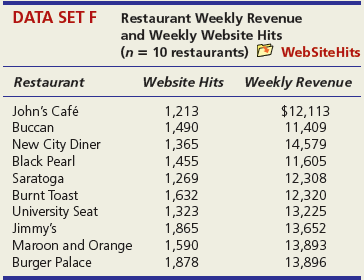
DATA SET A Median Income and Median Home Prices by State (n = 51 states) O HomePrice3 State Median Income Median Price $40,933 57,848 46,896 $241,750 128,969 120,560 AK AL AR 42,777 50,351 52,201 WI 153,935 129,369 183,202 wV WY DATA SET C Estimated and Actual Length of Stay in Months (n = 16 patients) O Hospital Patient ELOS ALOS 1 10.5 10 2 4.5 2 3. 7.5 4 14 10 15 7.5 7 16 5.5 ONM ... DATA SET D Single-Engine Aircraft Performance (n = 52 airplanes) O Airplanes Mfgr/Model TotalHP Cruise AMD CH 2000 116 100 Beech Baron 58 Beech Baron 58P 600 200 650 241 Sky Arrow 650 TC Socata TB20 Trinidad 81 98 250 163 Tiger AG-5B 180 143 DATA SET E Microprocessor Speed (MHz) and Power Dissipation (watts) (n = 14 chips) O Microprocessors Chip Speed (MHz) Power (watts) 1989 Intel 80486 20 3 1993 Pentium 100 10 1997 Pentium I| 1998 Intel Celeron 233 35 300 20 1999 Pentium III 600 42 1999 AMD Athlon 600 50 2000 Pentium 4 1300 51 2004 Celeron D 2100 73 2004 Pentium 4 3800 115 2005 Pentium D 2007 AMD Phenom 3200 130 2300 95 2008 Intel Core 2 2009 Intel Core i7 3200 136 2900 95 2009 AMD Phenom II 3200 125 DATA SET F Restaurant Weekly Revenue and Weekly Website Hits (n = 10 restaurants) D WebSiteHits Restaurant Website Hits Weekly Revenue 1,213 1,490 1,365 1,455 1,269 1,632 1,323 1,865 1,590 1,878 John's Café $12,113 11,409 14,579 11,605 12,308 12,320 13,225 13,652 13,893 13,896 Buccan New City Diner Black Pearl Saratoga Burnt Toast University Seat Jimmy's Maroon and Orange Burger Palace Mileage and Vehicle Weight DATA SET G (n = 73 vehicles) E MPG2 Vehicle Weight City MPG Acura TL 3968 20 Audi A5 3583 22 BMW 4 Series 428i 3470 22 Volkswagen Passat SE Volvo S60 T5 3230 24 3528 21 Volvo XC90 4667 16 DATA SET H Pasta Sauce per Gram Total Calories and Fat Calories (n = 20 products) O Pasta Product Fat Cal/gm Cal/gm Barilla Roasted Garlic & Onion 0.20 0.64 Barilla Tomato & Basil 0.12 0.56 Classico Tomato & Basil 0.08 0.40 Ragu Roasted Garlic Ragu Traditional Sutter Home Tomato & Garlic 0.19 0.70 0.20 0.56 0.16 0.64 DATA SET I Temperature and Energy Usage for a Residence (n = 24 months) O Electric Month Avg Temp (F°) Usage (kWh) 1 62 436 2 71 464 3 76 446 22 25 840 23 38 867 24 48 606 U.S. Annual Percent Inflation in Prices of Commodities and Services DATA SET J (n = 47 years) Inflation Year Commodities% Services% 1960 0.9 3.4 1961 0.6 1.7 1962 0.9 2.0 2004 2.3 2.9 2005 3.6 3.3 2006 2.4 3.8
> In a test of the regression model Y = β0 + β1X with 27 observations, what is the critical value of t to test the hypothesis that β1 = 0 using α = .05 in a two-tailed test? a. 1.960 b. 2.060 c. 1.708
> Based on the information in this ANOVA table, the coefficient of determination R2 is a. 0.499 b. 0.501 c. 0.382 ANOVA Table Source Sum of Squares df Mean Square F p-Value 158.3268 Regression Residual 1 158.3268 24.88 0.00004 159.0806 25 6.3632 To
> Which statement is incorrect? Explain. a. Correlation uses a t-test with n - 2 degrees of freedom. b. Correlation analysis assumes that X is independent and Y is dependent. c. Correlation analysis is a test for the degree of linearity between X and Y.
> Given a sample correlation coefficient r = .373 with n = 30, can you reject the hypothesis ρ = 0 for the population at α = .01? Explain, stating the critical value you are using in the test.
> Given the following ANOVA: (a). How many ATM locations were there? (b). What was the sample size? (c). At α = .05, is there a significant effect due to Day of Week? (d). At α = .05, is there a significant interaction?
> If P (A) = .30, P (B) = .70, and P (A ∩ B) = .25, are A and B independent events? Explain.
> Given the following ANOVA table, find the F statistic and the critical value of F.05. Source Sum of Squares df Mean Square F Treatment 744.00 4. Error 751.50 15 Total 1,495.50 19
> Which statement is incorrect? Explain. a. We need a Tukey test because ANOVA doesn’t tell which group means differ. b. Hartley’s test is needed to determine whether the means of the groups differ. c. ANOVA assumes equal variances in the k groups being c
> In this regression with n = 40, which predictor differs significantly from zero at α = .01? a. X2 b. X3 c. X5 Coefficients Std. Error Intercept 3.210610 0.918974 X1 -0.034719 0.023283 X2 0.026794 0.039741 X3 -0.048533 0.000272 0.009
> Which predictors differ significantly from zero at α = .05? a. X3 only b. X4 only c. both X3 and X4 Coefficients Std. Error p-Value Intercept X1 23.3015 4.1948 0.0000 0.2100 -0.227977 0.178227 X2 0.218970 0.300784 0.4719 X3 -0.34365
> Which predictor coefficients differ significantly from zero at α = .05? a. X3 and X5 b. X5 only c. all but X1 and X3 Coefficients Std. Error Lower 95% Upper 95% Intercept 22.47427 6.43282 9.40122 35.54733 X1 -0.243035 0.162983 -0.57
> For a multiple regression, which statement is false? Explain. a. If R2 = .752 and R2 adj = .578, the model probably has at least one weak predictor. b. R2 adj can exceed R2 if the model contains some very strong predictors. c. Deleting a predictor could
> (a) Plot the data on skier/snowboard visits. (b) Would a fitted trend be helpful? Explain. (c) Make a forecast for 2007–2008, using a trend model of your choice (or a judgment forecast). U.S. Skier/Snowboarder Visits, 1984-2007 (mi
> The process that produces Sonora Bars (a type of candy) is intended to produce bars with a mean weight of 56 grams (g). The process standard deviation is known to be 0.77 g. A random sample of 49 candy bars yields a mean weight of 55.82 g. (a). State t
> Given H0: μ > 18 and H1: μ < 18, we would commit Type I error if we a. conclude that μ > 18 when the truth is that μ < 18. b. conclude that μ < 18 when the truth is that μ > 18. c. fail to reject μ > 18 when the truth is that μ < 18.
> Given n1 = 8, s1 = 14, n2 = 12, s2 = 7. (a). Find the test statistic for a test for equal population variances. (b). At α = .05 in a two-tailed test, state the critical value and degrees of freedom.
> For the following contingency table, find (a) P (H ∩ T); (b) P (S | G); (c) P(S) R Row Total 10 50 30 90 H 20 50 40 110 Col Total 30 100 70 200
> Which statement is correct concerning the normal approximation? Why not the others? a. The normal Poisson approximation is acceptable when λ > 10. b. The normal binomial approximation is better when n is small and π is large. c. Normal approximations are
> In a random sample of 200 Colorado residents, 150 had skied at least once last winter. A similar sample of 200 Utah residents revealed that 140 had skied at least once last winter. At α = .025, is the percentage significantly greater in Colorado? Explain
> Which of the following Excel formulas would be a correct way to calculate P(X < 450) given that X is N(500, 60)? a. =NORM.DIST(450, 500, 60, 1) b. =NORM.S.DIST(450, 60) c. =1–NORM.DIST(450, 500, 60, 0)
> A consulting firm used a random sample of 12 CIOs (chief information officers) of large businesses to examine the relationship (if any) between salary (in thousands) and years of service in the firm. (a). Make a scatter plot and describe it. (b). Calc
> Five students in a large lecture class compared their scores on two exams. “Looks like the class mean was higher on the second exam,” Bob said. (a). What kind of test would you use? (b). At α = .10, w
> Find the mean, standard deviation, and coefficient of variation for X = 5, 10, 20, 10, 15.
> Which statement is incorrect? Explain. a. If p = .50 and n = 100, the estimated standard error of the sample proportion is .05. b. In a sample size calculation for estimating π, it is conservative to assume π = .50. c. If n = 250 and p = .07 it is not s
> Which statement is false? Explain. a. To find probabilities in a continuous distribution, we add up the probabilities at each point. b. A uniform continuous model U(5,21) has mean 13 and standard deviation 4.619. c. A uniform PDF is constant for all valu
> A sample of 9 customers in the “quick” lane in a supermarket showed a mean purchase of $14.75 with a standard deviation of $2.10. (a) Find the 95 percent confidence interval for the true mean. (b) Why should you use t instead of z in this case?
> A sample of 16 ATM transactions shows a mean transaction time of 67 seconds with a standard deviation of 12 seconds. (a). State the hypotheses to test whether the mean transaction time exceeds 60 seconds. (b). Find the test statistic. (c). At α = .02
> Which statement is not correct? Explain. a. The sample data x1, x2, . . . , xn will be approximately normal if the sample size n is large. b. For a skewed population, the distribution of / is approximately normal if n is large. c. The expected value of /
> A regression model to predict Y, the state burglary rate per 100,000 people for 2005, used the following four state predictors: X1 = median age in 2005, X2 = number of 2005 bankruptcies, X3 = 2004 federal expenditures per capita (a leading predictor), an
> A random sample of 502 Vail Resorts’ guests were asked to rate their satisfaction on various attributes of their visit on a scale of 1–5 with 1 = very unsatisfied and 5 = very satisfied. The regression model was Y = ov
> A sample of 74 Noodles & Company restaurants was used to perform a regression analysis with Y = % Annual Revenue Growth and X = % Revenue Due to Loyalty Card Use. Calculate the leverage statistic for the following three restaurants and state whether or n
> A sample of season performance measures for 29 NBA teams was collected for a season. A regression analysis was performed on two of the variables with Y = total number of free throws made and X = total number of free throws attempted. Calculate the levera
> An estimated regression for a random sample of vehicles is MPG = 49.22 - 0.081 Horsepower, where MPG is miles per gallon and Horsepower is the engine’s horsepower. The standard error is se = 2.03. Suppose an engine has 200 horsepower and its actual (obse
> Observations are taken on net revenue from sales of a certain LCD TV at 50 retail outlets. The regression model was Y = net revenue (thousands of dollars), X1 = shipping cost (dollars per unit), X2 = expenditures on print advertising (thousands of dollar
> In the previous problem, calculate (a) the 95th percentile of vehicle speeds (i.e., 95 percent below); (b) the lowest 10 percent of speeds; (c) the highest 25 percent of speeds (3rd quartile).
> (a) Make an Excel scatter plot. What does it suggest about the population correlation between X and Y? (b) Make an Excel worksheet to calculate SSxx, SSyy, and SSxy. Use these sums to calculate the sample correlation coefficient. Check your work by using
> Review the two residual plots below. Do either of these show evidence that the regression error assumptions of normality and constant variation have been violated? Explain. X -3.0 -2.0 -1.0 0.0 1.0 2.0 3.0 Normal Score Residual Residuals
> Review the two residual plots below. Do either of these show evidence that the regression error assumptions of normality and constant variation have been violated? Explain. -3.0 -2.0 -1.0 0.0 1.0 2.0 3.0 Normal Score Residual
> Study the table of residuals. Identify as outliers any standardized residuals that exceed 3 and as unusual any that exceed 2. Can you suggest any reasons for these unusual residuals? Midterm and Final Exam Scores for Business Statistics Students Fall S
> Refer to the Revenue and Profit data set below. Data are in billions of dollars. (a) Use MegaStat or MINITAB to find confidence and prediction intervals for Y using the following set of x values: 1.8, 15, and 30. (b) Report the 95 percent confidence inte
> Refer to the Weekly Earnings data set below. (a) Use MegaStat or MINITAB to find confidence and prediction intervals for Y using the following set of x values: 12, 17, 21, 25, and 30. (b) Report the 95 percent confidence interval and prediction interval
> (a) Use Excel’s Data Analysis > Regression (or MegaStat or MINITAB) to obtain regression estimates. (b) Interpret the 95 percent confidence interval for the slope. Does it contain zero? (c) Interpret the t test for the slope and its p-value. (d) Interpre
> (a) Use Excel’s Data Analysis > Regression (or MegaStat or MINITAB) to obtain regression estimates. (b) Interpret the 95 percent confidence interval for the slope. Does it contain zero? (c) Interpret the t test for the slope and its p-value. (d) Interpre
> (a) Use Excel’s Data Analysis > Regression (or MegaStat or MINITAB) to obtain regression estimates. (b) Interpret the 95 percent confidence interval for the slope. Does it contain zero? (c) Interpret the t test for the slope and its
> Below is a regression using X = average price, Y = units sold, n = 20 stores. (a) Write the fitted regression equation. (b) Write the formula for each t statistic and verify the t statistics shown below. (c) State the degrees of freedom for the t tests a
> Below is a regression using X = home price (000), Y = annual taxes (000), n = 20 homes. (a) Write the fitted regression equation. (b) Write the formula for each t statistic and verify the t statistics shown below. (c) State the degrees of freedom for the
> A regression was performed using data on 16 randomly selected charities. The variables were Y = expenses (millions of dollars) and X = revenue (millions of dollars). (a) Write the fitted regression equation. (b) Construct a 95 percent confidence interval
> Which probability distribution (uniform, binomial, Poisson) is most nearly appropriate to describe each situation (assuming you knew the relevant parameters)? a. The number of dimes older than 10 years in a random sample of 8 dimes. b. The number of hos
> A regression was performed using data on 32 NFL teams. The variables were Y = current value of team (millions of dollars) and X = total debt held by the team owners ( millions of dollars). (a) Write the fitted regression equation. (b) Construct a 95 perc
> (a) Perform a regression using MegaStat or Excel. (b) State the null and alternative hypotheses for a two-tailed test for a zero slope. (c) Report the p-value and the 95 percent confidence interval for the slope shown in the regression results. (d) Is th
> (a) Perform a regression using MegaStat or Excel. (b) State the null and alternative hypotheses for a two-tailed test for a zero slope. (c) Report the p-value and the 95 percent confidence interval for the slope shown in the regression results. (d) Is th
> Using the “Metals” data, construct a correlation matrix of the six independent variables. The response variable is Priceylb. (a). Identify any pairs of independent variables that have a significant pairwise correlation. (b). Using MegaStat or MINITAB,
> (a) Use Excel to make a scatter plot of the data. (b) Select the data points, right-click, select Add Trendline, select the Options tab, and choose Display equation on chart and Display R-squared value on chart. (c) Interpret the fitted slope. (d) Is the
> (a) Use Excel to make a scatter plot of the data. (b) Select the data points, right-click, select Add Trendline, select the Options tab, and choose Display equation on chart and Display R-squared value on chart. (c) Interpret the fitted slope. (d) Is the
> (a) Make an Excel worksheet to calculate SSxx, SSyy, and SSxy (the same worksheet you used in exercises 12.2 and 12.3). (b) Use the formulas to calculate the slope and intercept. (c) Use your estimated slope and intercept to make a worksheet to calculate
> (a) Make an Excel worksheet to calculate SSxx, SSyy, and SSxy (the same worksheet you used in exercises 12.2 and 12.3). (b) Use the formulas to calculate the slope and intercept. (c) Use your estimated slope and intercept to make a worksheet to calculate
> Refrigerator prices are affected by characteristics such as whether or not the refrigerator is on sale, whether or not it is listed as a Sub-Zero brand, the number of doors (one door or two doors), and the placement of the freezer compartment (top, side,
> A regression model to predict the price of diamonds included the following predictor variables: the weight of the stone (in carats where 1 carat = 0.2 gram), the color rating (D, E, F, G, H, or I), and the clarity rating (IF, VVS1, VVS2, VS1, or VS2). (
> Which statement is false? Explain. a. If μ = 52 and σ = 15, then X = 81 would be an outlier. b. If the data are from a normal population, about 68 percent of the values will be within μ ± σ. c. If μ = 640 and σ = 128 then the coefficient of variation is
> (a) Does the 95 percent confidence interval for the slope include zero? If so, what does this tell you? If not, what does it mean? (b) Do a two-tailed t test for zero slope at α = .05. State the hypotheses, degrees of freedom, and critical
> Below are fitted regressions for Y = asking price of a used vehicle and X = the age of the vehicle. The observed range of X was 1 to 8 years. The sample consisted of all vehicles listed for sale in a particular week. (a) Interpret the slope of each fitte
> The regression equation Credits = 15.4 -.07 Work was estimated from a sample of 21 statistics students. Credits is the number of college credits taken and Work is the number of hours worked per week at an outside job. (a). Interpret the slope. (b). Is
> The regression equation HomePrice = 51.3 + 2.61 Income was estimated from a sample of 34 cities in the eastern United States. Both variables are in thousands of dollars. HomePrice is the median selling price of homes in the city, and Income is median fam
> The regression equation NetIncome = 2,277 + .0307 Revenue was estimated from a sample of 100 leading world companies (variables are in millions of dollars). (a). Interpret the slope. (b). Is the intercept meaningful? Explain. (c). Make a prediction o
> (a) Interpret the slope of the fitted regression Number of International Franchises = -47.5 + 1.75 Power Distance Index. The Power Distance Index is a measure on a scale of 0–100 of the wealth gap between the richest and poorest in a country. (b) What is
> Observations are taken on sales of a certain mountain bike in 30 sporting goods stores. The regression model was Y = total sales (thousands of dollars), X1 = display floor space (square meters), X2 = competitors’ advertising expenditure
> Observations are taken on net revenue from sales of a certain LCD TV at 50 retail outlets. The regression model was Y = net revenue (thousands of dollars), X1 = shipping cost (dollars per unit), X2 = expenditures on print advertising (thousands of dollar
> Refer to the ANOVA table below. (a) State the degrees of freedom for the F test for overall significance. (b) Use Appendix F to look up the critical value of F for α = .05. (c) Calculate the F statistic. Is the regression significant overal
> (a) Make a scatter plot of the data. What does it suggest about the correlation between X and Y? (b) Use Excel, MegaStat, or MINITAB to calculate the correlation coefficient. (c) Use Excel or Appendix D to find t.025 for a two-tailed test at Î&plu
> (a) Make an Excel scatter plot. What does it suggest about the population correlation between X and Y? (b) Make an Excel worksheet to calculate SSxx, SSyy, and SSxy. Use these sums to calculate the sample correlation coefficient. Check your work by using
> Use Excel, MegaStat, or MINITAB to fit the regression model, including residuals and standardized residuals. Midterm and Final Exam Scores for Business Statistics Students Fall Semester 2011 (n = 58 students) Midterm Exam Score …&ac
> Which statement is true? Why not the others? a. We expect the median to exceed the mean in positively skewed data. b. The geometric mean is not possible when there are negative data values. c. The midrange is resistant to outliers.
> For each sample, do a test for zero correlation. (a) Use Appendix D to find the critical value of tα. (b) State the hypotheses about ρ. (c) Perform the t test and report your decision. Appendix D: a. r = +.45, n = 20, Î&
> A box of Wheat Chex cereal is to be filled to a mean weight of 466 grams. The lower specification limit is 453 grams (the labeled weight is 453 grams) and the upper specification limit is 477 grams (so as not to overfill the box). The process standard de
> A new type of smoke detector battery is developed. From laboratory tests under standard conditions, the half-life (defined as less than 50 percent of full charge) of 20 batteries are shown below. (a). Make a histogram of the data and/or a probability p
> A Nabisco Fig Newton has a process mean weight of 14.00 g with a standard deviation of 0.10 g. The lower specification limit is 13.40 g and the upper specification limit is 14.60 g. (a). Describe the capability of this process, using the techniques you
> Refer to the freezer data’s 80 individual temperature observations in problem 17.52. Problem 17.52: Refer to the freezer problem 17.51 with μ = 23 and σ = 2. Temperature measurements are recorded four times a
> The temperature control unit on a commercial freezer in a 24-hour grocery store is set to maintain a mean temperature of 23 degrees Fahrenheit. The temperature varies because people are constantly opening the freezer door to remove items, but the thermos
> Refer back to Table 15.11, which shows the distribution of the number of U.S. Supreme Court appointments per year from 1900–1999. Since 1999 there have been four Supreme Court appointments with one each in the years 2005, 2006, 2009, an
> (a) Use Excel’s Data Analysis > Random Numbers to generate 100 Poisson-distributed random numbers with a mean of λ = 4. (b) Make a histogram of your sample and assess its shape. (c) Calculate descriptive statistics. Are
> (a) Use Excel’s function =RAND() or Excel’s Data Analysis > Random Numbers to generate 100 uniformly distributed random numbers between 0 and 1. (b) Make a histogram of your sample and assess its shape. (c) Calculat
> Interpret the slope. Does the intercept have meaning, given the range of the data? Midterm and Final Exam Scores for Business Statistics Students Fall Semester 2011 (n = 58 students) Midterm Exam Score ……â&
> (a) Use Excel’s function =NORM.INV(RAND(),0,1) or Excel’s Data Analysis > Random Numbers to generate 100 normally distributed random numbers with a mean of 0 and a standard deviation of 1. (b) Make a histogram of yo
> If a random experiment whose success probability is .20 is repeated 8 times, find the probability of (a) exactly 3 successes; (b) more than 3 successes; (c) at most 2 successes. (d) Which probability distribution did you use and why?
> Using test data on 43 vehicles, an analyst fitted a regression to predict CityMPG (miles per gallon in city driving) using as predictors Length (length of car in inches), Width (width of car in inches), and Weight (weight of car in pounds). Interpret the
> Analysis of a Detroit Marathon (n = 1,015 men, n = 150 women) produced the regression results shown below, with dependent variable Time (the marathon time in minutes) and predictors Age (runner’s age), Weight (runner’s
> An expert witness in a case of alleged racial discrimination in a state university school of nursing introduced a regression of the determinants of Salary of each professor for each year during an 8-year period (n = 423) with the following results, with
> A sports enthusiast created an equation to predict Victories (the team’s number of victories in the National Basketball Association regular season play) using predictors FGP (team field goal percentage), FTP (team free throw percentage)
> A researcher used stepwise regression to create regression models to predict Birth Rate (births per 1,000) using five predictors: LifeExp (life expectancy in years), InfMort (infant mortality rate), Density (population density per square kilometer), GDPC
> Using test data on 20 types of laundry detergent, an analyst fitted a regression to predict Cost Per Load (average cost per load in cents per load) using binary predictors Top Load (1 if washer is a top loading model, 0 otherwise) and Powder (if detergen
> A hospital emergency room analyzed n = 17,664 hourly observations on its average occupancy rates using six binary predictors representing days of the week and two binary predictors representing the 8-hour work shift (12 a.m.–8 a.m., 8 a.m.–4 p.m., 4 p.m.
> In a study of paint peel problems, a regression was suggested to predict defects per million (the response variable). The intended predictors were supplier (four suppliers, coded as binaries) and substrate (four materials, coded as binaries). There were
> Which one of the following is true? Why not the others? a. Histograms are useful for visualizing correlations. b. Pyramid charts are generally preferred to bar charts. c. A correlation coefficient can be negative.
> In a model of Ford’s quarterly revenue Total Revenue = β0 + β1 Car Sales + β2 Truck Sales + β3 SUVSales + ε, the three predictors are measured in number of units sold (not dollars). (a). Interpret each slope. (b). Would the intercept be meaningful? (c)
> If you are using time-series data, perform one or more tests for autocorrelation (visual inspection of residuals plotted against observation order, runs test, Durbin-Watson test). Is autocorrelation a concern? DATA SET A Mileage and Other
> Here are the ages of a random sample of 20 CEOs (chief executive officers) of Fortune 500 U.S. corporations. (a). Find the mean, median, and mode. (b). Discuss advantages and disadvantages of each of these measures of center for this data set. (c). F
> If you did not already do so, request a plot of residuals versus the fitted Y. Is heteroscedasticity a concern? DATA SET A Mileage and Other Characteristics of Randomly Selected Vehicles (n = 73, k = 4) O Mileage Obs Vehicle CityMPG Length
> If you did not already do so, request a histogram of standardized residuals and/or a normal probability plot. Do the residuals suggest non-normal errors? Explain. DATA SET A Mileage and Other Characteristics of Randomly Selected Vehicles (
> If you did not already do so, request leverage statistics. Are any observations influential? Explain. DATA SET A Mileage and Other Characteristics of Randomly Selected Vehicles (n = 73, k = 4) O Mileage Obs Vehicle CityMPG Length Width Wei
> (a). If you did not already do so, request a table of standardized residuals. (b). Are any residuals outliers (three standard errors) or unusual (two standard errors)? DATA SET A Mileage and Other Characteristics of Randomly Selected Vehi

