Question: A community of 10,000 people is
A community of 10,000 people is homogeneously mixed. One person who has just returned from another community has influenza. Assume that the home community has not had influenza shots and all are susceptible. One mathematical model assumes that influenza tends to spread at a rate in direct proportion to the number N who have the disease and to the number 10,000 - N who have not yet contracted the disease (logistic growth). Mathematically,
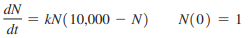
where N is the number of people who have contracted influenza after t days. For k = 0.0004, N(t) is the logistic growth function.
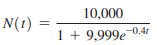
(A) How many people have contracted influenza after 1 week? After 2 weeks?
(B) How many days will it take until half the community has contracted influenza?
(C) Find limtS∞ N(t).
(D) Graph N = N(t) for 0 ≤ t ≤ 50.
> Use a graphing calculator to approximate the limiting matrix for the indicated standard form.
> perform a mental calculation to find the answer and include the correct units. Find the total area enclosed by 6 non-overlapping rectangles, if each rectangle is 10 centimeters high and 3 centimeters wide.
> For the data in Problem 77, use left and right sums over three equal subintervals to approximate the area under the graph of N′(x) from x = 0 to x = 6. Replace the question marks with values of L3 and R3 as appropriate: Data from Probl
> Refer to Problem 75. Use left and right sums over five equal subintervals to approximate the area under the graph of A′(t) from t = 5 to t = 10. Calculate an error bound for this estimate. Data From Problem 75: The rate of healing, A&a
> For a new employee in Problem 73, use left and right sums to estimate the area under the graph of N(t) from t = 20 to t = 100. Use four equal subintervals for each. Replace the question marks with the values of L4 or R4 as appropriate:
> The left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)
> the left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)
> use derivatives to determine whether f is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.
> Use derivatives to determine whether  is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.
> Use L5 and R5 to approximate Compute error bounds for each. (Round answers to two decimal places.) Describe in geometric terms what the definite integral over the interval [1, 6] represents.
> Refer to the following figure showing two parcels of land along a river: Refer to Problem 61. Use R10 to estimate the combined area of both parcels, and calculate an error bound for this estimate. How many subdivisions of the baseline would
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is regular, then it is absorbing.
> could the given matrix be the transition matrix of an absorbing Markov chain?
> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If ƒ is a decreasing function on [a, b], then the area under the graph of is greater than the left sum Ln and less th
> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If (x)= 2x on [0, 10] and n is a positive integer, then there is some Riemann sum Sn that equals the exact area under
> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample.
> calculate the definite integral, given that
> calculate the definite integral, given that
> calculate the definite integral, given that
> calculate the definite integral, given that
> calculate the definite integral, given that
> calculate the definite integral, given that
> calculate the definite integral by referring to the figure with the indicated areas.
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is absorbing, then it has a unique stationary matrix.
> calculate the definite integral by referring to the figure with the indicated areas.
> calculate the definite integral by referring to the figure with the indicated areas.
> calculate the definite integral by referring to the figure with the indicated areas.
> calculate the definite integral by referring to the figure with the indicated areas.
> calculate the definite integral by referring to the figure with the indicated areas.
> calculate the indicated Riemann sum Sn for the function (x) = x2 - 5x - 6. Partition 31, 74 into six subintervals of equal length, and let c1 = 2, c2 = 2, c3 = 4, c4 = 4, c5 = 6, and c6 = 6.
> calculate the indicated Riemann sum Sn for the function (x) = x2 - 5x - 6. Partition 30, 34 into three subintervals of equal length, and let c1 = 0.2, c2 = 1.5, and c3 = 2.8.
> calculate the indicated Riemann sum Sn for the function (x) = 25 - 3x2 . Partition 3-5, 54 into five subintervals of equal length, and for each subinterval [xk - 1, xk], let ck = (xk - 1 + xk) /2.
> calculate the indicated Riemann sum Sn for the function (x) = 25 - 3x2 . Partition 30, 124 into four subintervals of equal length, and for each subinterval [xk - 1, xk], let ck = (xk - 1 + 2xk) /3.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Compute error bounds for L3 and R3 found in Problem 18 for both figures.
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain has exactly three states, one nonabsorbing and two absorbing, then it is an absorbing chain.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Replace the question marks with L3 and R3 as appropriate. Explain your choice.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Using the results of Problem 16, compute L3 and R3 for Figure C and for Figure D.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Draw in left and right rectangles for Figures C and D.
> Refer to the rectangles F, G, H, I, and J in the following figure. Which rectangles are neither left nor right rectangles?
> Refer to the rectangles F, G, H, I, and J in the following figure. Which rectangles are left rectangles?
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain has exactly two states and at least one absorbing state, then it is an absorbing chain.
> The Weber–Fechner law concerns a person’s sensed perception of various strengths of stimulation involving weights, sound, light, shock, taste, and so on. One form of the law states that the rate of change of sensed sen
> For a person learning to type, the number N of words per minute that the person could type after t hours of practice was given by the limited growth function N = 1001(1 - e-0.02t ) What is the rate of improvement after 10 hours of practice? After 40 ho
> Many countries have banned the use of the insecticide DDT because of its long-term adverse effects. Five years after a particular country stopped using DDT, the amount of DDT in the ecosystem had declined to 70% of the amount present at the time of the b
> Under certain assumptions, the blood pressure P in the largest artery in the human body (the aorta) changes between beats with respect to time t according to where a is a constant. Find P = P(t) that satisfies both conditions
> A company is trying to expose a new product to as many people as possible through online ads. Suppose that the rate of exposure to new people is proportional to the number of those who have not seen the product out of L possible viewers (limited growth).
> The marginal price dp/dx at x units of supply per day is proportional to the price p. There is no supply at a price of $20 per unit [p(0) = 20], and there is a daily supply of 40 units at a price of $23.47 per unit [p(40) = 23.47]. (A) Find the price–su
> Find the amount A in an account after t years if
> Find the amount A in an account after t years if
> Refer to Problem 75. Explain why the world population function Q(t) does not satisfy an exponential growth law. Data from Problem 75: Let Q(t) denote the population of the world at time t. In 1999, the world population was 6.0 billion and increasing at
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Find the value of t for which the logistic function is equal to M/2.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> Show that y = 2/ (1 + ce-6t) is a solution of the differential equation dy/dt = 3y(2 – y) for any real number c. Find the particular solution that passes through (0, 1).
> Show that y = C/x is a solution of the differential equation dy/dx = -y/x for any real number C. Find the particular solution that passes through (2, 5).
> Show that y = √x2 + C is a solution of the differential equation dy/dx = x/y for any real number C. Find the particular solution that passes through (-6, 7).
> Refer to the following slope fields: Use a graphing calculator to graph y = Cex - 1 for C = -2, -1, 1, and 2, for -5 ≤ x ≤ 5, -5 ≤ y ≤ 5, all in the same viewing window. Obse
> Refer to the following slope fields: Graph the particular solution found in Problem 54 in the appropriate Figure A or B (or a copy).
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Refer to the following slope fields: Show that y = Ce x- 1 is a solution of the differential equation dy/dx = y + 1 for any real number C. Find the particular solution that passes through (0, 0).
> Refer to the following slope fields: Which slope field is associated with the differential equation dy/dx = y + 1? Briefly justify your answer.
> does the given differential equation model unlimited growth, exponential decay, limited growth, or logistic growth? y(= 10,000 - y
> does the given differential equation model unlimited growth, exponential decay, limited growth, or logistic growth? y(= -0.0152y
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Refer to the following slope fields: Graph the particular solution found in Problem 36 in the appropriate Figure A or B (or a copy).
> Refer to the following slope fields: Solve the differential equation dy/dx = -x and find the particular solution that passes through (0, 3).
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Refer to the following slope fields: Which slope field is associated with the differential equation dy/dx = -x? Briefly justify your answer.
> Is y = e-3x a solution of the differential equation y( - 4y( + 3y = 0? Explain.
> Is y = -2ex a solution of the differential equation y’’ - 4y= + 3y = 0? Explain.
> Is y = 5ex2/2 a solution of the differential equation y’= xy? Explain.
> Is y = 8x + 8 a solution of the differential equation
> Give the order (first, second, third, etc.) of each differential equation, where y represents a function of the variable.
> Give the order (first, second, third, etc.) of each differential equation, where y represents a function of the variable.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> find the limiting matrix for the indicated standard form. Find the long-run probability of going from each nonabsorbing state to each absorbing state and the average number of trials needed to go from each nonabsorbing state to an absorbing state.
> The function x(t) in Problem 95 exhibits logistic growth. Why might the rate at which a rumor spreads initially increase, but eventually slow down? Data from Problem 95:
> Find the general or particular solution, as indicated, for each first-order differential equation.
> A college language class was chosen for an experiment in learning. Using a list of 50 words, the experiment involved measuring the rate of vocabulary memorization at different times during a continuous 5-hour study session. It was found that the average
> Find the general or particular solution, as indicated, for each first-order differential equation.
> The area A of a healing wound changes at a rate given approximately by where t is time in days and A(1) = 2 square centimeters. What will the area of the wound be in 10 days?
> An average student enrolled in a steno typing class progressed at a rate of N′(t) = 12e-0.06t words per minute per week t weeks after enrolling in a 15-week course. If, at the beginning of the course, a student could stenotype at zero words per minute,
> If the rate of labor use in Problem 89 is L′(x) = 2,000x-1/3 and if the first 8 control units require 12,000 labor-hours, how many labor-hours, L(x), will be required for the first x control units? The first 27 control units?
> An oil tanker aground on a reef is losing oil and producing an oil slick that is radiating outward at a rate given approximately by where R is the radius (in feet) of the circular slick after t minutes. Find the radius of the slick after 16 minutes if
> Repeat Problem 86 if S′(t) = 500t1/4 + 300 and all other information remains the same. Use a graphing calculator to approximate the solution of the equation S(t)= 20,000 to two decimal places. Data from Problem 86: The rate of change of the monthly sale
> The rate of healing for a skin wound (in square centimeters per day) is approximated by A′(t) = -0.9e-0.1t If the initial wound has an area of 7 square centimeters, what will its area A(t) be after t days? After 5 days?
> find the limiting matrix for the indicated standard form. Find the long-run probability of going from each nonabsorbing state to each absorbing state and the average number of trials needed to go from each nonabsorbing state to an absorbing state.

