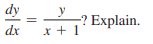Question: Is y = 8x + 8 a solution of
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain has exactly three states, one nonabsorbing and two absorbing, then it is an absorbing chain.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Replace the question marks with L3 and R3 as appropriate. Explain your choice.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Using the results of Problem 16, compute L3 and R3 for Figure C and for Figure D.
> Involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals. Draw in left and right rectangles for Figures C and D.
> Refer to the rectangles F, G, H, I, and J in the following figure. Which rectangles are neither left nor right rectangles?
> Refer to the rectangles F, G, H, I, and J in the following figure. Which rectangles are left rectangles?
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> Express the relationship between = (x) and (x) in words, and write a differential equation that (x) satisfies. For example, the derivative of (x) = e3x is 3 times ï
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain has exactly two states and at least one absorbing state, then it is an absorbing chain.
> The Weber–Fechner law concerns a person’s sensed perception of various strengths of stimulation involving weights, sound, light, shock, taste, and so on. One form of the law states that the rate of change of sensed sen
> For a person learning to type, the number N of words per minute that the person could type after t hours of practice was given by the limited growth function N = 1001(1 - e-0.02t ) What is the rate of improvement after 10 hours of practice? After 40 ho
> Many countries have banned the use of the insecticide DDT because of its long-term adverse effects. Five years after a particular country stopped using DDT, the amount of DDT in the ecosystem had declined to 70% of the amount present at the time of the b
> A community of 10,000 people is homogeneously mixed. One person who has just returned from another community has influenza. Assume that the home community has not had influenza shots and all are susceptible. One mathematical model assumes that influenza
> Under certain assumptions, the blood pressure P in the largest artery in the human body (the aorta) changes between beats with respect to time t according to where a is a constant. Find P = P(t) that satisfies both conditions
> A company is trying to expose a new product to as many people as possible through online ads. Suppose that the rate of exposure to new people is proportional to the number of those who have not seen the product out of L possible viewers (limited growth).
> The marginal price dp/dx at x units of supply per day is proportional to the price p. There is no supply at a price of $20 per unit [p(0) = 20], and there is a daily supply of 40 units at a price of $23.47 per unit [p(40) = 23.47]. (A) Find the price–su
> Find the amount A in an account after t years if
> Find the amount A in an account after t years if
> Refer to Problem 75. Explain why the world population function Q(t) does not satisfy an exponential growth law. Data from Problem 75: Let Q(t) denote the population of the world at time t. In 1999, the world population was 6.0 billion and increasing at
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Find the value of t for which the logistic function is equal to M/2.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> use a graphing calculator to graph the given examples of the various cases in Table 1.
> Show that y = 2/ (1 + ce-6t) is a solution of the differential equation dy/dt = 3y(2 – y) for any real number c. Find the particular solution that passes through (0, 1).
> Show that y = C/x is a solution of the differential equation dy/dx = -y/x for any real number C. Find the particular solution that passes through (2, 5).
> Show that y = √x2 + C is a solution of the differential equation dy/dx = x/y for any real number C. Find the particular solution that passes through (-6, 7).
> Refer to the following slope fields: Use a graphing calculator to graph y = Cex - 1 for C = -2, -1, 1, and 2, for -5 ≤ x ≤ 5, -5 ≤ y ≤ 5, all in the same viewing window. Obse
> Refer to the following slope fields: Graph the particular solution found in Problem 54 in the appropriate Figure A or B (or a copy).
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Refer to the following slope fields: Show that y = Ce x- 1 is a solution of the differential equation dy/dx = y + 1 for any real number C. Find the particular solution that passes through (0, 0).
> Refer to the following slope fields: Which slope field is associated with the differential equation dy/dx = y + 1? Briefly justify your answer.
> does the given differential equation model unlimited growth, exponential decay, limited growth, or logistic growth? y(= 10,000 - y
> does the given differential equation model unlimited growth, exponential decay, limited growth, or logistic growth? y(= -0.0152y
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Find the general or particular solution, as indicated, for each differential equation.
> Refer to the following slope fields: Graph the particular solution found in Problem 36 in the appropriate Figure A or B (or a copy).
> Refer to the following slope fields: Solve the differential equation dy/dx = -x and find the particular solution that passes through (0, 3).
> Use the limiting matrix P found for each transition matrix P in Problems 29–34 to determine the long-run behavior of the successive state matrices for the indicated initial-state matrices
> Refer to the following slope fields: Which slope field is associated with the differential equation dy/dx = -x? Briefly justify your answer.
> Is y = e-3x a solution of the differential equation y( - 4y( + 3y = 0? Explain.
> Is y = -2ex a solution of the differential equation y’’ - 4y= + 3y = 0? Explain.
> Is y = 5ex2/2 a solution of the differential equation y’= xy? Explain.
> Give the order (first, second, third, etc.) of each differential equation, where y represents a function of the variable.
> Give the order (first, second, third, etc.) of each differential equation, where y represents a function of the variable.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> Find the general or particular solution, as indicated, for each first-order differential equation.
> find the limiting matrix for the indicated standard form. Find the long-run probability of going from each nonabsorbing state to each absorbing state and the average number of trials needed to go from each nonabsorbing state to an absorbing state.
> The function x(t) in Problem 95 exhibits logistic growth. Why might the rate at which a rumor spreads initially increase, but eventually slow down? Data from Problem 95:
> Find the general or particular solution, as indicated, for each first-order differential equation.
> A college language class was chosen for an experiment in learning. Using a list of 50 words, the experiment involved measuring the rate of vocabulary memorization at different times during a continuous 5-hour study session. It was found that the average
> Find the general or particular solution, as indicated, for each first-order differential equation.
> The area A of a healing wound changes at a rate given approximately by where t is time in days and A(1) = 2 square centimeters. What will the area of the wound be in 10 days?
> An average student enrolled in a steno typing class progressed at a rate of N′(t) = 12e-0.06t words per minute per week t weeks after enrolling in a 15-week course. If, at the beginning of the course, a student could stenotype at zero words per minute,
> If the rate of labor use in Problem 89 is L′(x) = 2,000x-1/3 and if the first 8 control units require 12,000 labor-hours, how many labor-hours, L(x), will be required for the first x control units? The first 27 control units?
> An oil tanker aground on a reef is losing oil and producing an oil slick that is radiating outward at a rate given approximately by where R is the radius (in feet) of the circular slick after t minutes. Find the radius of the slick after 16 minutes if
> Repeat Problem 86 if S′(t) = 500t1/4 + 300 and all other information remains the same. Use a graphing calculator to approximate the solution of the equation S(t)= 20,000 to two decimal places. Data from Problem 86: The rate of change of the monthly sale
> The rate of healing for a skin wound (in square centimeters per day) is approximated by A′(t) = -0.9e-0.1t If the initial wound has an area of 7 square centimeters, what will its area A(t) be after t days? After 5 days?
> find the limiting matrix for the indicated standard form. Find the long-run probability of going from each nonabsorbing state to each absorbing state and the average number of trials needed to go from each nonabsorbing state to an absorbing state.
> The rate of change of the monthly sales of a newly released football game is given by S′(t) = 500t 1/4 S(0) = 0 where t is the number of months since the game was released and S(t) is the number of games sold each month. Find S(t). When will monthly
> Assume that the rate in Problem 83 is found to be (A) When is the rate of production greatest? (B) How many barrels of oil Q1t2 will the field produce in the first t years if Q102 = 0? How many barrels will be produced in the first 5 years? (C) How l
> The graph of the marginal revenue function from the sale of x smart watches is given in the figure. (A) Using the graph shown, describe the shape of the graph of the revenue function R(x) as x increases from 0 to 1,000. (B) Find the equation of the marg
> Repeat Problem 81 if the monthly rate of increase in sales is found to be approximated by S′(t) = 20 - 20e-0.05t 0 ≤ t ≤ 24 Data from Problem 81: (A) What will be the total sales S1t2 t months after the beginning of the national campaign if we assume
> In 2016, U.S. consumption of renewable energy was 9.97 quadrillion Btu (or 9.97 * 1015 Btu). Since the 1950s, consumption has been growing at a rate (in quadrillion Btu per year) given by ′(t) = 0.002t + 0.03 where t is years after 1950. Find (t) and
> The weekly marginal revenue from the sale of x pairs of tennis shoes is given by where R(x) is revenue in dollars. Find the revenue function. Find the revenue from the sale of 1,000 pairs of shoes.
> Show that the indefinite integral of the difference of two functions is the difference of the indefinite integrals.
> The marginal price at a supply level of x bottles of laundry detergent per week is given by Find the price–supply equation if the distributor of the detergent is willing to supply 75 bottles a week at a price of $5.00 per bottle. How m
> Assuming that x [Hint: Use the chain rule after noting that ln |x| = ln ( -x) for x 6 0.]
> Find the family of all antiderivatives of each derivative.
> find the limiting matrix for the indicated standard form. Find the long-run probability of going from each nonabsorbing state to each absorbing state and the average number of trials needed to go from each nonabsorbing state to an absorbing state.
> Use differentiation to justify the formula
> Find the family of all antiderivatives of each derivative.
> find the derivative or indefinite integral as indicated.
> Find the family of all antiderivatives of each derivative.
> find the derivative or indefinite integral as indicated.
> Find each indefinite integral and check the result by differentiating.
> find each indefinite integral
> Find each indefinite integral and check the result by differentiating.
> find each indefinite integral
> Find each indefinite integral and check the result by differentiating.
> find a standard form for the absorbing Markov chain with the indicated transition matrix.
> identify the absorbing states for each transition diagram, and determine whether or not the diagram represents an absorbing Markov chain.
> You want to lift a heavy box with a mass of 98.0 kg using the two- ideal-pulley system as shown. With what minimum force do you have to pull down on the rope in order to lift the box at a constant velocity? One pulley is attached to the ceiling and one t
> A boy has stacked two blocks on the floor so that a 5.00 kg block is on top of a 2.00 kg block. (a) If the coefficient of static friction between the two blocks is 0.400 and the coefficient of static friction between the bottom block and the floor is 0.
> (a) If a spacecraft moves in a straight line between Earth and the Sun, at what point would the force of gravity on the spacecraft due to the Sun be as large as that due to Earth? (b) If the spacecraft is close to, but not at, this equilibrium point, do
> A student's head is bent over her physics book. The head weighs 50.0 N and is supported by the muscle force //
> A large wrecking ball of mass m is resting against a wall. It hangs from the end of a cable that is attached at its upper end to a crane that is just touching the wall. The cable makes an angle of θ with the wall. Ignoring friction between t
> Two canal workers pull a barge along the narrow waterway at a constant speed. One worker pulls with a force of 105 N at an angle of 28° with respect to the forward motion of the barge, and the other worker, on the opposite tow path, pulls at an angle of
> By what percentage does the weight of an object change when it is moved from the equator at sea level, where the effective value of g is 9.784 N/kg, to the North Pole where g = 9.832 N/kg?
> The tallest spot on Earth is Mt. Everest, which is 8850 m above sea level. If the radius of Earth to sea level is 6370 km, how much does the gravitational field strength change between the sea level value at that location (9.826 N/kg) and the top of Mt.
> Spring scale A is attached to the ceiling. A 10.0 kg object is suspended from the scale. A second spring scale, B, is hanging from a hook at the bottom of the 10.0 kg object and a 4.0 kg object hangs from the second spring scale. (a) What are the readin
> A 50.0 kg crate is suspended between the floor and the ceiling using two spring scales, one attached to the ceiling and one to the floor. If the lower scale reads 120 N, what is the reading of the upper scale? Ignore the weights of the scales.
> Rank vectors /