Question: A direction field for the differential equation
A direction field for the differential equation y' = tan (1/2 πy) is shown.
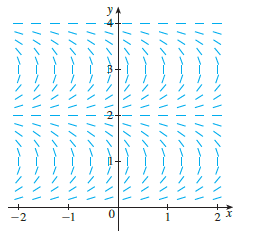
(a). Sketch the graphs of the solutions that satisfy the given initial conditions.
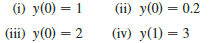
(b). Find all the equilibrium solutions.
Transcribed Image Text:
-1 ノーー \| らす///ーGー\\|*///ーロ \||| |I//レー\||///--~\\| -T |//レーーー\\|///-\| 「//レー\\|||//ー\\|+ () у(0) — 1 (ij) у(0) — 0.2 (iii) y(0) = 2 (iv) у(1) — 3
> A population of protozoa develops with a constant relative growth rate of 0.7944 per member per day. On day zero the population consists of two members. Find the population size after six days.
> The half-life of cesium-137 is 30 years. Suppose we have a 100-mg sample. (a). Find the mass that remains after years. (b). How much of the sample remains after 100 years? (c). After how long will only 1 mg remain?
> For which positive integers is the following series convergent? ∑∞n=1 (n!)2/(kn)!
> Strontium-90 has a half-life of 28 days. (a). A sample has a mass of 50 mg initially. Find a formula for the mass remaining after days. (b). Find the mass remaining after 40 days. (c). How long does it take the sample to decay to a mass of 2 mg? (d). Sk
> Experiments show that if the chemical reaction N2O5 → 2NO2 + 1/2O2 takes place at 450C, the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows: (a). Find an expression for the concentration [N2O5
> Solve the differential equation. (y + sin y) y' = x + x3
> A bacteria culture grows with constant relative growth rate. The bacteria count was 400 after 2 hours and 25,600 after 6 hours. (a). What is the relative growth rate? Express your answer as a percentage. (b). What was the intitial size of the culture? (c
> A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 420. (a). Find an expression for the number of bacteria after hours. (b). Find the number of bacteria after 3 hour
> Scientists can determine the age of ancient objects by the method of radiocarbon dating. The bombardment of the upper atmosphere by cosmic rays converts nitrogen to a radioactive isotope of carbon, 14C, with a half-life of about 5730 years. Vegetation ab
> A sample of tritium-3 decayed to 94.5% of its original amount after a year. (a). What is the half-life of tritium-3? (b). How long would it take the sample to decay to 20% of its original amount?
> Solve the differential equation. du/dt = 2 + 2u + t + tu
> Solve the differential equation. dy/dx = ey sin2θ/y sec θ
> Solve the differential equation. dy/dt = tet/y √1 + y2
> Let limn→∞ n√|an| = L The Root Test says the following: (i). If L (ii). If l > 1 (or L = ∞), then ∑an is divergent. (iii). If L = 1, then the Root Test is inconc
> Solve the differential equation. (y2 + xy2) y' = 1
> Solve the differential equation. (x2 + 1) y' = xy
> Solve the differential equation by making xy' = y + xey/x the change of variable v = y/x.
> Solve the differential equation y' = x + y by making the change of variable u =x + y.
> Find the function f such that f'(x) = f (x) (1 – f (x)) and f (0) = 1/2.
> Solve the differential equation. dy/dx = xe-y
> Find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is xy.
> Find the solution of the differential equation that satisfies the given initial condition. dL = = -1 kL² In t, L(1) dt
> Find the solution of the differential equation that satisfies the given initial condition. y' tan x 3D а + у, у(п/3) — а, 0<x<п/2
> Find the solution of the differential equation that satisfies the given initial condition. dP VPt, P(1) = 2 dt %3D
> Let limn→∞ n√|an| = L The Root Test says the following: (i). If L (ii). If l > 1 (or L = ∞), then ∑an is divergent. (iii). If L = 1, then the Root Test is inconc
> Find the solution of the differential equation that satisfies the given initial condition. x In x = y(1 + 3 + y? )y', y(1) = 1
> Find the solution of the differential equation that satisfies the given initial condition. du 2t + sec?t u(0) = -5 dt 2u
> Find the solution of the differential equation that satisfies the given initial condition. dy In x y(1) = 2 dx ху
> Find the solution of the differential equation that satisfies the given initial condition. dy dx y(0) = -3 y ||
> Solve the differential equation. dz/dx + et+z = 0
> Solve the differential equation. dy/dx = xy2
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = 1/2 y
> Use the direction field labeled IV (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — — 1 (b) у(0) — 0 (с) у(0) — 1 %3D %3D
> Use the direction field labeled II (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — 1 (b) у(0) — 2 (с) у(0) — —1 %3!
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = sin x sin y II y4 у. IV y4 -- III -- + 2 X -2
> For which of the following series is the Ratio Test inconclusive (that is, it fails to give a definite answer)? (a) (b) (-3)ª-1 ( d) Σ -i 1 + n? - |
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x + y - 1 II y4 у. IV y4 -- III -- + 2 X -2
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x (2 - y) II y4 у. IV y4 -- III -- + 2 X -2
> A population is modeled by the differential equation dP/dt = 1.2P (1 – P/4200) (a). For what values of P is the population increasing? (b). For what values of P is the population decreasing? (c). What are the equilibrium solutions?
> (a). Show that every member of the family of functions y = (ln x + C)/x is a solution of the differential equation x2y' + xy = 1. (b). Illustrate part (a) by graphing several members of the family of solutions on a common screen. (c). Find a solution of
> Which of the following functions are solutions of the differential equation y" + y = sin x? (a) y = sin x (b) y = cosx (c) y = }x sin x (d) y = -x cos x
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. II y4 у. IV y4 -- III -- + 2 X -2 y' = 2 – y
> (a). For what values of does the function y = cos kt satisfy the differential equation 4y" = -25? (b). For those values of k, verify that every member of the family of functions y = A sin kt + B cos kt is also a solution.
> The figure shows a circuit containing an electromotive force, a capacitor with a capacitance of C farads (F), and a resistor with a resistance of R ohms (Ω). The voltage drop across the capacitor is Q/C, where Q is the charge (in coul
> Use Euler’s method with step size 0.1 to estimate y (0.5), where y (x) is the solution of the initial-value problem y' = y + xy, y (0) = 1.
> Use Euler’s method with step size 0.2 to estimate y (1), where y (x) is the solution of the initial-value problem y' = xy – x2, y (0) = 1.
> Let p and q be real numbers with p (а) (р, q) (с) [р. 9) (b) (р, q] (d) [р, q]
> Use Euler’s method with step size 0.5 to compute the approximate y-values y1, y2, y3 and y4 of the solution of the initial-value problem y' = y – 2x, y (1) = 0.
> A direction field for a differential equation is shown. Draw, with a ruler, the graphs of the Euler approximations to the solution curve that passes through the origin. Use step sizes h = 1 and h = 0.5. Will the Euler estimates be under - estimates or ov
> (a). Use Euler’s method with each of the following step sizes to estimate the value of y (0.4), where is the solution of the initial-value problem y' = y, y (0) = 1. (b). We know that the exact solution of the initial-value problem in
> (a). For what values of does the function y = erx satisfy the differential equation 2y" + y' – y = 0? (b). If r1 and r2 are the values of r that you found in part (a), show that every member of the family of functions y = aer1x + ber2x is also a solution
> Use a computer algebra system to draw a direction field for the differential equation y' = y3 – 4y. Get a printout and sketch on its solutions that satisfy the initial condition y (0) = c for various values of c. For what values of c does limx→∞ y (t) ex
> Verify that y = -t cos t – t is a solution of the initial-value problem dy d =y +t°sin t y(7) = 0
> According to Newton’s Law of Universal Gravitation, the gravitational force on an object of mass m that has been projected vertically upward from the earth’s surface is Where x = x (t) is the objectâ€
> Let A (t) be the area of a tissue culture at time t and let M be the final area of the tissue when growth is complete. Most cell divisions occur on the periphery of the tissue and the number of cells on the periphery is proportional to √A (t). So, a reas
> Homeostasis refers to a state in which the nutrient content of a consumer is independent of the nutrient content of its food. In the absence of homeostasis, a model proposed by Sterner and Elser is given by where and represent the nutrient content of t
> Let x = 0.99999… (a). Do you think that x < 1 or x = 4? (b). Sum a geometric series to find the value of x. (c). How many decimal representations does the number 1 have? (d). Which numbers have more than one decimal representation?
> Find the radius of convergence and interval of convergence of the series. 10"x" Σ 00 A-1
> Allometric growth in biology refers to relationships between sizes of parts of an organism (skull length and body length, for instance). If L1 (t) and L2 (t) are the sizes of two organs in an organism of age t, then L1 and L2 satisfy an allometric law if
> An object of mass m is moving horizontally through a medium which resists the motion with a force that is a function of the velocity; that is, Where v = v (t) and s = s (t) represents the velocity and position of the object at time t, respectively. Fo
> When a raindrop falls, it increases in size and so its mass at time t is a function of t, namely m (t). The rate of growth of the mass is km (t) for some positive constant k. When we apply New ton’s Law of Motion to the raindrop, we get (mv)' = gm, where
> A tank contains 1000 L of pure water. Brine that contains 0.05 kg of salt per liter of water enters the tank at a rate of 5 L/min. Brine that contains 0.04 kg of salt per liter of water enters the tank at a rate of 10 L/min. The solution is kept thorough
> A vat with 500 gallons of beer contains 4% alcohol (by volume). Beer with 6% alcohol is pumped into the vat at a rate of 5 gal/min and the mixture is pumped out at the same rate. What is the percentage of alcohol after an hour?
> The air in a room with volume 180m3 contains 0.15% carbon dioxide initially. Fresher air with only 0.05% carbon dioxide flows into the room at a rate of 2 m3/min and the mixed air flows out at the same rate. Find the percentage of carbon dioxide in the r
> A tank contains 1000 L of brine with 15 kg of dissolved salt. Pure water enters the tank at a rate of 10 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank (a) after minutes and (b) after
> A certain small country has $10 billion in paper currency in circulation, and each day $50 million comes into the country’s banks. The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency
> A glucose solution is administered intravenously into the bloodstream at a constant rate r. As the glucose is added, it is converted into other substances and removed from the bloodstream at a rate that is proportional to the concentration at that time.
> For a fixed value of M (say M = 10), the family of logistic functions given by Equation 4 depends on the initial value P0 and the proportionality constant k. Graph several members of this family. How does the graph change when P0 varies? How does it chan
> Suppose that the radius of convergence of the power series ∑cnxn is R. What is the radius of convergence of the power series ∑cnx2n?
> Explain why the functions with the given graphs can’t be solutions of the differential equation dy = e'(y – 1)? dt (а) у (b) у. 1+ 1+ 1
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = x – y + 1
> The table gives the number of yeast cells in a new labora tory culture. (a). Plot the data and use the plot to estimate the carrying capacity for the yeast population. (b). Use the data to estimate the initial relative growth rate. (c). Find both an ex
> The table gives estimates of the world population, in millions, from 1750 to 2000. (a). Use the exponential model and the population figures for 1750 and 1800 to predict the world population in 1900 and 1950. Compare with the actual figures. (b). Use t
> Suppose that a population grows according to a logistic model with carrying capacity 6000 and k = 0.0015 per year. (a). Write the logistic differential equation for these data. (b). Draw a direction field (either by hand or with a com puter algebra syste
> Suppose that a population develops according to the logistic equation dP/dt = 0.05P – 0.0005P2 where t is measured in weeks. (a). What is the carrying capacity? What is the value of k? (b). A direction field for this equation is shown.
> Suppose you have just poured a cup of freshly brewed coffee with temperature 950C in a room where the temperature is 200C. (a). When do you think the coffee cools most quickly? What happens to the rate of cooling as time goes by? Explain. (b). Newton’s L
> Make a rough sketch of a direction field for the autonomous differential equation y' = f (y), where the graph of f is as shown. How does the limiting behavior of solutions depend on the value of y (0)? fy)A -2 -1 0 y
> Psychologists interested in learning theory study learning curves. A learning curve is the graph of a function P (t), the performance of someone learning a skill as a function of the training time t. The derivative dP/dt represents the rate at which perf
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y' =
> Suppose the series ∑cnxn has radius of convergence 2 and the series ∑dnxn has radius of convergence 3. What is the radius of convergence of the series ∑(cn + dn)?
> Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the solution curve and compare it with your sketch. y' =
> In a murder investigation, the temperature of the corpse was 32.50C at 1:30 PM and an hour later. Normal body temperature is 37.00C and the temperature of the surroundings was 20.00C. When did the murder take place?
> Sketch the direction field of the differential equation. Then use it to sketch a solution curve that passes through the given point. у — у+ ху, (0, 1)
> (a). Use a computer algebra system to draw a direction field for the differential equation. Get a printout and use it to sketch some solution curves without solving the differential equation. (b). Solve the differential equation. (c). Use the CAS to draw
> The function with the given graph is a solution of one of the following differential equations. Decide which is the correct equation and justify your answer. A. y' = 1+ xy B. y' = -2xy C. y' = 1 - 2xy
> Solve the equation y' = x √x2 + 1/ (y ey) and graph several members of the family of solutions (if your CAS does implicit plots). How does the solution curve change as the constant C varies?
> Solve the initial-value problem y' = (sin x)/ sin y, y (0) = π/2, and graph the solution (if your CAS does implicit plots).
> Solve the equation e-yy' + cos x = 0 and graph several members of the family of solutions. How does the solution curve change as the constant C varies?
> (a). What can you say about the graph of a solution of the equation y = xy3 when is close to 0? What if is large? (b). Verify that all members of the family y = (c – x2)-1/2 are solutions of the differential equation y' = xy3. (c). Graph several members
> (a). What can you say about a solution of the equation y' = -y2 just by looking at the differential equation? (b). Verify that all members of the family y = 1/ (x + C) are solutions of the equation in part (a). (c). Can you think of a solution of the dif
> If f (x) =∑∞n=0 cnxn, where cn+4 = cn for all n > 0, find the interval of convergence of the series and a formula for f (x).
> The table gives the population of India, in millions, for the second half of the 20th century. (a). Use the exponential model and the census figures for 1951 and 1961 to predict the population in 2001. Compare with the actual figure. (b). Use the expon
> Suppose we alter the differential equation in Exercise 19 as follows: Exercise 19: In a seasonal-growth model, a periodic function of time is introduced to account for seasonal variations in the rate of growth. Such variations could, for example, be c
> In a seasonal-growth model, a periodic function of time is introduced to account for seasonal variations in the rate of growth. Such variations could, for example, be caused by seasonal changes in the availability of food. (a). Find the solution of the s
> Another model for a growth function for a limited population is given by the Gompertz function, which is a solution of the differential equation where c is a constant and M is the carrying capacity. (a). Solve this differential equation. (b). Compute l
> There is considerable evidence to support the theory that for some species there is a minimum population m such that the species will become extinct if the size of the population falls below m. This condition can be incorporated into the logistic equatio
> Consider the differential equation as a model for a fish population, where is measured in weeks and c is a constant. (a). Use a CAS to draw direction fields for various values of c. (b). From your direction fields in part (a), determine the values of f
> Let’s modify the logistic differential equation of Example 1 as follows: (a). Suppose P (t) represents a fish population at time t, where is measured in weeks. Explain the meaning of the final term in the equation (-15). (b). Draw a d
> The table gives the midyear population of Spain, in thousands, from 1955 to 2000. Use a graphing calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy
> The table gives the midyear population of Japan, in thousands, from 1960 to 2005. Use a graphing calculator to fit both an exponential function and a logistic function to these data. Graph the data points and both functions, and comment on the accuracy

