Question: Find the solution of the differential equation
Find the solution of the differential equation that satisfies the given initial condition.
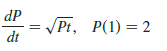
Transcribed Image Text:
dP VPt, P(1) = 2 dt %3D
> (a). Program a calculator or computer to use Euler’s method to compute y (1), where y (x) is the solution of the initial value problem (b). Verify that y = 2 + e-x3 is the exact solution of the differential equation. (c). Find the er
> (a). Use Euler’s method with step size 0.2 to estimate y (0.4), where y (x) is the solution of the initial-value problem y' = x + y2, y (0) = 0. (b). Repeat part (a) with step size 0.1.
> (a). Solve the differential equation y' = 2x√1 – y2. (b). Solve the initial-value problem y' = 2x√1 – y2, y (0) = 0, and graph the solution. (c). Does the initial-value problem y' = 2x√1 – y2, y (0) = 2, have a solution? Explain.
> Let c be a positive number. A differential equation of the form dy/dt = ky1+c where is a positive constant, is called a doomsday equation because the exponent in the expression is larger than the exponent 1 for natural growth. (a). Determine the solution
> Consider a population P = P (t) with constant relative birth and death rates α and β, respectively, and a constant emigration rate m, where α, β, and m are positive constants. Assume that α
> (a). How long will it take an investment to double in value if the interest rate is 6% compounded continuously? (b). What is the equivalent annual interest rate?
> Around 1910, the Indian mathematician Srinivasa Ramanujan discovered the formula William Gosper used this series in 1985 to compute the first 17 million digits of π. (a). Verify that the series is convergent. (b). How many correct decimal pl
> (a). If $3000 is invested at 5% interest, find the value of the investment at the end of 5 years if the interest is compounded (i) annually, (ii) semiannually, (iii) monthly, (iv) weekly, (v) daily, and (vi) continuously. (b). If A (T) is the amount of t
> (a). If $1000 is borrowed at 8% interest, find the amounts due at the end of 3 years if the interest is compounded (i) annually, (ii) quarterly, (iii) monthly, (iv) weekly, (v) daily, (vi) hourly, and (vii) continuously. (b). Suppose $1000 is borrowed an
> The rate of change of atmospheric pressure P with respect to altitude h is proportional to P, provided that the temperature is constant. At 150C the pressure is 101.3kPa at sea level and 87.14 kPa at h = 1000m. (a). What is the pressure at an altitude of
> A freshly brewed cup of coffee has temperature 950C in a 200C room. When its temperature is 700C, it is cooling at a rate of 10C per minute. When does this occur?
> When a cold drink is taken from a refrigerator, its temperature is 50C. After 25 minutes in a 200C room its temperature has increased to 100C. (a). What is the temperature of the drink after 50 minutes? (b). When will its temperature be 150C?
> Find the solution of the differential equation that satisfies the given initial condition. xy sin x y' y +1 y(0) = 1 '
> A roast turkey is taken from an oven when its temperature has reached 1850F and is placed on a table in a room where the temperature is 750F. (a). If the temperature of the turkey is 1500F after half an hour, what is the temperature after 45 minutes? (b
> A curve passes through the point (0, 5) and has the property that the slope of the curve at every point P is twice the y-coordinate of P. What is the equation of the curve?
> (a). Show that if P satisfies the logistic equation (1), then d2P/dt2 = k2P (1 – P/M) (1 – 2P/M). (b). Deduce that a population grows fastest when it reaches half its carrying capacity.
> Biologists stocked a lake with 400 fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 10,000. The number of fish tripled in the first year. (a). Assuming that the size of the fish population
> (a). Show that ∑∞n=0 xn/n! converges for all x. (b). Deduce that limn→∞ xn/n! = 0 for all x.
> In Example 1(b) we showed that the rabbit and wolf populations satisfy the differential equation By solving this separable differential equation, show that where C is a constant. It is impossible to solve this equation for W, as an explicit function
> Graphs of populations of two species are shown. Use them to sketch the corresponding phase trajectory. y species 1 1200- 1000 800 600 400 species 2 200 5 10 15
> Graphs of populations of two species are shown. Use them to sketch the corresponding phase trajectory. y. species 1 200+ species 2 150+ 100+ 50 1
> Solve the differential equation. du/dr = 1 + √r/1 + √u
> Suppose a population grows according to a logistic model with initial population 1000 and carrying capacity 10,000. If the population grows to 2500 after one year, what will the population be after another three years?
> Suppose a population P (t) satisfies dP/dt = 0.4P – 0.001P2, P (0) = 50 where t is measured in years. (a). What is the carrying capacity? (b). What is P'(0)? (c). When will the population reach 50% of the carrying capacity?
> The Pacific halibut fishery has been modeled by the differential equation where y (t) is the biomass (the total mass of the members of the population) in kilograms at time t (measured in years), the carrying capacity is estimated to be M = 8 Ã&#
> A common inhabitant of human intestines is the bacterium Escherichia coli. A cell of this bacterium in a nutrient-broth medium divides into two cells every 20 minutes. The initial population of a culture is 60 cells. (a). Find the relative growth rate. (
> A population of protozoa develops with a constant relative growth rate of 0.7944 per member per day. On day zero the population consists of two members. Find the population size after six days.
> The half-life of cesium-137 is 30 years. Suppose we have a 100-mg sample. (a). Find the mass that remains after years. (b). How much of the sample remains after 100 years? (c). After how long will only 1 mg remain?
> For which positive integers is the following series convergent? ∑∞n=1 (n!)2/(kn)!
> Strontium-90 has a half-life of 28 days. (a). A sample has a mass of 50 mg initially. Find a formula for the mass remaining after days. (b). Find the mass remaining after 40 days. (c). How long does it take the sample to decay to a mass of 2 mg? (d). Sk
> Experiments show that if the chemical reaction N2O5 → 2NO2 + 1/2O2 takes place at 450C, the rate of reaction of dinitrogen pentoxide is proportional to its concentration as follows: (a). Find an expression for the concentration [N2O5
> Solve the differential equation. (y + sin y) y' = x + x3
> A bacteria culture grows with constant relative growth rate. The bacteria count was 400 after 2 hours and 25,600 after 6 hours. (a). What is the relative growth rate? Express your answer as a percentage. (b). What was the intitial size of the culture? (c
> A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 420. (a). Find an expression for the number of bacteria after hours. (b). Find the number of bacteria after 3 hour
> Scientists can determine the age of ancient objects by the method of radiocarbon dating. The bombardment of the upper atmosphere by cosmic rays converts nitrogen to a radioactive isotope of carbon, 14C, with a half-life of about 5730 years. Vegetation ab
> A sample of tritium-3 decayed to 94.5% of its original amount after a year. (a). What is the half-life of tritium-3? (b). How long would it take the sample to decay to 20% of its original amount?
> Solve the differential equation. du/dt = 2 + 2u + t + tu
> Solve the differential equation. dy/dx = ey sin2θ/y sec θ
> Solve the differential equation. dy/dt = tet/y √1 + y2
> Let limn→∞ n√|an| = L The Root Test says the following: (i). If L (ii). If l > 1 (or L = ∞), then ∑an is divergent. (iii). If L = 1, then the Root Test is inconc
> Solve the differential equation. (y2 + xy2) y' = 1
> Solve the differential equation. (x2 + 1) y' = xy
> Solve the differential equation by making xy' = y + xey/x the change of variable v = y/x.
> Solve the differential equation y' = x + y by making the change of variable u =x + y.
> Find the function f such that f'(x) = f (x) (1 – f (x)) and f (0) = 1/2.
> Solve the differential equation. dy/dx = xe-y
> Find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is xy.
> Find the solution of the differential equation that satisfies the given initial condition. dL = = -1 kL² In t, L(1) dt
> Find the solution of the differential equation that satisfies the given initial condition. y' tan x 3D а + у, у(п/3) — а, 0<x<п/2
> Let limn→∞ n√|an| = L The Root Test says the following: (i). If L (ii). If l > 1 (or L = ∞), then ∑an is divergent. (iii). If L = 1, then the Root Test is inconc
> Find the solution of the differential equation that satisfies the given initial condition. x In x = y(1 + 3 + y? )y', y(1) = 1
> Find the solution of the differential equation that satisfies the given initial condition. du 2t + sec?t u(0) = -5 dt 2u
> Find the solution of the differential equation that satisfies the given initial condition. dy In x y(1) = 2 dx ху
> Find the solution of the differential equation that satisfies the given initial condition. dy dx y(0) = -3 y ||
> Solve the differential equation. dz/dx + et+z = 0
> Solve the differential equation. dy/dx = xy2
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = 1/2 y
> Use the direction field labeled IV (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — — 1 (b) у(0) — 0 (с) у(0) — 1 %3D %3D
> Use the direction field labeled II (above) to sketch the graphs of the solutions that satisfy the given initial conditions. (а) у(0) — 1 (b) у(0) — 2 (с) у(0) — —1 %3!
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = sin x sin y II y4 у. IV y4 -- III -- + 2 X -2
> For which of the following series is the Ratio Test inconclusive (that is, it fails to give a definite answer)? (a) (b) (-3)ª-1 ( d) Σ -i 1 + n? - |
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x + y - 1 II y4 у. IV y4 -- III -- + 2 X -2
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. y' = x (2 - y) II y4 у. IV y4 -- III -- + 2 X -2
> A population is modeled by the differential equation dP/dt = 1.2P (1 – P/4200) (a). For what values of P is the population increasing? (b). For what values of P is the population decreasing? (c). What are the equilibrium solutions?
> (a). Show that every member of the family of functions y = (ln x + C)/x is a solution of the differential equation x2y' + xy = 1. (b). Illustrate part (a) by graphing several members of the family of solutions on a common screen. (c). Find a solution of
> Which of the following functions are solutions of the differential equation y" + y = sin x? (a) y = sin x (b) y = cosx (c) y = }x sin x (d) y = -x cos x
> Match the differential equation with its direction field (labeled I–IV). Give reasons for your answer. II y4 у. IV y4 -- III -- + 2 X -2 y' = 2 – y
> (a). For what values of does the function y = cos kt satisfy the differential equation 4y" = -25? (b). For those values of k, verify that every member of the family of functions y = A sin kt + B cos kt is also a solution.
> The figure shows a circuit containing an electromotive force, a capacitor with a capacitance of C farads (F), and a resistor with a resistance of R ohms (Ω). The voltage drop across the capacitor is Q/C, where Q is the charge (in coul
> Use Euler’s method with step size 0.1 to estimate y (0.5), where y (x) is the solution of the initial-value problem y' = y + xy, y (0) = 1.
> Use Euler’s method with step size 0.2 to estimate y (1), where y (x) is the solution of the initial-value problem y' = xy – x2, y (0) = 1.
> Let p and q be real numbers with p (а) (р, q) (с) [р. 9) (b) (р, q] (d) [р, q]
> Use Euler’s method with step size 0.5 to compute the approximate y-values y1, y2, y3 and y4 of the solution of the initial-value problem y' = y – 2x, y (1) = 0.
> A direction field for a differential equation is shown. Draw, with a ruler, the graphs of the Euler approximations to the solution curve that passes through the origin. Use step sizes h = 1 and h = 0.5. Will the Euler estimates be under - estimates or ov
> A direction field for the differential equation y' = tan (1/2 Ï€y) is shown. (a). Sketch the graphs of the solutions that satisfy the given initial conditions. (b). Find all the equilibrium solutions. -1 ノーー \| らす///ーGー\\|*///ーロ \||| |I
> (a). Use Euler’s method with each of the following step sizes to estimate the value of y (0.4), where is the solution of the initial-value problem y' = y, y (0) = 1. (b). We know that the exact solution of the initial-value problem in
> (a). For what values of does the function y = erx satisfy the differential equation 2y" + y' – y = 0? (b). If r1 and r2 are the values of r that you found in part (a), show that every member of the family of functions y = aer1x + ber2x is also a solution
> Use a computer algebra system to draw a direction field for the differential equation y' = y3 – 4y. Get a printout and sketch on its solutions that satisfy the initial condition y (0) = c for various values of c. For what values of c does limx→∞ y (t) ex
> Verify that y = -t cos t – t is a solution of the initial-value problem dy d =y +t°sin t y(7) = 0
> According to Newton’s Law of Universal Gravitation, the gravitational force on an object of mass m that has been projected vertically upward from the earth’s surface is Where x = x (t) is the objectâ€
> Let A (t) be the area of a tissue culture at time t and let M be the final area of the tissue when growth is complete. Most cell divisions occur on the periphery of the tissue and the number of cells on the periphery is proportional to √A (t). So, a reas
> Homeostasis refers to a state in which the nutrient content of a consumer is independent of the nutrient content of its food. In the absence of homeostasis, a model proposed by Sterner and Elser is given by where and represent the nutrient content of t
> Let x = 0.99999… (a). Do you think that x < 1 or x = 4? (b). Sum a geometric series to find the value of x. (c). How many decimal representations does the number 1 have? (d). Which numbers have more than one decimal representation?
> Find the radius of convergence and interval of convergence of the series. 10"x" Σ 00 A-1
> Allometric growth in biology refers to relationships between sizes of parts of an organism (skull length and body length, for instance). If L1 (t) and L2 (t) are the sizes of two organs in an organism of age t, then L1 and L2 satisfy an allometric law if
> An object of mass m is moving horizontally through a medium which resists the motion with a force that is a function of the velocity; that is, Where v = v (t) and s = s (t) represents the velocity and position of the object at time t, respectively. Fo
> When a raindrop falls, it increases in size and so its mass at time t is a function of t, namely m (t). The rate of growth of the mass is km (t) for some positive constant k. When we apply New ton’s Law of Motion to the raindrop, we get (mv)' = gm, where
> A tank contains 1000 L of pure water. Brine that contains 0.05 kg of salt per liter of water enters the tank at a rate of 5 L/min. Brine that contains 0.04 kg of salt per liter of water enters the tank at a rate of 10 L/min. The solution is kept thorough
> A vat with 500 gallons of beer contains 4% alcohol (by volume). Beer with 6% alcohol is pumped into the vat at a rate of 5 gal/min and the mixture is pumped out at the same rate. What is the percentage of alcohol after an hour?
> The air in a room with volume 180m3 contains 0.15% carbon dioxide initially. Fresher air with only 0.05% carbon dioxide flows into the room at a rate of 2 m3/min and the mixed air flows out at the same rate. Find the percentage of carbon dioxide in the r
> A tank contains 1000 L of brine with 15 kg of dissolved salt. Pure water enters the tank at a rate of 10 L/min. The solution is kept thoroughly mixed and drains from the tank at the same rate. How much salt is in the tank (a) after minutes and (b) after
> A certain small country has $10 billion in paper currency in circulation, and each day $50 million comes into the country’s banks. The government decides to introduce new currency by having the banks replace old bills with new ones whenever old currency
> A glucose solution is administered intravenously into the bloodstream at a constant rate r. As the glucose is added, it is converted into other substances and removed from the bloodstream at a rate that is proportional to the concentration at that time.
> For a fixed value of M (say M = 10), the family of logistic functions given by Equation 4 depends on the initial value P0 and the proportionality constant k. Graph several members of this family. How does the graph change when P0 varies? How does it chan
> Suppose that the radius of convergence of the power series ∑cnxn is R. What is the radius of convergence of the power series ∑cnx2n?
> Explain why the functions with the given graphs can’t be solutions of the differential equation dy = e'(y – 1)? dt (а) у (b) у. 1+ 1+ 1
> Sketch a direction field for the differential equation. Then use it to sketch three solution curves. y' = x – y + 1
> The table gives the number of yeast cells in a new labora tory culture. (a). Plot the data and use the plot to estimate the carrying capacity for the yeast population. (b). Use the data to estimate the initial relative growth rate. (c). Find both an ex
> The table gives estimates of the world population, in millions, from 1750 to 2000. (a). Use the exponential model and the population figures for 1750 and 1800 to predict the world population in 1900 and 1950. Compare with the actual figures. (b). Use t
> Suppose that a population grows according to a logistic model with carrying capacity 6000 and k = 0.0015 per year. (a). Write the logistic differential equation for these data. (b). Draw a direction field (either by hand or with a com puter algebra syste

