Question:
(a). Eliminate the parameter to find a Cartesian equation of the curve.
(b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases.
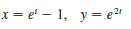
Transcribed Image Text:
x = e' – 1, y = e2"
> If a bacteria population starts with 100 bacteria and doubles every three hours, then the number of bacteria after hours is n – f (t) = 100 ∙ 2t/3. (a). Find the inverse of this function and explain its meaning. (b). When will the population reach 50,00
> Find the exponential function f (x) = Cax whose graph is given. y4 (3, 24), (1, 6)
> Find the domain of each function. (a). g (t) = sin (e-t) (b). g (t) = √1 - 2t
> Find (a) the domain of f and (b) f-1 and its domain. f (x) = ln (2 + ln x)
> Find (a) the domain of f and (b) f-1 and its domain. f (x) = √3 - e2x
> Solve each inequality for x. (a). 2 < ln x < 9 (b). e2-3x > 4
> Solve each inequality for x. (a). ex > 10 (b). ln x > -1
> Solve each equation for x. (a). ln (ln x) = 1 (b). eax = Cebx, where a ≠ b
> Solve each equation for x. (a). 2x-5 = 3 (b). ln x + ln (x – 1) = 1
> Solve each equation for x. (a). ln (x2 – 1) = 3 (b). e2x – 3ex + 2 = 0
> Match the graphs of the parametric equations x = f (t) and y = g (t) in (a)–(d) with the parametric curves labeled I–IV. Give reasons for your choices. (a) I YA 2+ 1- 1 1 II 2. + III 2 t (d) IV 2+ 2 t 2 х
> Solve each equation for x. (a). e7-4x = 6 (b). ln (3x -10) = 2
> Use the Law of Exponents to rewrite and simplify the expression. (a). 84/3 (b). x (3x2)3
> Find the domain of each function. (a). f (x) = 1 – ex2 /1 – e1-x2 (b). f (x) = 1 + x/e cos x
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = e |x| y4 10 4" 1.5 1 y y = e* m=1
> Suppose that the graph of y = log2x is drawn on a coordinate grid where the unit of measurement is an inch. How many miles to the right of the origin do we have to move before the height of the curve reaches ft?
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = -2-x y4 10 4" 1.5 1 y y = e* m=1
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = (0.5) x - 2 y4 10 4" 1.5 1 y y = e* m=1
> Use Formula 10 to evaluate each logarithm correct to six decimal places. (a). log12 10 (b). log2 8.4
> Express the given quantity as a single logarithm. ln (1 + x2) + 1/2 ln x - ln sin x
> Express the given quantity as a single logarithm. ln (a + b) + ln (a – b) - 2 ln c
> Starting with the graph of y = ex, write the equation of the graph that results from (a). shifting 2 units downward (b). shifting 2 units to the right (c). reflecting about the x-axis (d). reflecting about the y-axis (e). reflecting about the x-axis and
> Express the given quantity as a single logarithm. ln 5 + 5 ln 3
> Find the exact value of each expression. (a). e-2ln 5 (b). ln (ln ee10)
> Derive Equations 1 for the case π/2 < θ < π.
> Find the exact value of each expression. (a). ln (1/e) (b). log10 √10
> Find the exact value of each expression. (a). log5 125 (b). log3 (1/27)
> (a). What is the natural logarithm? (b). What is the common logarithm? (c). Sketch the graphs of the natural logarithm function and the natural exponential function with a common set of axes.
> (a). How is the logarithmic function y = logax defined? (b). What is the domain of this function? (c). What is the range of this function? (d). Sketch the general shape of the graph of the function if y = logax a > 1.
> (a). Find parametric equations for the ellipse x2/a2 + y2/b2 = 1. [Hint: Modify the equations of the circle in Example 2.] (b). Use these parametric equations to graph the ellipse when a = 3 and b = 1, 2, 4, and 8. (c). How does the shape of the ellipse
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = 10x+2 y4 10 4" 1.5 1 y y = e* m=1
> Use the given graph of f to sketch the graph of f-1. yA 1 2
> Describe the motion of a particle with position (x, y) as varies in the given interval. x= sin t, y = cos't, , -27sts 2m
> Use the given graph of f to sketch the graph of f-1. -1 1/
> Find an explicit formula for f-1 and use it to graph f-1, f and the line y = x on the same screen. To check your work, see whether the graphs of f and f-1 are reflections about the line. f (x) = 2 - ex
> Graph the curve x = y – 2sin πy.
> Find a formula for the inverse of the function. y = ex/1 + 2ex
> Find a formula for the inverse of the function. y = ln (x + 3)
> Find a formula for the inverse of the function. y = x2 – x, x > 1/2
> Find a formula for the inverse of the function. f (x) = e2x-1
> Find a formula for the inverse of the function. f (x) = 4x – 1/2x + 3
> Suppose a curve is given by the parametric equations x = f (t), y = g (t), where the range of f is [1,4] and the range of g is [2, 3]. What can you say about the curve?
> In the theory of relativity, the mass of a particle with speed v is where m0 is the rest mass of the particle and is the speed of light in a vacuum. Find the inverse function of f and explain its meaning. mo m = f(u) = VI - v/c²
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = 2 (1 – ex) y4 10 4" 1.5
> Describe the motion of a particle with position (x, y) as varies in the given interval. x = 5 sin t, y = 2 cos t, -TsI< 57
> Describe the motion of a particle with position (x, y) as varies in the given interval. x= 2 sin t, y = 4 + cos t, 0st<37/2
> If g (x) = 3 + x + ex, find g-1(4).
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x= In t, y = Vī,
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x= sin 0, y = cos 20
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x = e", y =t + 1
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. g (x) = cos x
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x= sin t, y = csc t, 0<t<T/2
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x = cos 0, y = 2 sin 0, 0< 0 <
> The graph of f is given. (a). Why is f one-to-one? (b). What are the domain and range of f-1? (c). What is the value of f-1 (2)? (d). Estimate the value of f-1 (0). 이 1
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x= sin 0, y = cos- 30,
> (a). Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. (b). Eliminate the parameter to find a Cartesian equation of the curve. x= t?, y =t
> (a). Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. (b). Eliminate the parameter to find a Cartesian equation of the curve. x= Vf, y=1 - t
> (a). Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. (b). Eliminate the parameter to find a Cartesian equation of the curve. x=1+ 3t, y= 2 – t?
> If the circle C rolls on the outside of the fixed circle, the curve traced out by P is called an epicycloid. Find parametric equations for the epicycloid.
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as increases. x= e + t, y = et – t, -2 < t<2
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as increases. x = cos't, y = 1 – sin t, 0 <ts 7/2 %3D
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as increases. x = t?, y=t - 4t, -3 <t<3
> A hypocycloid is a curve traced out by a fixed point P on a circle C of radius b as C rolls on the inside of a circle with center O and radius a. Show that if the initial position of P is (a, 0) and the parameter θ is chosen as in the figure
> Draw the graph of the equation x4 – 4x2 – x2y2 + 4y2 = 0.
> Describe the motion of a particle with position (x, y) as varies in the given interval. x = 3 + 2 cos t, y=1 + 2 sin t, /2 <t< 3m/2
> Sketch the graph of the function g (x) = |x2 – 1| - |x2 – 4|.
> Sketch the graph of the function f (x) = |x2 – 4| x| + 3|.
> The altitude perpendicular to the hypotenuse of a right triangle is 12 cm. Express the length of the hypotenuse as a function of the perimeter.
> If f0 (x) = x2 and fn+1 (x) = f0 (fn (x)) for n = 0, 1, 2, …, find a formula for fn (x).
> Solve the inequality ln (x2 – 2x - 2) < 0.
> (a). Show that the function f (x) = ln (x + √x2 + 1) is an odd function. (b). Find the inverse function of f.
> Evaluate (log23) (log34) (log45) …(log3132).
> One of the legs of a right triangle has length 4 cm. Express the length of the altitude perpendicular to the hypotenuse as a function of the length of the hypotenuse.
> Find the domain and range of the function. Write your answer in interval notation. F (t) = 3 + cos 2t
> Find the domain and range of the function. Write your answer in interval notation. h (x) = ln (x + 6)
> If f (x) = x5 + x3 + x, find f-1 (3) and f (f-1(2)).
> Find the domain and range of the function. Write your answer in interval notation. g (x) = √16 – x2
> Find the domain and range of the function. Write your answer in interval notation. f (x) = 2/ (3x – 1)
> Sketch a rough graph of the yield of a crop as a function of the amount of fertilizer used.
> Use parametric equations to graph the function f (x) = 2x + ln x and its inverse function on the same screen.
> (a). Sketch the curve represented by the parametric equations x = et, y = √t, 0 < t < 1, and indicate with an arrow the direction in which the curve is traced as increases. (b). Eliminate the parameter to find a Cartesian equation of the curve.
> Graph the three functions y = xa, y = ax, and y = logax on the same screen for two or three values of a > 1. For large values of x, which of these functions has the largest values and which has the smallest values?
> If f (x) = x2 -2x + 3, evaluate the difference quotient f (a + h) – f (a)/ h.
> The population of a certain species in a limited environment with initial population 100 and carrying capacity 1000 is where is measured in years. P (t) = 100,000/100 + 900e-t (a). Graph this function and estimate how long it takes for the population to
> The half-life of palladium-100, 100Pd, is four days. (So, half of any given quantity of 100Pd will disintegrate in four days.) The initial mass of a sample is one gram. (a). Find the mass that remains after 16 days. (b). Find the mass m (t) that remains
> Solve each equation for x. (a). ex = 5 (b). ln x = 2 (c). eex = 2
> Make a rough sketch of the graph of the function. Do not use a calculator. Just use the graphs given in Figures 3 and 13 and, if necessary, the transformations of Section 1.3. Figures 3: Figures 13: y = 1 – 1/2 e-x y4 10 4" 1.5
> Find the exact value of each expression. (a). e2ln3 (b). log 1025 + log104
> Find the inverse function of f (x) = x + 1/2x + 1.
> If f (x) = 2x + ln x, find f-1 (2).
> Express the function F (x) = 1 /√x + √x as a composition of three functions.
> If f (x) = ln x and g (x) = x2 - 9, find the functions (a) f0g, (b) g0f, (c) f0f, (d) g0g, and their domains.
> Use transformations to sketch the graph of the function. if x<0 f(x) = ez – 1 if x> 0
> Use transformations to sketch the graph of the function. f (x) = 1/ x + 2
> Use transformations to sketch the graph of the function. y = 2 - √x
> Use transformations to sketch the graph of the function. y = 1/2 (1 + ex)
> Use transformations to sketch the graph of the function. y = 3 ln (x – 2)
> Give an example of each type of function. (a). Linear function (b). Power function (c). Exponential function (d). Quadratic function (e). Polynomial of degree 5 (f). Rational function
> Discuss four ways of representing a function. Illustrate your discussion with examples.
> How to make an article, in Word with columns and pictures.

