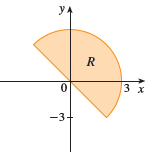
Question: A region R is shown. Decide whether
A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write∬R f (x, y) dA as an iterated integral, where f is an arbitrary continuous function on R.
Transcribed Image Text:
y. 3 х -3+
> Use polar coordinates to combine the sum into one double integral. Then evaluate the double integral. Sa l ty dy dx + ftvdy dx + 4-x2 xy dy dx ху.
> Calculate the iterated integral ∫_0^1 ∫_1^2(x+e^(-y) dx dy
> (a). Newton’s method for approximating a root of an equation f (x) = 0 (see Section 4.8) can be adapted to approximating a solution of a system of equations f (x, y) = 0 and g (x, y) = 0. The surfaces z = f (x, y) and z = t (x, y) inter
> Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y) %3 ху; 4х? + y? %3D 8 = 8
> Express the double integral in terms of a single integral with respect to r. Then use your calculator to evaluate the integral correct to four decimal places. ∬D e^(x^2+y^2 )^2 dA, where D is the disk with center the origin and radius 1
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^2 ∫_0^(√(2x-x^2 ) √(x^2+y^2 ) dy dx
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^(1/2) ∫_(√3 y)^(√(1-y^2 ) xy^2 dx dy
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^a ∫_(-√(a^2-y^2 ))^(√(a^2-y^2 ) (2x + y) dx dy
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 1 < x < 3, 1 < y < 4}; ρ (x, y) = ky2
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^2 ∫_0^(√(4-x^2 ) e^(-x^2-y^2 ) dy dx
> Find the volume of the given solid. Bounded by the planes z = x, y = x, x + y = 2, and z = 0
> Use polar coordinates to find the volume of the given solid. Inside both the cylinder x2 + y2 = 4 and the ellipsoid 4x2 + 4y2 + z2 = 64
> Use a computer algebra system to find the mass, center of mass, and moments of inertia of the lamina that occupies the region D and has the given density function. D is enclosed by the right loop of the four-leaved rose r = cos 2θ; θ (x, y) = x2 + y2
> (a). Find the maximum value of f (x1, x2, . . . , xn) = √(n&x_1 x_2…x_n ) given that x1, x2, . . ., xn are positive numbers and x1 + x2 + ∙ ∙ ∙ + xn = c, wher
> If you attempt to use Formula 2 to find the area of the top half of the sphere x2 + y2 + z2 = a2, you have a slight problem because the double integral is improper. In fact, the integrand has an infinite discontinuity at every point of the boundary circl
> Show that the area of the part of the plane z = ax + by + c that projects onto a region D in the xy-plane with area A (D) is √(a^2 + b^2 + 1) A (D).
> Find the area of the surface. The part of the plane 6x + 4y + 2z = 1 that lies inside the cylinder x2 + y2 = 25
> Find the exact area of the surface z = 1 + x + y + x2 -2 < x < 1 -1 < y < 1 Illustrate by graphing the surface.
> Find the exact area of the surface z = 1 + 2x + 3y + 4y2, 1 < x < 4, 0 < y < 1.
> (a). Use the Midpoint Rule for double integrals (see Section 15.1) with four squares to estimate the surface area of the portion of the paraboloid z = x2 + y2 that lies above the square [0, 1] × [0, 1]. (b). Use a computer algebra system to approximate t
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = cos (x2 + y2) that lies inside the cylinder x2 + y2 = 1
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = 1/ (1 + x2 + y2) that lies above the disk x2 + y2 < 1
> Find the maximum and minimum values of f subject to the given constraints. Use a computer algebra system to solve the system of equations that arises in using Lagrange multipliers. (If your CAS finds only one solution, you may need to use additional comm
> Find the center of mass of the lamina in Exercise 11 if the density at any point is proportional to the square of its distance from the origin. Exercise 11: A lamina occupies the part of the disk x2 + y2 < 1 in the first quadrant. Find its center of ma
> Find the area of the surface. The part of the sphere x2 + y2 + z2 = a2 that lies within the cylinder x2 + y2 = ax and above the xy-plane
> Find the area of the surface. The part of the sphere x2 + y2 + z2 = 4 that lies above the plane z = 1
> Find the area of the surface. The part of the plane 5x + 3y = z + 6 = 0 that lies above the rectangle [1, 4] × [2, 6]
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by the curves y = e-x, y = 0, x = 0, x = 1; ρ (x, y) = xy
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by y = x + 2 and y = x2; ρ (x, y) = kx2
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by y = 1 - x2 and y − 0; ρ (x, y) = ky
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is the triangular region enclosed by the lines y = 0, y = 2x, and x + 2y = 1; ρ (x, y) = x
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 0 < x < a, 0 < y < b}; ρ (x, y) = 1 + x2 + y2
> Find the maximum and minimum values of f subject to the given constraints. Use a computer algebra system to solve the system of equations that arises in using Lagrange multipliers. (If your CAS finds only one solution, you may need to use additional comm
> Use polar coordinates to find the volume of the given solid. Below the cone z = √(x^2 + y^2 ) and above the ring 1 < x2 + y2 < 4
> Electric charge is distributed over the disk x2 + y2 < 1 so that the charge density at (x, y) is (x, y) = √(x^2 + y^2 ) (measured in coulombs per square meter). Find the total charge on the disk.
> Use polar coordinates to find the volume of the given solid. Under the paraboloid z = x2 + y2 and above the disk x2 + y2 < 25
> Find the moments of inertia Ix, Iy, I0 for the lamina of Exercise 6. Exercise 6: Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is the triangular region enclosed by the lines y = 0, y =
> Find the moments of inertia Ix, Iy, I0 for the lamina of Exercise 3. Exercise 3: Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 1 < x < 3, 1 < y < 4}; ρ (x, y) = ky2
> A lamina occupies the region inside the circle x2 + y2 = 2y but outside the circle x2 + y2 = 1. Find the center of mass if the density at any point is inversely proportional to its distance from the origin.
> Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length a if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse.
> Find the center of mass of the lamina in Exercise 13 if the density at any point is inversely proportional to its distance from the origin. Exercise 13: The boundary of a lamina consists of the semicircles y = √(1 - x^2 ) and y = √(4 - x^2 ) together w
> The boundary of a lamina consists of the semicircles y = √(1 - x^2 ) and y = √(4 - x^2 ) together with the portions of the x-axis that join them. Find the center of mass of the lamina if the density at any point is proportional to its distance from the o
> The plane 4x - 3y + 8z = 5 intersects the cone z2 = x2 + y2 in an ellipse. (a). Graph the cone and the plane, and observe the elliptical intersection. (b). Use Lagrange multipliers to find the highest and lowest points on the ellipse.
> A lamina occupies the part of the disk x2 + y2 < 1 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is enclosed by the curves y = 0 and y = cos x, -π/2 < x < π/2; ρ (x, y) = y
> Evaluate the given integral by changing to polar coordinates. ∬R sin (x2 + y2) dA, where R is the region in the first quadrant between the circles with center the origin and radii 1 and 3.
> Evaluate the given integral by changing to polar coordinates. ∬R (2x – y) dA, where R is the region in the first quadrant enclosed by the circle x2 + y2 = 4 and the lines x = 0 and y = x
> Evaluate the given integral by changing to polar coordinates. ∬D x2y dA, where D is the top half of the disk with center the origin and radius 5.
> Evaluate the iterated integral. ∫_0^1 ∫_0^(e^y) √(1+e^y) dw dv
> A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write ∬R f (x, y) dA as an iterated integral, where f is an arbitrary continuous function on R. yA -1 1 R -1
> The plane x + y + 2z = 2 intersects the paraboloid z = x2 + y2 in an ellipse. Find the points on this ellipse that are nearest to and farthest from the origin.
> Use polar coordinates to find the volume of the given solid. Bounded by the paraboloids z = 6 - x2 - y2 and z = 2x2 + 2y2
> Use polar coordinates to find the volume of the given solid. Above the cone z = √(x^2 + y^2 ) and below the sphere x2 + y2 + z2 = 1
> Use polar coordinates to find the volume of the given solid. Bounded by the paraboloid z = 1 + 2x2 + 2y2 and the plane z = 7 in the first octant
> Use polar coordinates to find the volume of the given solid. A sphere of radius a
> Use polar coordinates to find the volume of the given solid. Inside the sphere x2 + y2 + z2 = 16 and outside the cylinder x2 + y2 = 4
> Use polar coordinates to find the volume of the given solid. Below the plane 2x + y + z = 4 and above the disk x2 + y2 < 1
> A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write ∬R f (x, y) dA as an iterated integral, where f is an arbitrary continuous function on R. y. 1 R -1 1 x
> Evaluate the double integral. ∬D (x2 + 2y) dA, D is bounded by y = x, y = x3, x > 0
> Evaluate the double integral. ∬D x cos y dA, D is bounded by y = 0, y = x2, x = 1
> Calculate the iterated integral ∫_0^1 ∫_0^1 (x+y)^2 dx dy
> Find the maximum and minimum volumes of a rectangular box whose surface area is 1500 cm2 and whose total edge length is 200 cm.
> Calculate the iterated integral ∫_1^4 ∫_0^2 (6x^2 y - 2x) dy dx
> Evaluate the given integral by changing to polar coordinates. ∬D x dA, where D is the region in the first quadrant that lies between the circles x2 + y2 = 4 and x2 + y2 = 2x
> Find ∫_0^2 f (x,y) dx and ∫_0^3 f(x,y) dy f (x, y) = x + 3x2y2
> Evaluate the given integral by changing to polar coordinates. ∬R cos √(x^2 + y^2 ) dA, where D is the disk with center the origin and radius 2
> Evaluate the given integral by changing to polar coordinates. ∬D e^(-x^2-y^2 ) dA, where D is the region bounded by the semicircle x = √(4 - y^2 ) and the y-axis.
> Evaluate the given integral by changing to polar coordinates. ∬R y^2/(x^2 + y^2 ) dA, where R is the region that lies between the circles x2 + y2 = a2 and x2 + y2 = b2 with 0 < a < b
> A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write ∬R f (x, y) dA as an iterated integral, where f is an arbitrary continuous function on R. T5 R 2 5 2.
> Evaluate the double integral. ∬D e^(-y^2 ) dA, D = {(x, y) | 0 < y < 3, 0 < x < y}
> Evaluate the double integral. ∬D (2x + y) dA, D = {(x, y) | 1 < y < 2, y - 1 < x < 1}
> Use Lagrange multipliers to give an alternate solution to the indicated exercise in Section 14.7. Exercise 55 14.7 Exercise 55: If the length of the diagonal of a rectangular box must be L, what is the largest possible volume?
> Evaluate the iterated integral. ∫_0^1 ∫_0^(x^2)cos (s^3) dt ds
> Use a computer algebra system to find the exact volume of the solid. Under the surface z = x3y4 + xy2 and above the region bounded by the curves y = x3 - x and y = x2 + x for x > 0
> Sketch the solid whose volume is given by the iterated integral. ∫_0^1 ∫_0^(1-x^2) (1 - x) dy dx
> Evaluate the iterated integral. ∫_0^(π/2) ∫_0^x〖(x siny)〗dy dx
> Find the volume of the solid lying under the elliptic paraboloid x2/4 + y2/9 + z = 1 and above the rectangle R = [-1, 1] × [-2, 2].
> Find the volume of the solid by subtracting two volumes. The solid in the first octant under the plane z = x + y, above the surface z = xy, and enclosed by the surfaces x = 0, y = 0, and x2 + y2 = 4
> Calculate the double integral. ∬R 1/(1+ x+ y) dA, R = [1, 3] × [1, 2]
> Use a graphing calculator or computer to estimate the x-coordinates of the points of intersection of the curves y = x4 and y = 3x - x2. If D is the region bounded by these curves, estimate ∬D x dA.
> Find the volume of the given solid. Bounded by the cylinders x2 + y2 = r2 and y2 + z2 = r2
> Find the volume of the given solid. Bounded by the cylinder x2 + y2 = 1 and the planes y = z, x = 0, z = 0 in the first octant
> Use Lagrange multipliers to give an alternate solution to the indicated exercise in Section 14.7. Exercise 52 14.7 Exercise 52: The base of an aquarium with given volume V is made of slate and the sides are made of glass. If slate costs five times as m
> Find the volume of the given solid. Bounded by the cylinder y2 + z2 = 4 and the planes x − 2y, x = 0, z = 0 in the first octant
> Evaluate the iterated integral. ∫_0^1 ∫_0^y (〖xe〗^(y^3 ) dx dy
> Find the volume of the given solid. Enclosed by the cylinders z = x2, y = x2 and the planes z = 0, y = 4
> Find the volume of the given solid. The tetrahedron enclosed by the coordinate planes and the plane 2x + y + z = 4
> Find the volume of the given solid. Enclosed by the paraboloid z = x2 + y2 + 1 and the planes x = 0, y = 0, z = 0, and x + y = 2
> Find the volume of the given solid. Under the surface z = xy and above the triangle with vertices (1, 1), (4, 1), and (1, 2)
> Find the volume of the given solid. Under the surface z = 1 + x2y2 and above the region enclosed by x = y2 and x = 4
> Find the volume of the given solid. Under the plane 3x + 2y - z = 0 and above the region enclosed by the parabolas y = x2 and x = y2
> Evaluate the double integral. ∬D y dA, D is the triangular region with vertices (0, 0), (1, 1), and (4, 0)
> Use Lagrange multipliers to give an alternate solution to the indicated exercise in Section 14.7. Exercise 51 14.7 Exercise 51: Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is a constant c.
> Evaluate the double integral. ∬D y2 dA, D is enclosed by the quarter-circle y = √(1 -x^2 ), x > 0, and the axes
> Evaluate the iterated integral. ∫_0^2 ∫_0^2(x^2 y dx dy
> Evaluate the double integral. ∬D y2 dA, D is the triangular region with vertices (0, 1), (1, 2), (4, 1)
> Find ∫_0^2 f (x,y) dx and ∫_0^3 f(x,y) dy f (x, y) = y√(x + 2)
> The integral ∬R √(9 - y^2 ) dA, where R = [0, 4] × [0, 2], represents the volume of a solid. Sketch the solid.
> (a). Estimate the volume of the solid that lies below the surface z = xy and above the rectangle R = {(x, y) | 0 < x < 6, 0 < y < 4} Use a Riemann sum with m = 3, n = 2, and take the sample point to be the upper right corner of each square. (b). Use th
> Evaluate the double integral. ∬D y √(x^2- y^2 ) dA, D = {(x, y) | 0 < x < 2, 0 < y < x}

