Question:
(a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis.
(b) Use your calculator to evaluate the integral correct to five decimal places.
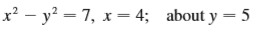
Transcribed Image Text:
x? – y? = 7, x = 4; about y = 5
> Suppose that for the tank in Exercise 23 the pump breaks down after 4.7 × 105 J of work has been done. What is the depth of the water remaining in the tank? Data from Exercise 23: A tank is full of water. Find the work required to pump the
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 25 and 26 use the fact that water weighs 62.5 lb/ft3. 6 ft 26. 12 ft - f 8 ft 6 ft - 3 ft 10 ft frustum of a cone
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 25 and 26 use the fact that water weighs 62.5 lb/ft3. - 3 m - 24. |1 m 2 m 3 m 3 m 8 m
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A spherical water tank, 24 ft in diameter, sits atop a 60 ft tower. The tank is filled by a hose attached to the bottom of the sphere. If a
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. An aquarium 2 m long, 1 m wide, and 1 m deep is full of water. Find the work needed to pump half of the water out of the aquarium. (Use the
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A circular swimming pool has a diameter of 24 ft, the sides are 5 ft high, and the depth of the water is 4 ft. How much work is required to
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A 10-ft chain weighs 25 lb and hangs from a ceiling. Find the work done in lifting the lower end of the chain to the ceiling so that it’s le
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A bucket that weighs 4 lb and a rope of negligible weight are used to draw water from a well that is 80 ft deep. The bucket is filled with 4
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A leaky 10-kg bucket is lifted from the ground to a height of 12 m at a constant speed with a rope that weighs 0.8 kg/m. Initially the bucke
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A chain lying on the ground is 10 m long and its mass is 80 kg. How much work is required to raise one end of the chain to a height of 6 m?
> Sketch the region enclosed by the given curves and find its area. х — у, у— V2 — х, у— 0 2- х, у x =
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A cable that weighs 2 lb/ft is used to lift 800 lb of coal up a mine shaft 500 ft deep. Find the work done.
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A thick cable, 60 ft long and weighing 180 lb, hangs from a winch on a crane. Compute in two different ways the work done if the winch winds
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A heavy rope, 50 ft long, weighs 0.5 lb/ft and hangs over the edge of a building 120 ft high. (a) How much work is done in pulling the rope
> If 6 J of work is needed to stretch a spring from 10 cm to 12 cm and another 10 J is needed to stretch it from 12 cm to 14 cm, what is the natural length of the spring?
> A spring has natural length 20 cm. Compare the work W1 done in stretching the spring from 20 cm to 30 cm with the work W2 done in stretching it from 30 cm to 40 cm. How are W2 and W1 related?
> If the work required to stretch a spring 1 ft beyond its natural length is 12 ft-lb, how much work is needed to stretch it 9 in. beyond its natural length?
> Suppose that 2 J of work is needed to stretch a spring from its natural length of 30 cm to a length of 42 cm. (a) How much work is needed to stretch the spring from 35 cm to 40 cm? (b) How far beyond its natural length will a force of 30 N keep the sprin
> A spring has a natural length of 40 cm. If a 60-N force is required to keep the spring compressed 10 cm, how much work is done during this compression? How much work is required to compress the spring to a length of 25 cm?
> A force of 10 lb is required to hold a spring stretched 4 in. beyond its natural length. How much work is done in stretching it from its natural length to 6 in. beyond its natural length?
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. -у — х*, у— 0, х— 1, х— 2
> Sketch the region enclosed by the given curves and find its area. у — сos пх, у— 4x? — 1 y = 4x² – 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — Vх, у— 0, х—1
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its circumference and height. Use shells to find the volume of S. Do you think this method is preferable to slicing? Expl
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Explain why it is awkward to use slicing to find the volume V of S. Sketch a typical approximating shell. What are its circumference and height? Use shells to find V
> Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters). You discover that both napkin rings have the same height h, as shown in the figure. (a) Guess which ring has more woo
> Use cylindrical shells to find the volume of the solid. A right circular cone with height h and base radius r
> Use cylindrical shells to find the volume of the solid. The solid torus of Exercise 6.2.63 Data from Exercise 6.2: Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its
> Use cylindrical shells to find the volume of the solid. A sphere of radius r
> Let T be the triangular region with vertices (0, 0), (1, 0), and (1, 2), and let V be the volume of the solid generated when T is rotated about the line x = a, where a > 1. Express a in terms of V.
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. = X х — (у — 1), х — у — 1; aboutx — -1
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x = (y – 3)', x = 4; about y = 1
> Sketch the region enclosed by the given curves and find its area. y = у — Vx — 1, х — у— 1 y
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x? + (y – 1) = 1; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x² = 1, y = 2; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x? = 1, y = 2; about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у 3 —х? + 6х — 8, у — 0;B about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у — —х? + 6х - 8, у — 0;B about the y-axis
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x'sin x, y = 0, 0 <x< T; about x = -1
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = sin?x, y = sin*x, 0 < x< T; about x = T/2
> Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the y-axis the region enclosed by these curves.
> Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the y-axis the region enclosed by these curves.
> Each integral represents the volume of a solid. Describe the solid. 27 (2 – x)(3* 2*) dx
> Sketch the region enclosed by the given curves and find its area. x = 2y?, x= 4 + y?
> Each integral represents the volume of a solid. Describe the solid. * y + 2 dy y?
> Each integral represents the volume of a solid. Describe the solid. 2ту Iny dy
> Each integral represents the volume of a solid. Describe the solid. | 2nx° dx
> If the region shown in the figure is rotated about the y-axis to form a solid, use the Midpoint Rule with n = 5 to estimate the volume of the solid. y 4 4 6 8 10 x 2. 2.
> Use the Midpoint Rule with n = 5 to estimate the volume obtained by rotating about the y-axis the region under the curve /
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. Vsin y, 0 < y < T, x = 0; about y
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. y = x, y= 2x/(1 + x³); about x =
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у — сos'x, у — —-cos'x, —п/2 <х <
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у 3 tan x, у — 0, х — п/4; аbout
> Sketch the region enclosed by the given curves and find its area. y = cos x, y=2 – cos x, 0<x<2n
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у — хе ", у — 0, х — 2;B about th
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. x = 2y², x = y² + 1; about y = -2
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. x = 2y?, y > 0, x= 2; about y = 2
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = Vx, x = 2y; about x = 5
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = 4x – x', y = 3; about x = 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. у 3 4 — 2х, у — 0, х — 0; аbout x — —1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = x', y = 8, x = 0; about x = 3
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. х+у — 4, х— у? — x + 4y + 4 =
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = 1 + (y – 2)?, x= 2
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = - Зу? + 12у — x = 0
> Sketch the region enclosed by the given curves and find its area. у3D sec*x, у—8 cos х, -T/3 < x< m/3
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y = у — хУ, у — 8, х— 0 -3/2 у 3 8, х— 0 y
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. у — х, х— 0, у-2
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. ху — 1, х— 0, у —1, у—3
> Let V be the volume of the solid obtained by rotating about the y-axis the region bounded by / Find V both by slicing and by cylindrical shells. In both cases draw a diagram to explain your method.
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — х?, у—6х — 2х? y y
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — 4х — х*, у — х y y =x
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. y =e *? у —е*, у—0, х—0, х—1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. х— 2Vy, х — 0, у — 9;B about the y-аxis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —е", у — 0, х— —1, х— 1; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — Vx — 1, у — 0, х — 5; about the x-axis
> Sketch the region enclosed by the given curves and find its area. y = x', y= 4x – x²
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — 1/х, у — 0, х— 1, х — 4; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —х+ 1, у— 0, х — 0, х — 2; about the x-axis
> Find the volume of the described solid S. The solid S is bounded by circles that are perpendicular to the x-axis, intersect the x-axis, and have centers on the parabola / e/
> Find the volume of the described solid S. The base of S is the region enclosed by y = 2 - x2 and the x-axis. Cross-sections perpendicular to the y-axis are quarter-circles. y=2-x?
> Find the volume of the described solid S. The base of S is the same base as in Exercise 58, but cross sections perpendicular to the x-axis are isosceles triangles with height equal to the base.
> Find the volume of the described solid S. The base of S is the region enclosed by the parabola y = 1 - x2 and the x-axis. Cross-sections perpendicular to the y-axis are squares.
> Find the volume of the described solid S. The base of S is the same base as in Exercise 56, but cross sections perpendicular to the x-axis are squares. Data from Exercise 56: Find the volume of the described solid S. The base of S is the triangular reg
> Find the volume of the described solid S. The base of S is the triangular region with vertices (0, 0), (1, 0), and (0, 1). Cross-sections perpendicular to the y-axis are equilateral triangles.
> Find the volume of the described solid S. The base of S is an elliptical region with boundary curve 9x2 + 4y2 = 36. Cross-sections perpendicular to the x-axis are isosceles right triangles with hypotenuse in the base.
> Find the volume of the described solid S. The base of S is a circular disk with radius r. Parallel cross sections perpendicular to the base are squares.
> Sketch the region enclosed by the given curves and find its area. у — 12 — х?, у — х? — 6 y
> Find the volume of the described solid S. A tetrahedron with three mutually perpendicular faces and three mutually perpendicular edges with lengths 3 cm, 4 cm, and 5 cm
> Find the volume of the described solid S. a a a
> Find the volume of the described solid S. A pyramid with height h and rectangular base with dimensions b and 2b
> Find the volume of the described solid S. A frustum of a pyramid with square base of side b, square top of side a, and height h What happens if a = b? What happens if a = 0? a
> Find the volume of the described solid S. A cap of a sphere with radius r and height h
> Find the volume of the described solid S. A frustum of a right circular cone with height h, lower base radius R, and top radius r ード ーミー
> Find the volume of the described solid S. A right circular cone with height h and base radius r
> (a) A model for the shape of a bird’s egg is obtained by rotating about the x-axis the region under the graph of Use a CAS to find the volume of such an egg. (b) For a red-throated loon, a = 20.06, b = 0.04, c = 0.1, and d = 0.54. Graph
> (a) If the region shown in the figure is rotated about the x-axis to form a solid, use the Midpoint Rule with n = 4 to estimate the volume of the solid. (b) Estimate the volume if the region is rotated about the y-axis. Again use the Midpoint Rule wit
> A log 10 m long is cut at 1-meter intervals and its cross- sectional areas A (at a distance x from the end of the log) are listed in the table. Use the Midpoint Rule with n = 5 to estimate the volume of the log. x (m) A (m²) x (m) A (m²) 0.68 0.53 1
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. 4х + у? — 12, х—у
> A CAT scan produces equally spaced cross-sectional views of a human organ that provide information about the organ otherwise obtained only by surgery. Suppose that a CAT scan of a human liver shows cross-sections spaced 1.5 cm apart. The liver is 15 cm l
> Each integral represents the volume of a solid. Describe the solid.

