Question: Use the method of cylindrical shells to
Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis.
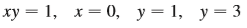
Transcribed Image Text:
ху — 1, х— 0, у —1, у—3
> A force of 10 lb is required to hold a spring stretched 4 in. beyond its natural length. How much work is done in stretching it from its natural length to 6 in. beyond its natural length?
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. -у — х*, у— 0, х— 1, х— 2
> Sketch the region enclosed by the given curves and find its area. у — сos пх, у— 4x? — 1 y = 4x² – 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — Vх, у— 0, х—1
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its circumference and height. Use shells to find the volume of S. Do you think this method is preferable to slicing? Expl
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Explain why it is awkward to use slicing to find the volume V of S. Sketch a typical approximating shell. What are its circumference and height? Use shells to find V
> Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters). You discover that both napkin rings have the same height h, as shown in the figure. (a) Guess which ring has more woo
> Use cylindrical shells to find the volume of the solid. A right circular cone with height h and base radius r
> Use cylindrical shells to find the volume of the solid. The solid torus of Exercise 6.2.63 Data from Exercise 6.2: Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its
> Use cylindrical shells to find the volume of the solid. A sphere of radius r
> Let T be the triangular region with vertices (0, 0), (1, 0), and (1, 2), and let V be the volume of the solid generated when T is rotated about the line x = a, where a > 1. Express a in terms of V.
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. = X х — (у — 1), х — у — 1; aboutx — -1
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x = (y – 3)', x = 4; about y = 1
> Sketch the region enclosed by the given curves and find its area. y = у — Vx — 1, х — у— 1 y
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x? + (y – 1) = 1; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x² = 1, y = 2; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x? = 1, y = 2; about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у 3 —х? + 6х — 8, у — 0;B about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у — —х? + 6х - 8, у — 0;B about the y-axis
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x'sin x, y = 0, 0 <x< T; about x = -1
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = sin?x, y = sin*x, 0 < x< T; about x = T/2
> Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the y-axis the region enclosed by these curves.
> Use a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information and your calculator to estimate the volume of the solid obtained by rotating about the y-axis the region enclosed by these curves.
> Each integral represents the volume of a solid. Describe the solid. 27 (2 – x)(3* 2*) dx
> Sketch the region enclosed by the given curves and find its area. x = 2y?, x= 4 + y?
> Each integral represents the volume of a solid. Describe the solid. * y + 2 dy y?
> Each integral represents the volume of a solid. Describe the solid. 2ту Iny dy
> Each integral represents the volume of a solid. Describe the solid. | 2nx° dx
> If the region shown in the figure is rotated about the y-axis to form a solid, use the Midpoint Rule with n = 5 to estimate the volume of the solid. y 4 4 6 8 10 x 2. 2.
> Use the Midpoint Rule with n = 5 to estimate the volume obtained by rotating about the y-axis the region under the curve /
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. x? – y? = 7, x = 4; about y = 5
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. Vsin y, 0 < y < T, x = 0; about y
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. y = x, y= 2x/(1 + x³); about x =
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у — сos'x, у — —-cos'x, —п/2 <х <
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у 3 tan x, у — 0, х — п/4; аbout
> Sketch the region enclosed by the given curves and find its area. y = cos x, y=2 – cos x, 0<x<2n
> (a) Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curve about the specified axis. (b) Use your calculator to evaluate the integral correct to five decimal places. у — хе ", у — 0, х — 2;B about th
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. x = 2y², x = y² + 1; about y = -2
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. x = 2y?, y > 0, x= 2; about y = 2
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = Vx, x = 2y; about x = 5
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = 4x – x', y = 3; about x = 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. у 3 4 — 2х, у — 0, х — 0; аbout x — —1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the specified axis. y = x', y = 8, x = 0; about x = 3
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. х+у — 4, х— у? — x + 4y + 4 =
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = 1 + (y – 2)?, x= 2
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. x = - Зу? + 12у — x = 0
> Sketch the region enclosed by the given curves and find its area. у3D sec*x, у—8 cos х, -T/3 < x< m/3
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. y = у — хУ, у — 8, х— 0 -3/2 у 3 8, х— 0 y
> Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the given curves about the x-axis. у — х, х— 0, у-2
> Let V be the volume of the solid obtained by rotating about the y-axis the region bounded by / Find V both by slicing and by cylindrical shells. In both cases draw a diagram to explain your method.
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — х?, у—6х — 2х? y y
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — 4х — х*, у — х y y =x
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. y =e *? у —е*, у—0, х—0, х—1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. х— 2Vy, х — 0, у — 9;B about the y-аxis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —е", у — 0, х— —1, х— 1; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — Vx — 1, у — 0, х — 5; about the x-axis
> Sketch the region enclosed by the given curves and find its area. y = x', y= 4x – x²
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у — 1/х, у — 0, х— 1, х — 4; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у —х+ 1, у— 0, х — 0, х — 2; about the x-axis
> Find the volume of the described solid S. The solid S is bounded by circles that are perpendicular to the x-axis, intersect the x-axis, and have centers on the parabola / e/
> Find the volume of the described solid S. The base of S is the region enclosed by y = 2 - x2 and the x-axis. Cross-sections perpendicular to the y-axis are quarter-circles. y=2-x?
> Find the volume of the described solid S. The base of S is the same base as in Exercise 58, but cross sections perpendicular to the x-axis are isosceles triangles with height equal to the base.
> Find the volume of the described solid S. The base of S is the region enclosed by the parabola y = 1 - x2 and the x-axis. Cross-sections perpendicular to the y-axis are squares.
> Find the volume of the described solid S. The base of S is the same base as in Exercise 56, but cross sections perpendicular to the x-axis are squares. Data from Exercise 56: Find the volume of the described solid S. The base of S is the triangular reg
> Find the volume of the described solid S. The base of S is the triangular region with vertices (0, 0), (1, 0), and (0, 1). Cross-sections perpendicular to the y-axis are equilateral triangles.
> Find the volume of the described solid S. The base of S is an elliptical region with boundary curve 9x2 + 4y2 = 36. Cross-sections perpendicular to the x-axis are isosceles right triangles with hypotenuse in the base.
> Find the volume of the described solid S. The base of S is a circular disk with radius r. Parallel cross sections perpendicular to the base are squares.
> Sketch the region enclosed by the given curves and find its area. у — 12 — х?, у — х? — 6 y
> Find the volume of the described solid S. A tetrahedron with three mutually perpendicular faces and three mutually perpendicular edges with lengths 3 cm, 4 cm, and 5 cm
> Find the volume of the described solid S. a a a
> Find the volume of the described solid S. A pyramid with height h and rectangular base with dimensions b and 2b
> Find the volume of the described solid S. A frustum of a pyramid with square base of side b, square top of side a, and height h What happens if a = b? What happens if a = 0? a
> Find the volume of the described solid S. A cap of a sphere with radius r and height h
> Find the volume of the described solid S. A frustum of a right circular cone with height h, lower base radius R, and top radius r ード ーミー
> Find the volume of the described solid S. A right circular cone with height h and base radius r
> (a) A model for the shape of a bird’s egg is obtained by rotating about the x-axis the region under the graph of Use a CAS to find the volume of such an egg. (b) For a red-throated loon, a = 20.06, b = 0.04, c = 0.1, and d = 0.54. Graph
> (a) If the region shown in the figure is rotated about the x-axis to form a solid, use the Midpoint Rule with n = 4 to estimate the volume of the solid. (b) Estimate the volume if the region is rotated about the y-axis. Again use the Midpoint Rule wit
> A log 10 m long is cut at 1-meter intervals and its cross- sectional areas A (at a distance x from the end of the log) are listed in the table. Use the Midpoint Rule with n = 5 to estimate the volume of the log. x (m) A (m²) x (m) A (m²) 0.68 0.53 1
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. 4х + у? — 12, х—у
> A CAT scan produces equally spaced cross-sectional views of a human organ that provide information about the organ otherwise obtained only by surgery. Suppose that a CAT scan of a human liver shows cross-sections spaced 1.5 cm apart. The liver is 15 cm l
> Each integral represents the volume of a solid. Describe the solid.
> Each integral represents the volume of a solid. Describe the solid. " (o* – y") dy TT
> Each integral represents the volume of a solid. Describe the solid. "f', (1 – y°y° dy TT
> Each integral represents the volume of a solid. Describe the solid. [" sin x dx Jo
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y - x, y - xe' /2; about y = 3
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = sin?x, y = 0, 0 < x< ™; about y = -1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the x-axis the region bounded by these curves. у 31+
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the x-axis the region bounded by these curves. у — In
> Set up an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Then use your calculator to evaluate the integral correct to five decimal places. (a)
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. х —D1 - у?, х-- у? — 1
> Find the area of the shaded region. yA (1, е), y=e* y=xe**
> Compare a municipal bond with a tax-deferred annuity. When would one be more attractive than the other?
> Using the table in Example 14.13 on page 442 providing a comparison of tax- advantaged structures, explain why the qualified pension plan and the Roth IRA seem to be particularly attractive investments.
> Why is a qualified pension plan such an attractive tax shelter?
> Assuming that you didn’t regard a stock that declined since you bought it particularly highly, why wouldn’t you want to take a loss in the current year?
> Sarah had unrealized long-term capital gains and Marcy had unrealized long-term capital losses at year-end. When should each sell her shares: the current year or the next year?
> State how taxes are relevant in five major financial planning areas.
> When would a mutual fund be more attractive than an annuity?
> Which plan is more likely to be attractive to a younger person, a defined benefit or a defined contribution plan?
> Explain the difference between a defined benefit and a defined contribution plan.

